2 IV 60 Computer graphics set 4 3

2 IV 60 Computer graphics set 4: 3 D transformations and hierarchical modeling Jack van Wijk TU/e

From 2 D to 3 D • Much +/- the same: – Translation, scaling – Homogeneous vectors: one extra coordinate – Matrices: 4 x 4 • Rotation more complex

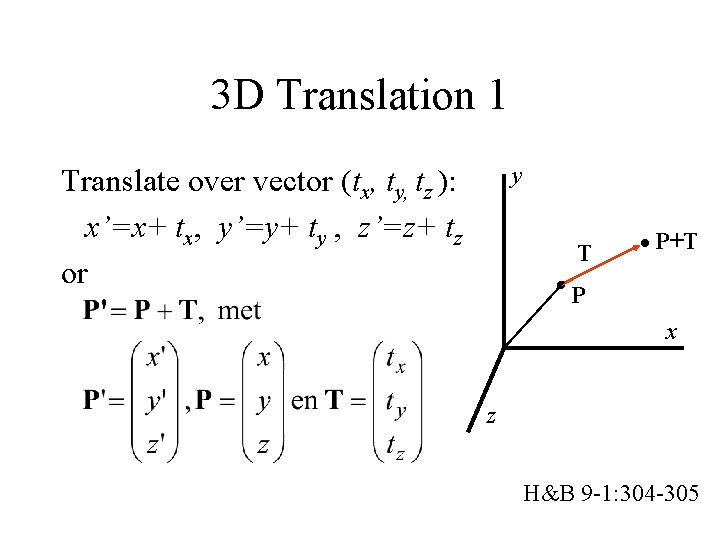
3 D Translation 1 y Translate over vector (tx, ty, tz ): x’=x+ tx, y’=y+ ty , z’=z+ tz or T P+T P x z H&B 9 -1: 304 -305

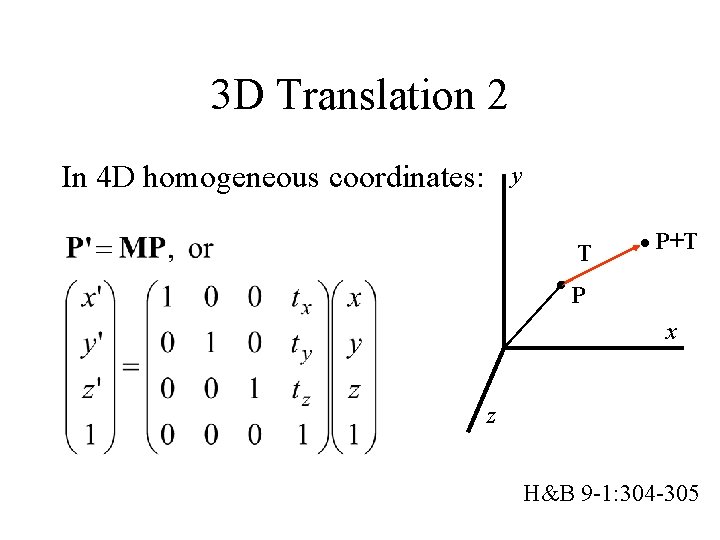
3 D Translation 2 In 4 D homogeneous coordinates: y T P+T P x z H&B 9 -1: 304 -305

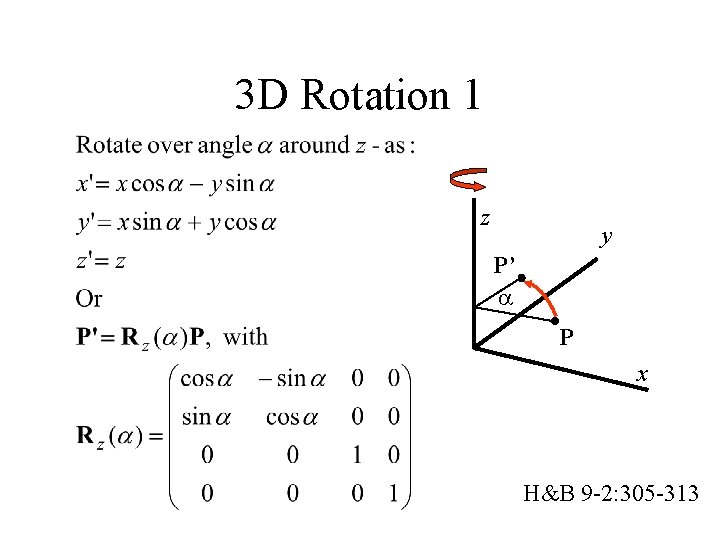
3 D Rotation 1 z y P’ P x H&B 9 -2: 305 -313

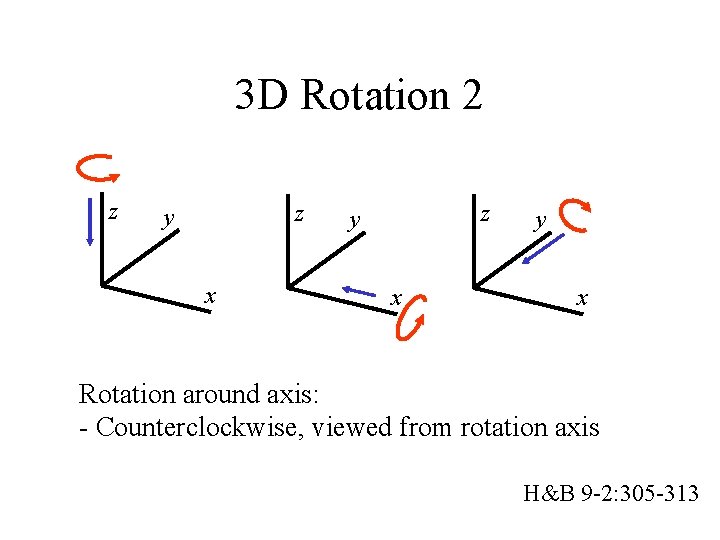
3 D Rotation 2 z z y x y x Rotation around axis: - Counterclockwise, viewed from rotation axis H&B 9 -2: 305 -313

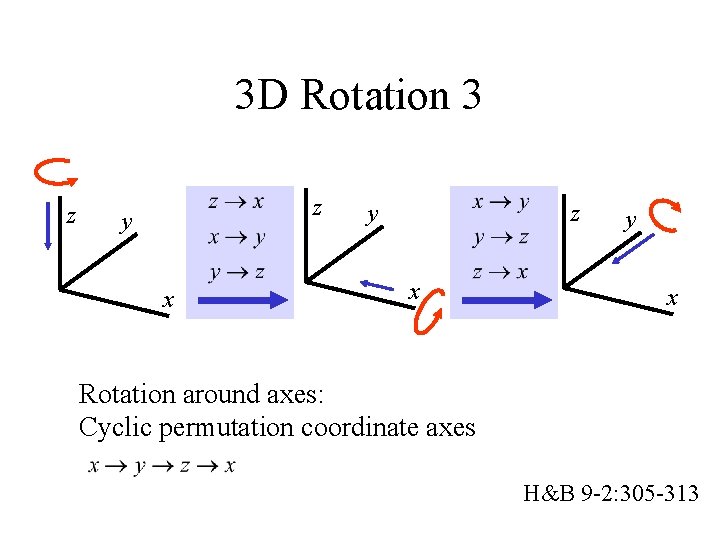
3 D Rotation 3 z z y x y z x y x Rotation around axes: Cyclic permutation coordinate axes H&B 9 -2: 305 -313

3 D Rotatie 4 H&B 9 -2: 305 -313

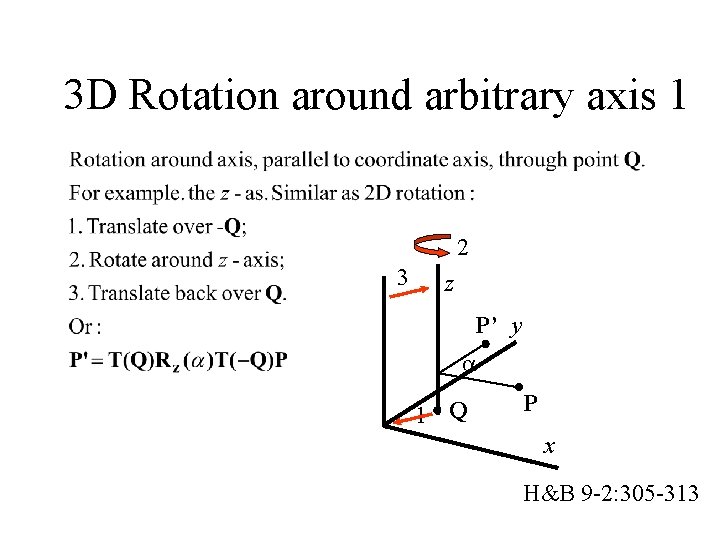
3 D Rotation around arbitrary axis 1 2 3 z P’ y 1 Q P x H&B 9 -2: 305 -313

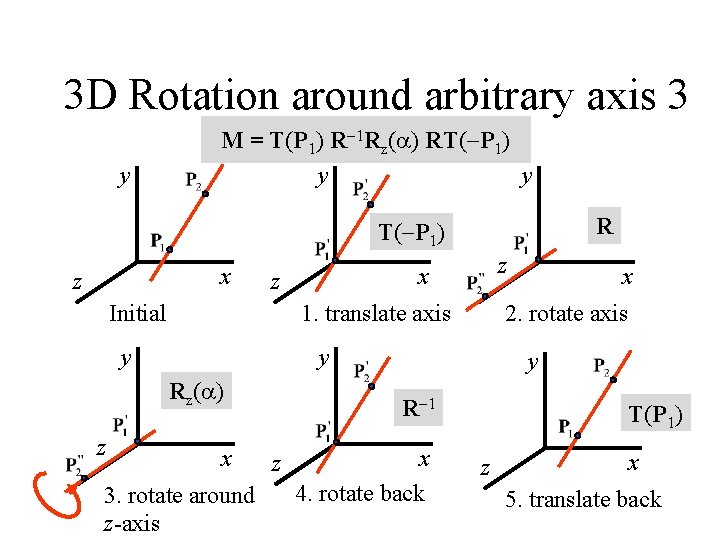
3 D Rotation around arbitrary axis 2 Rotation around axis through two points P 1 and P 1. More complex: 1. Translate such that axis goes through origin; 2. Rotate… 3. Translate back again. y z x H&B 9 -2: 305 -313

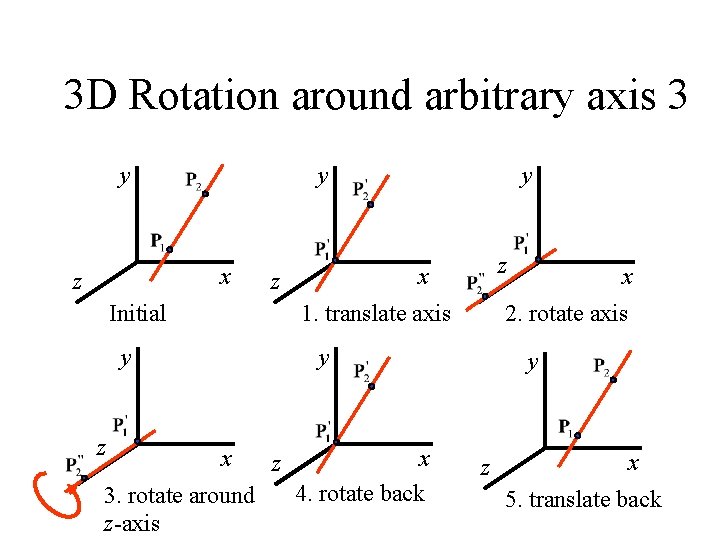
3 D Rotation around arbitrary axis 3 y y x z 1. translate axis y z z x z Initial y 2. rotate axis y x 3. rotate around z-axis z x 4. rotate back x y z x 5. translate back

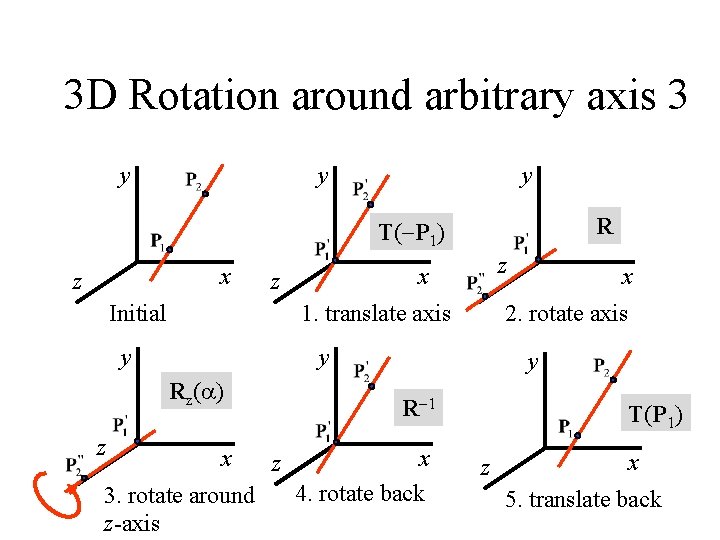
3 D Rotation around arbitrary axis 3 y y y R T( P 1) x z z Initial 1. translate axis y x 3. rotate around z-axis y R 1 z x 2. rotate axis y Rz( ) z z x x 4. rotate back T(P 1) z x 5. translate back

3 D Rotation around arbitrary axis 3 y M = T(P 1) R 1 Rz( ) RT( P 1) y y R T( P 1) x z z Initial 1. translate axis y x 3. rotate around z-axis y R 1 z x 2. rotate axis y Rz( ) z z x x 4. rotate back T(P 1) z x 5. translate back

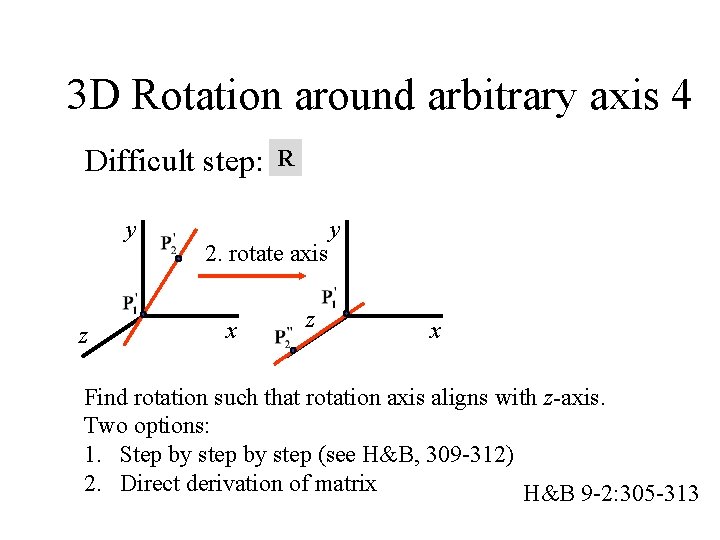
3 D Rotation around arbitrary axis 4 Difficult step: y z R 2. rotate axis x z y x Find rotation such that rotation axis aligns with z-axis. Two options: 1. Step by step (see H&B, 309 -312) 2. Direct derivation of matrix H&B 9 -2: 305 -313

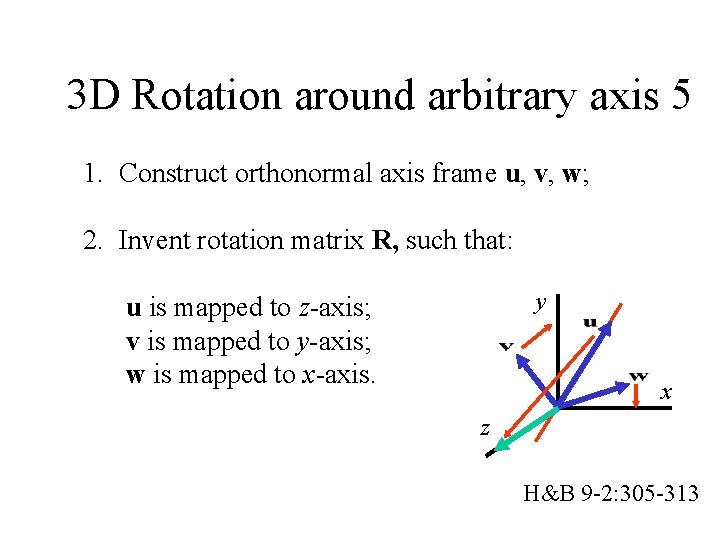
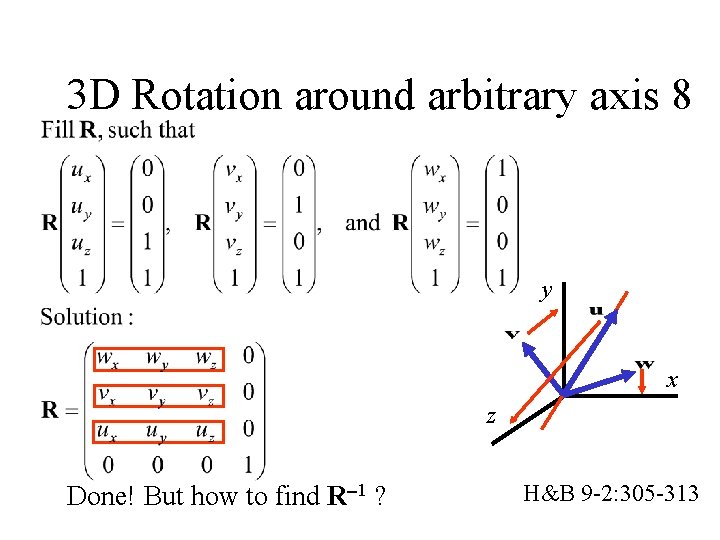
3 D Rotation around arbitrary axis 5 1. Construct orthonormal axis frame u, v, w; 2. Invent rotation matrix R, such that: y u is mapped to z-axis; v is mapped to y-axis; w is mapped to x-axis. x z H&B 9 -2: 305 -313

3 D Rotation around arbitrary axis 6 Construct orthonormal axis frame u, v, w: u = (P 2 P 1) / |P 2 P 1| v = u (1, 0, 0) / | u (1, 0, 0) | w=v u (If u = (a, 0, 0), then use (0, 1, 0)) y x This frame is orthonormal: z Unit length axes: u. u = v. v = w. w = 1 All axes perpendicular: u. v = v. w = w. u = 0 H&B 9 -2: 305 -313

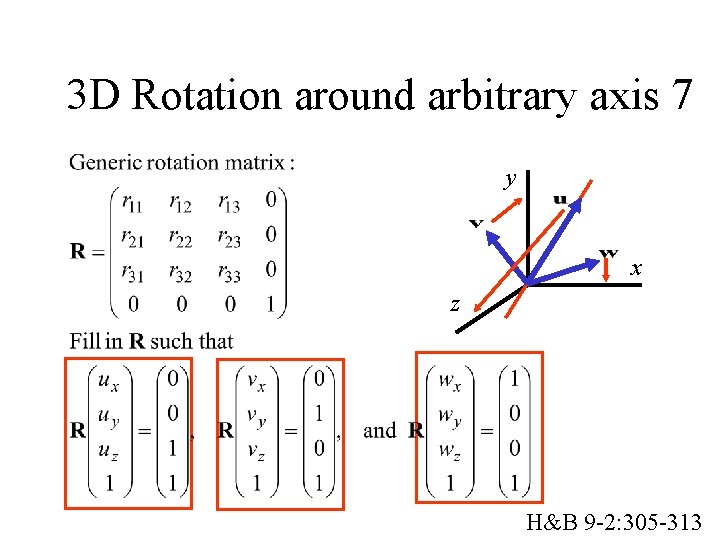
3 D Rotation around arbitrary axis 7 y x z H&B 9 -2: 305 -313

3 D Rotation around arbitrary axis 8 y x z Done! But how to find R 1 ? H&B 9 -2: 305 -313

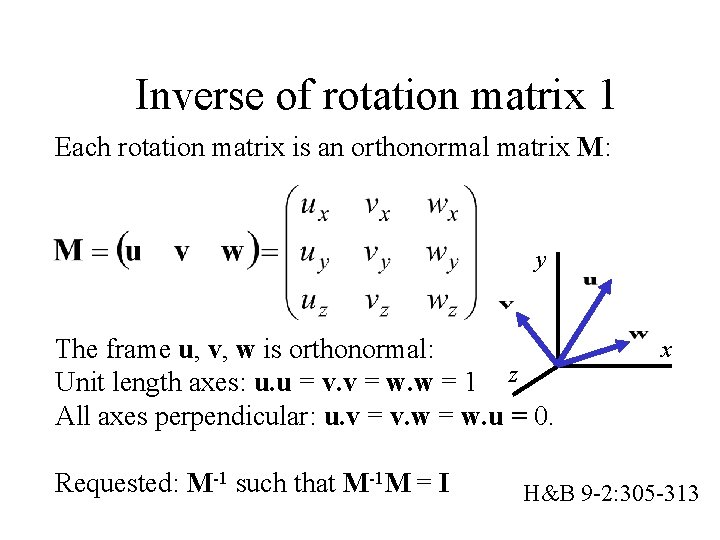
Inverse of rotation matrix 1 Each rotation matrix is an orthonormal matrix M: y The frame u, v, w is orthonormal: Unit length axes: u. u = v. v = w. w = 1 z All axes perpendicular: u. v = v. w = w. u = 0. Requested: M-1 such that M-1 M = I x H&B 9 -2: 305 -313

Inverse of rotation matrix 2 Requested: M-1 such that M-1 M = I Solution: In words: The inverse of a rotation matrix is the transpose. (For a rotation around the origin). H&B 9 -2: 305 -313

Inverse of rotation matrix 3 Requested: M-1 such that M-1 M = I Solution: M-1 = M-T Check: H&B 9 -2: 305 -313

3 D Rotation with quaternions Quaternions: • Extension of complex numbers • Four components • Scalar value + 3 D vector: q=(s, v) • Special calculation rules • Compact description of rotations • To be used if many complex rotations have to be done (esp. animation) H&B 9 -2: 313 -317

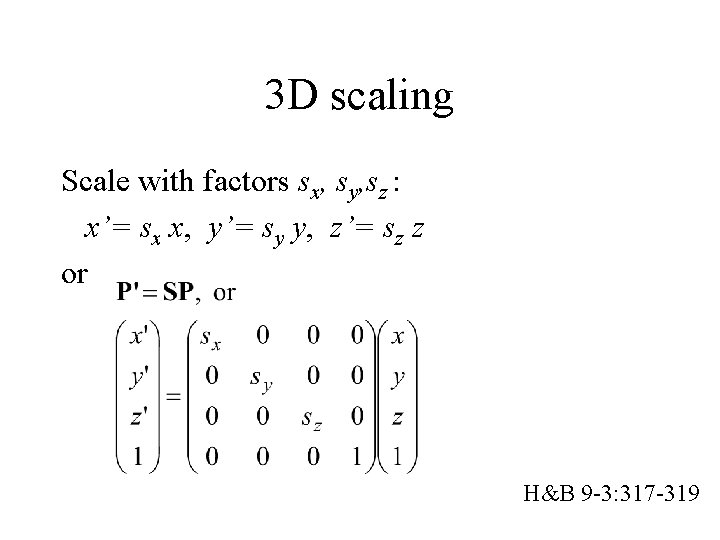
3 D scaling Scale with factors sx, sy, sz : x’= sx x, y’= sy y, z’= sz z or H&B 9 -3: 317 -319

More 3 D transformations +/- same as in 2 D: • • Matrix concatenation by multiplication Reflection Shearing Transformations between coordinate systems H&B 9 -4, 9 -5, 9 -6: 319 -324

Affine transformations 1 Generic name for these transformations: affine transformations H&B 9 -7: 324

Affine transformations 2 Properties: 1. Transformed coordinates x’, y’ and z’ are linearly dependent on original coordinates x, y en z. 2. Parameters aij en bk are constant and determine type of transformation; 3. Examples: translation, rotation, scaling, reflection 4. Parallel lines remain parallel 5. Only translation, rotation reflection: angles and lengths are maintained H&B 9 -7: 324

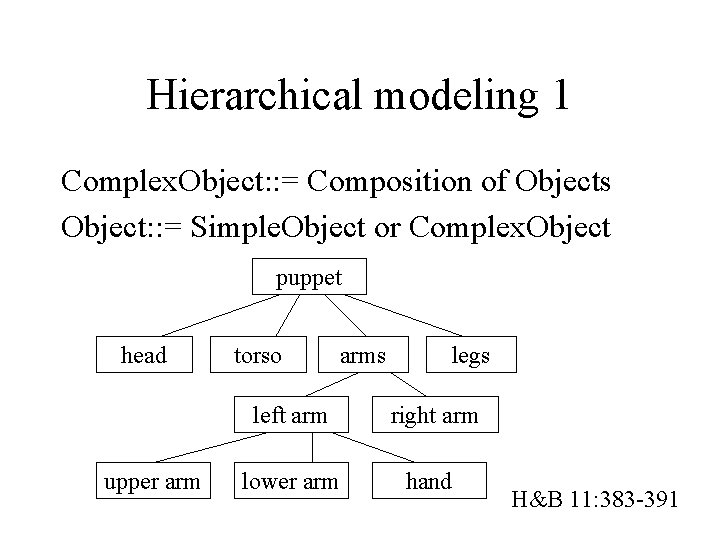
Hierarchical modeling 1 Complex. Object: : = Composition of Objects Object: : = Simple. Object or Complex. Object puppet head upper arm torso arms legs left arm right arm lower arm hand H&B 11: 383 -391

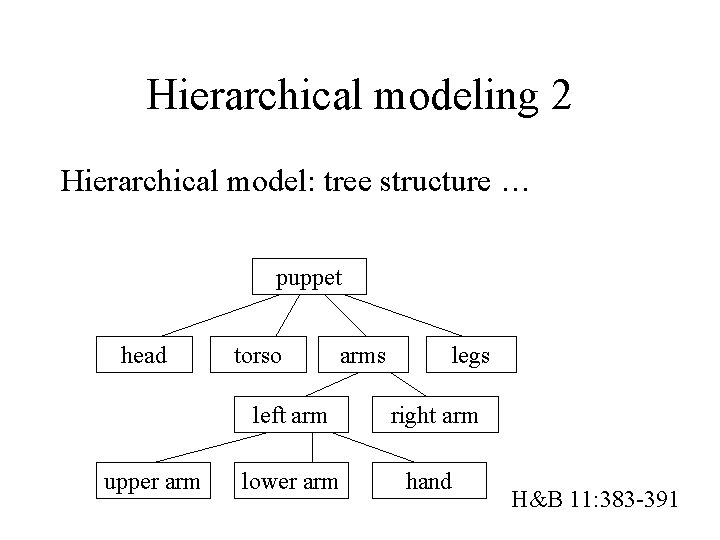
Hierarchical modeling 2 Hierarchical model: tree structure … puppet head upper arm torso arms legs left arm right arm lower arm hand H&B 11: 383 -391

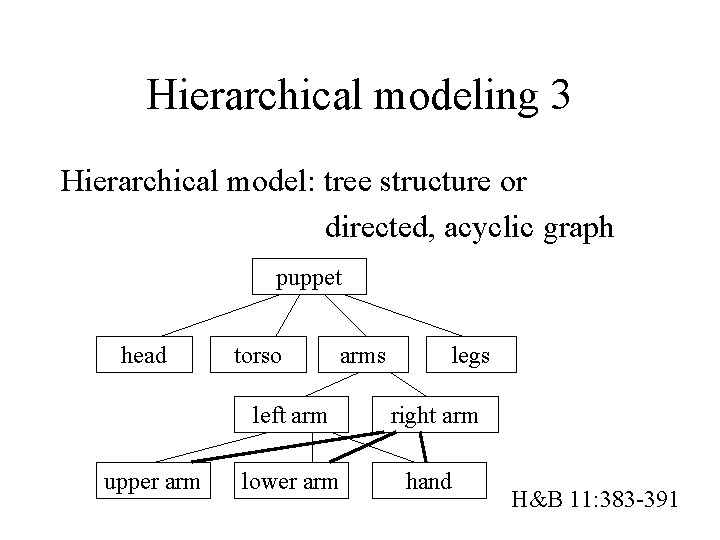
Hierarchical modeling 3 Hierarchical model: tree structure or directed, acyclic graph puppet head upper arm torso arms legs left arm right arm lower arm hand H&B 11: 383 -391

Hierarchical modeling 4 Scene graph: Leaf: primitive object geometric object, possibly parametrised Composite node: instruction for composition (usually union) Leafs, nodes and/or edges: transformations + other data Implementation: data (read model, generic engine) or code (translate into statements & calls). H&B 11: 383 -391

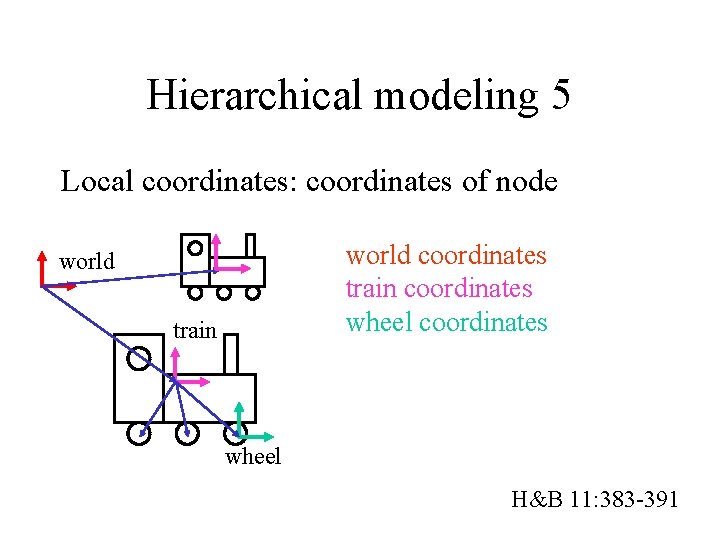
Hierarchical modeling 5 Local coordinates: coordinates of node world coordinates train coordinates wheel coordinates world train wheel H&B 11: 383 -391

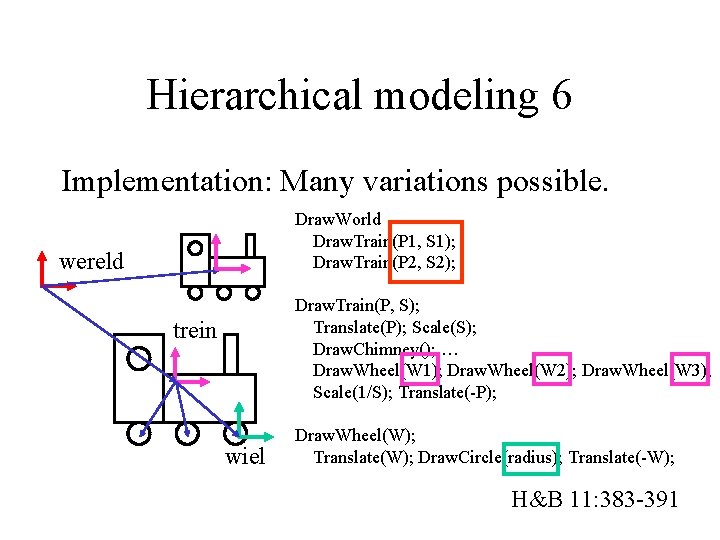
Hierarchical modeling 6 Implementation: Many variations possible. Draw. World Draw. Train(P 1, S 1); Draw. Train(P 2, S 2); wereld Draw. Train(P, S); Translate(P); Scale(S); Draw. Chimney(); … Draw. Wheel(W 1); Draw. Wheel(W 2); Draw. Wheel(W 3); Scale(1/S); Translate(-P); trein wiel Draw. Wheel(W); Translate(W); Draw. Circle(radius); Translate(-W); H&B 11: 383 -391

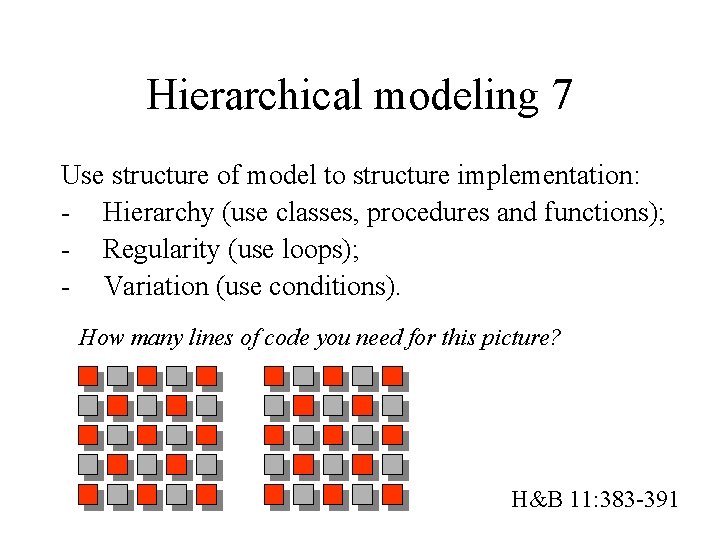
Hierarchical modeling 7 Use structure of model to structure implementation: - Hierarchy (use classes, procedures and functions); - Regularity (use loops); - Variation (use conditions). How many lines of code you need for this picture? H&B 11: 383 -391

Hierarchical modeling 7 Draw. Two. Grids Draw. Grid; Translate(7, 0); Draw. Grid; How many lines of code you need for this picture? Mwah, 10 -20 should do Aim for as clean as possible, not as compact as possible Draw. Grid for i : = 1 to 5 do for j : = 1 to 5 do Draw. Cell(i, j, (i+j) mod 2 = 0); Draw. Cell(x, y, use_red) Set. Color(dark_grey); Draw. Rect(x+0. 2, y, 0. 7); if use_red then Set. Color(red) else Set. Color(light_grey); Draw. Rect(x, y+0. 2, 0. 7); H&B 11: 383 -391

Next… • We know how to transform objects • Next step: Viewing objects