2 Graphs and Functions Copyright 2015 2011 2005

A Library of Parent Functions 2. 4 • Continuity • The Identity, Squaring, and

Continuity (Informal Definition) A function is continuous over an interval of its domain if

Example 1 DETERMINING INTERVALS OF CONTINUTIY Describe the intervals of continuity for each function.

IDENTITY FUNCTION (x) = x Domain: (– , ) x – 2 – 1

SQUARING FUNCTION (x) = x 2 Domain: (– , ) x – 2 –

CUBING FUNCTION (x) = x 3 Domain: (– , ) x – 2 –

SQUARE ROOT FUNCTION (x) = Domain: [0, ) x 0 1 4 9 16

CUBE ROOT FUNCTION (x) = Domain: (– , ) x – 8 – 1

ABSOLUTE VALUE FUNCTION (x) = Domain: (– , ) x – 2 – 1

Example 2 GRAPHING PIECEWISE-DEFINED FUNCTIONS Graph each function. (a) (b) Copyright © 2015, 2011,

Example 2 GRAPHING PIECEWISE-DEFINED FUNCTIONS Graph each function. y (a) Solution Graph each interval

Example 2 GRAPHING PIECEWISE-DEFINED FUNCTIONS Graph the function. (b) Solution The two graphs meet

Copyright © 2015, 2011, 2005 Pearson Education, Inc. 15 2. 6 - 15

GREATEST INTEGER FUNCTION (x) = Domain: (– , ) Range: {y y is an

GRAPHING A GREATEST INTEGER FUNCTION Example 3 Graph Solution If x is in the

Example 4 APPLYING A GREATEST INTEGER FUNCTION An express mail company charges $25 for

APPLYING A GREATEST INTEGER FUNCTION Example 4 y Solution For x in the interval

The Relation x = y 2 Recall that a function is a relation where

Slides: 20

Download presentation

A Library of Parent Functions 2. 4 • Continuity • The Identity, Squaring, and Cubing Functions • The Square Root and Cube Root Functions • The Absolute Function • Piecewise-Defined Functions • The Relation x = y 2 Copyright © 2015, 2011, 2005 Pearson Education, Inc. 2

Continuity (Informal Definition) A function is continuous over an interval of its domain if its hand-drawn graph over that interval can be sketched without lifting the pencil from the paper. Copyright © 2015, 2011, 2005 Pearson Education, Inc. 32. 6 - 3

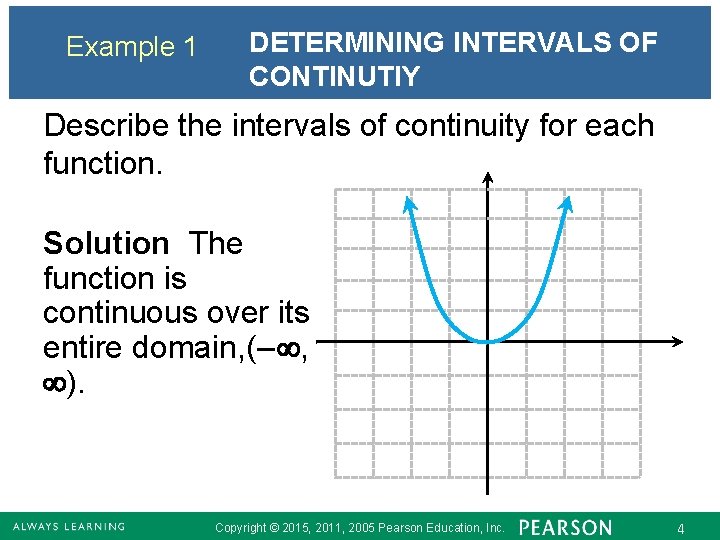
Example 1 DETERMINING INTERVALS OF CONTINUTIY Describe the intervals of continuity for each function. Solution The function is continuous over its entire domain, (– , ). Copyright © 2015, 2011, 2005 Pearson Education, Inc. 4

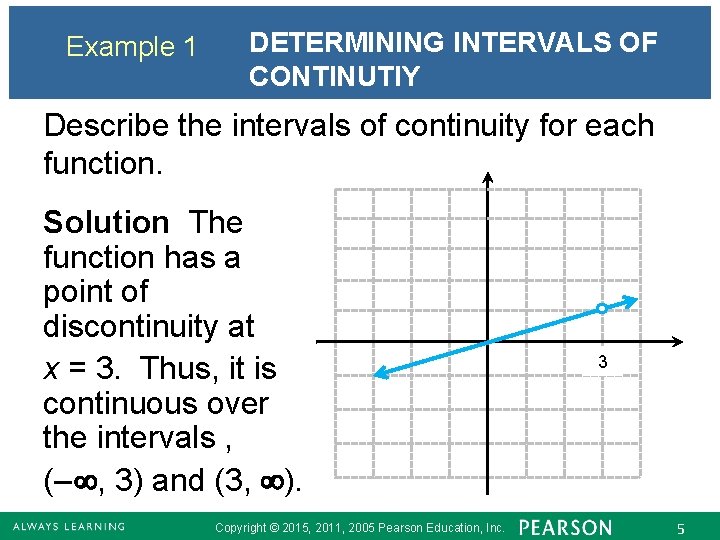
Example 1 DETERMINING INTERVALS OF CONTINUTIY Describe the intervals of continuity for each function. Solution The function has a point of discontinuity at x = 3. Thus, it is continuous over the intervals , (– , 3) and (3, ). Copyright © 2015, 2011, 2005 Pearson Education, Inc. 3 5

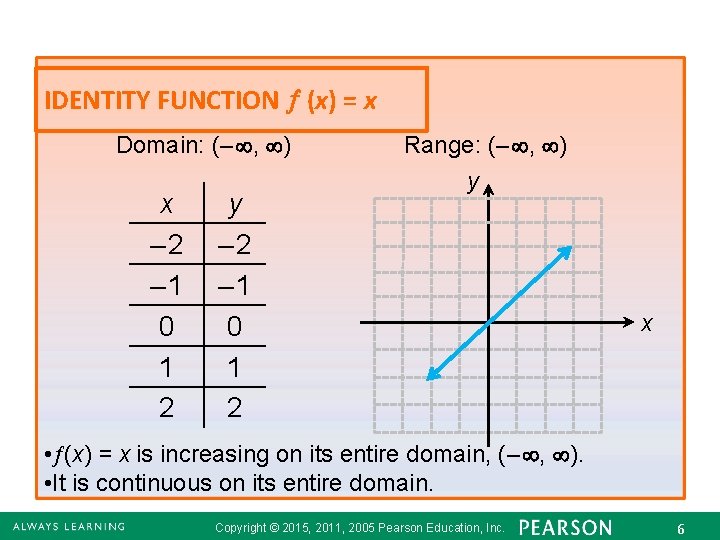
IDENTITY FUNCTION (x) = x Domain: (– , ) x – 2 – 1 0 1 2 y – 2 – 1 0 1 2 Range: (– , ) y x • (x) = x is increasing on its entire domain, (– , ). • It is continuous on its entire domain. Copyright © 2015, 2011, 2005 Pearson Education, Inc. 62. 6 - 6

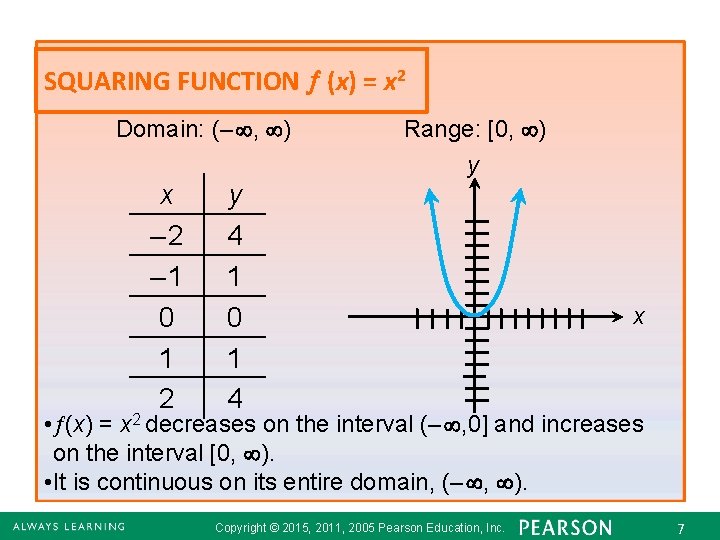
SQUARING FUNCTION (x) = x 2 Domain: (– , ) x – 2 – 1 0 1 2 Range: [0, ) y y 4 1 0 1 4 x • (x) = x 2 decreases on the interval (– , 0] and increases on the interval [0, ). • It is continuous on its entire domain, (– , ). Copyright © 2015, 2011, 2005 Pearson Education, Inc. 72. 6 - 7

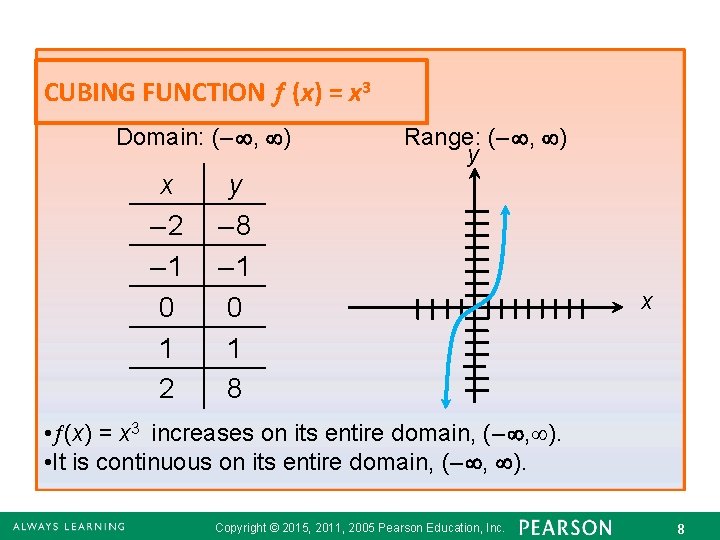
CUBING FUNCTION (x) = x 3 Domain: (– , ) x – 2 – 1 0 1 2 Range: (– , ) y y – 8 – 1 0 1 8 x • (x) = x 3 increases on its entire domain, (– , ). • It is continuous on its entire domain, (– , ). Copyright © 2015, 2011, 2005 Pearson Education, Inc. 82. 6 - 8

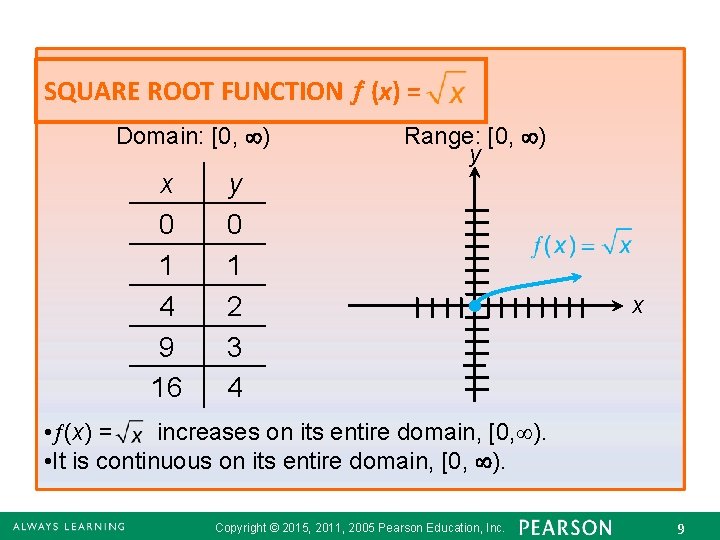
SQUARE ROOT FUNCTION (x) = Domain: [0, ) x 0 1 4 9 16 Range: [0, ) y y 0 1 2 3 4 x • (x) = increases on its entire domain, [0, ). • It is continuous on its entire domain, [0, ). Copyright © 2015, 2011, 2005 Pearson Education, Inc. 92. 6 - 9

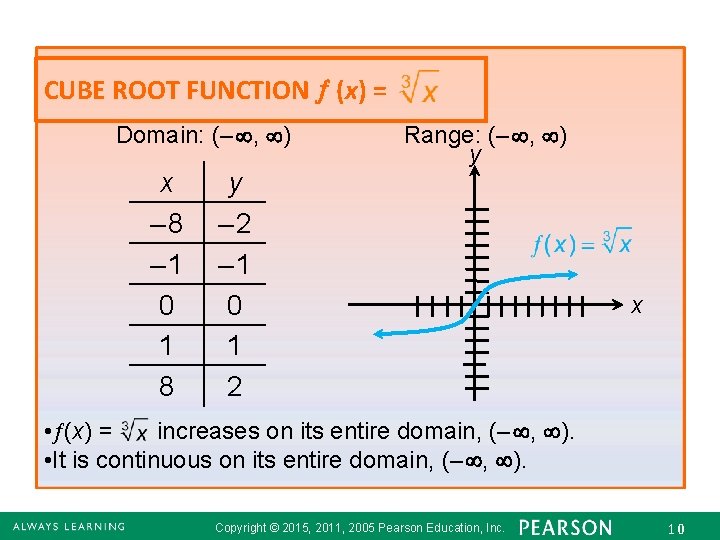
CUBE ROOT FUNCTION (x) = Domain: (– , ) x – 8 – 1 0 1 8 y – 2 – 1 0 1 2 Range: (– , ) y x • (x) = increases on its entire domain, (– , ). • It is continuous on its entire domain, (– , ). Copyright © 2015, 2011, 2005 Pearson Education, Inc. 10 2. 6 - 10

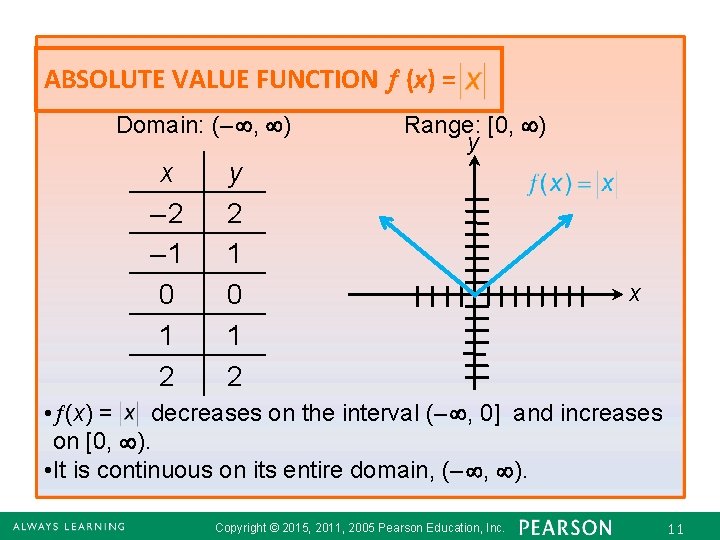
ABSOLUTE VALUE FUNCTION (x) = Domain: (– , ) x – 2 – 1 0 1 2 Range: [0, ) y y 2 1 0 1 2 x • (x) = decreases on the interval (– , 0] and increases on [0, ). • It is continuous on its entire domain, (– , ). Copyright © 2015, 2011, 2005 Pearson Education, Inc. 11 2. 6 - 11

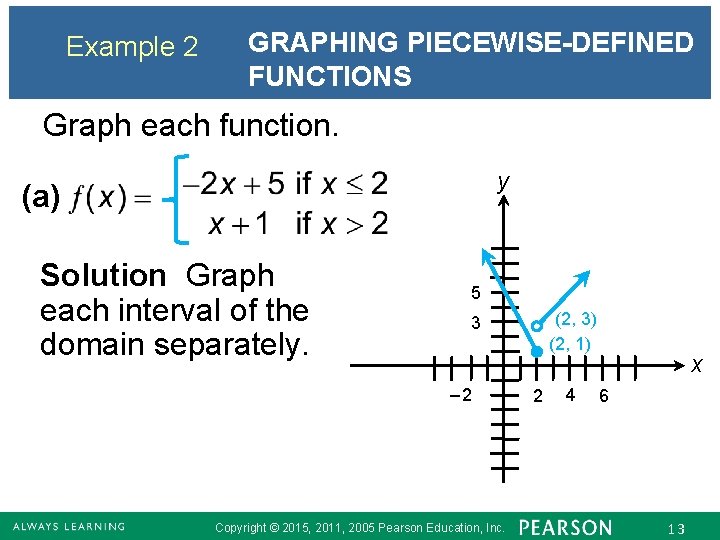
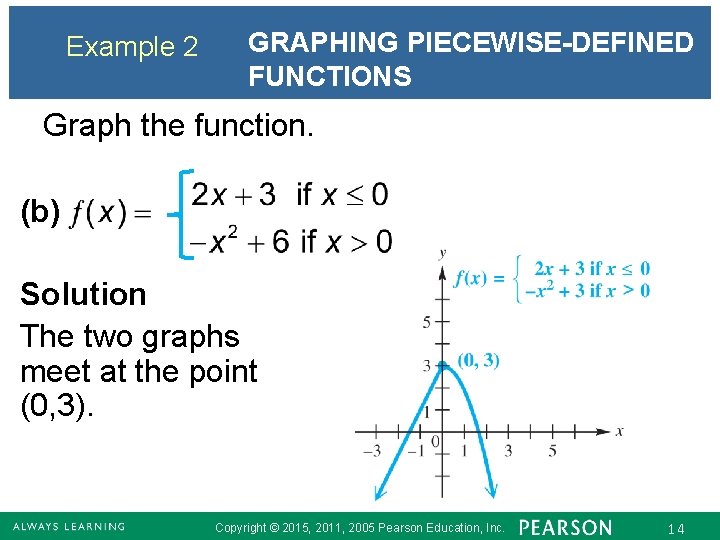
Example 2 GRAPHING PIECEWISE-DEFINED FUNCTIONS Graph each function. y (a) Solution Graph each interval of the domain separately. 5 (2, 3) (2, 1) 3 – 2 Copyright © 2015, 2011, 2005 Pearson Education, Inc. 2 4 x 6 13

GREATEST INTEGER FUNCTION (x) = Domain: (– , ) Range: {y y is an integer} = {…– 3, – 2, – 1, 0, 1, 2, 3, …} x – 2 – 1. 5 – 0. 99 y – 2 – 1 0 0. 001 3 3. 99 0 0 3 3 4 3 2 – 4– 3 – 2 1 1 2 3 4 – 2 – 3 – 4 • (x) = is constant on the intervals…, [– 2, – 1), [– 1, 0), [0, 1), [1, 2), [2, 3), …. • It is discontinuous at all integer values in its domain (– , ). Copyright © 2015, 2011, 2005 Pearson Education, Inc. 16

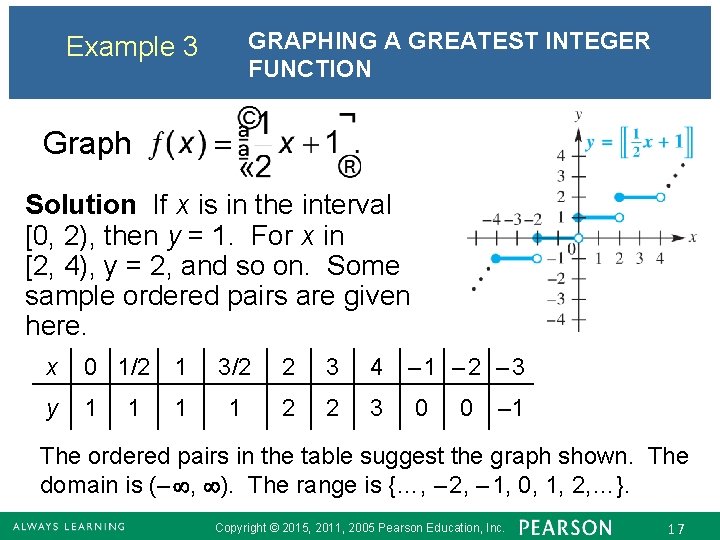
GRAPHING A GREATEST INTEGER FUNCTION Example 3 Graph Solution If x is in the interval [0, 2), then y = 1. For x in [2, 4), y = 2, and so on. Some sample ordered pairs are given here. x 0 1/2 1 y 1 1 1 3/2 2 3 4 1 2 2 3 – 1 – 2 – 3 0 0 – 1 The ordered pairs in the table suggest the graph shown. The domain is (– , ). The range is {…, – 2, – 1, 0, 1, 2, …}. Copyright © 2015, 2011, 2005 Pearson Education, Inc. 17

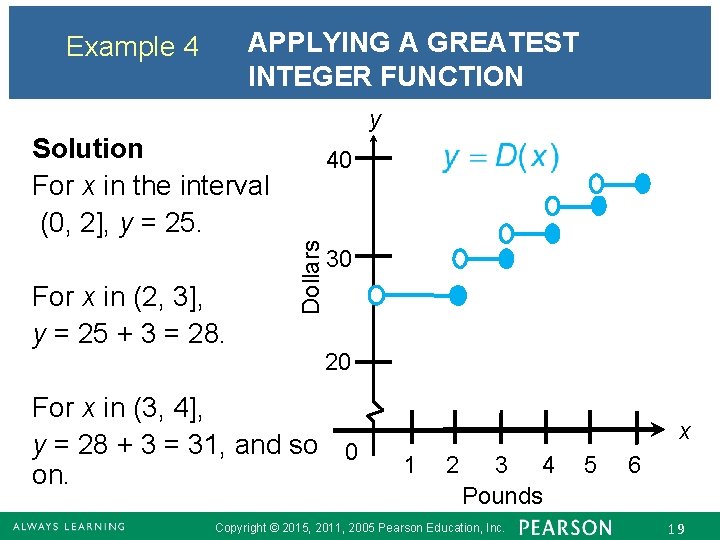
Example 4 APPLYING A GREATEST INTEGER FUNCTION An express mail company charges $25 for a package weighing up to 2 lb. For each additional pound or fraction of a pound there is an additional charge of $3. Let y = D(x) represent the cost to send a package weighing x pounds. Graph y = D(x) for x in the interval (0, 6]. Copyright © 2015, 2011, 2005 Pearson Education, Inc. 18

APPLYING A GREATEST INTEGER FUNCTION Example 4 y Solution For x in the interval (0, 2], y = 25. Dollars For x in (2, 3], y = 25 + 3 = 28. 40 30 20 For x in (3, 4], y = 28 + 3 = 31, and so 0 on. x 1 2 3 4 Pounds Copyright © 2015, 2011, 2005 Pearson Education, Inc. 5 6 19

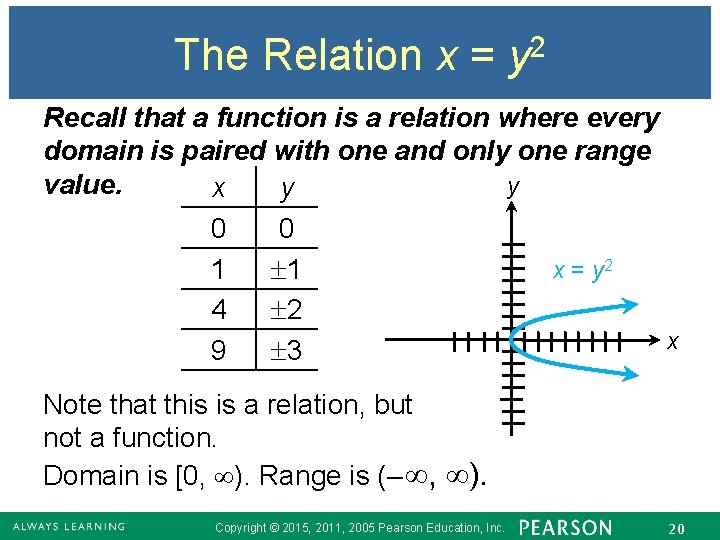
The Relation x = y 2 Recall that a function is a relation where every domain is paired with one and only one range value. y x y 0 0 x = y 2 1 1 4 2 x 9 3 Note that this is a relation, but not a function. Domain is [0, ). Range is (– , ). Copyright © 2015, 2011, 2005 Pearson Education, Inc. 20