2 Elements of Ensemble Theory 1 Phase Space

2. Elements of Ensemble Theory 1. Phase Space of a Classical System 2. Liouville’s Theorem & Its Consequences 3. The Microcanonical Ensemble 4. Examples 5. Quantum States & the Phase Space

At equilibrium: Each macrostate represents a huge number of microstates. Observed values ~ time averaged over microstates. Ensemble theory: Ensemble average = Time average

2. 1. Phase Space of a Classical System Hamiltonian formulism of mechanics: Each dynamical state of a system of N particles is specified by 3 N position coordinates { qi }, and 3 N momentum coordinates { pi }, i. e. , by a point { qi , pi } in the 6 N –D phase space of the system. Time evolution of the system is described by a path in phase space satisfying For a conservative system, its phase space trajectory is restricted to the hypersurface For a system in thermal equilibrium with a heat reservoir, its phase space trajectory is restricted to the “hypershell”

Ensemble of a system: Set of identical copies of a system that includes every distinct state that satisfies the given boundary conditions and gives rise to the given macrostate. In thermodynamical limit ( N, V , N / V = finite ) , the phase points of the ensemble form a continuum. The ensemble average of a dynamical function f is given by = density function An ensemble is stationary if f is t – indep. Ensemble of a system in equilibrium must be stationary.

2. 2. Liouville’s Theorem & Its Consequences Liouville’s theorem where the Poisson bracket is defined as : # of phase points are conserved The current density of phase points is a 6 N-D vector

where Hence, the Liouville eq. is just the equation of continuity of the phase points : For a system in equilibrium

Solution 1: region of acceptible microstates in phase space. Microcanonical ensemble Principle of equal a priori probability : Solution 2: Chap 3: Canonical ensemble

2. 3. The Microcanonical Ensemble 1. Hypersurface 2. Hypershell f ensemble average of f = time average of f for systems in eqm. = time average of f 2 av are indep = long time average of f over 1 ensemble member = f measured Let 0 fundamental volume of one microstate. Then

2. 4. Examples Microcanonical Classical ideal gas: Surface area of an n-D sphere (App. C) is

Sec 1. 4 : Volume of state per degree of freedom = h

Single Free Particle Confined to V

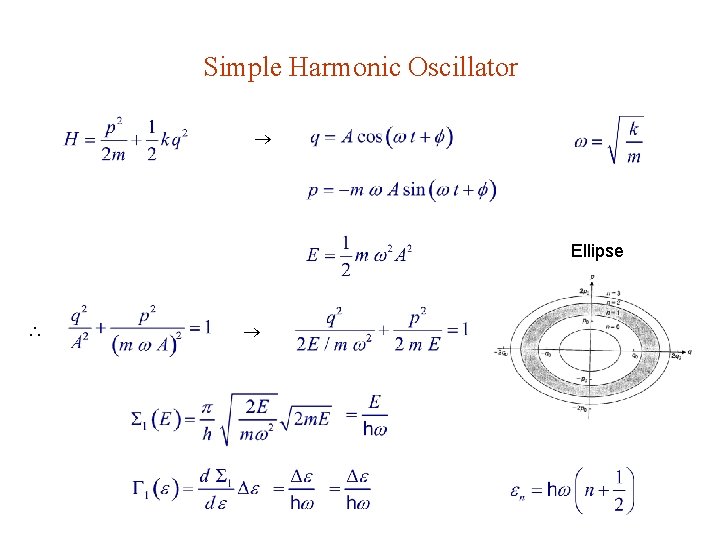
Simple Harmonic Oscillator Ellipse

2. 5. Quantum States & the Phase Space Phase space volume of 1 quantum state may be estimated from the uncertainty principle: Among the first to suggest Bose (black-body radiation) : Cf. Rayleigh’s number of modes are Tetrode, Sackur, & Bose. for photons Caution: Above formulae consider only a single polarization component.