2 Eddy Current Theory 2 1 Eddy Current

2 Eddy Current Theory 2. 1 Eddy Current Method 2. 2 Impedance Measurements 2. 3 Impedance Diagrams 2. 4 Test Coil Impedance 2. 5 Field Distributions

2. 1 Eddy Current Method

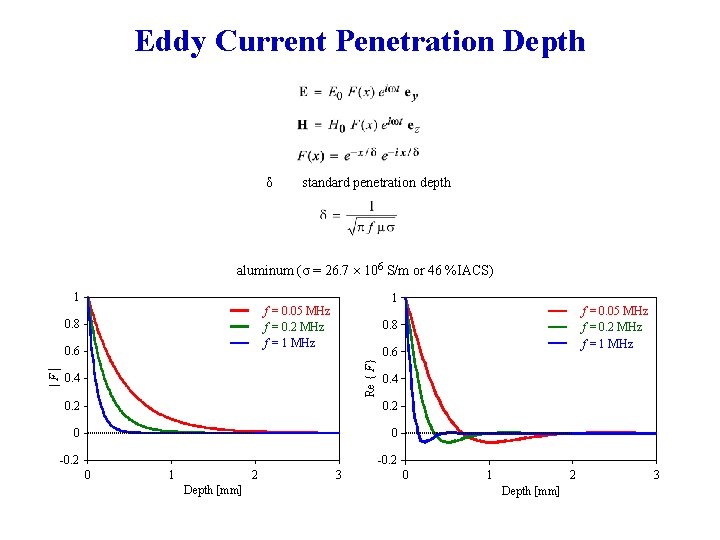
Eddy Current Penetration Depth δ standard penetration depth aluminum (σ = 26. 7 106 S/m or 46 %IACS) 1 0. 8 f = 0. 05 MHz f = 0. 2 MHz f = 1 MHz 0. 8 0. 6 Re { F} 0. 6 |F| 1 f = 0. 05 MHz f = 0. 2 MHz f = 1 MHz 0. 4 0. 2 0 0 -0. 2 0 1 2 Depth [mm] 3

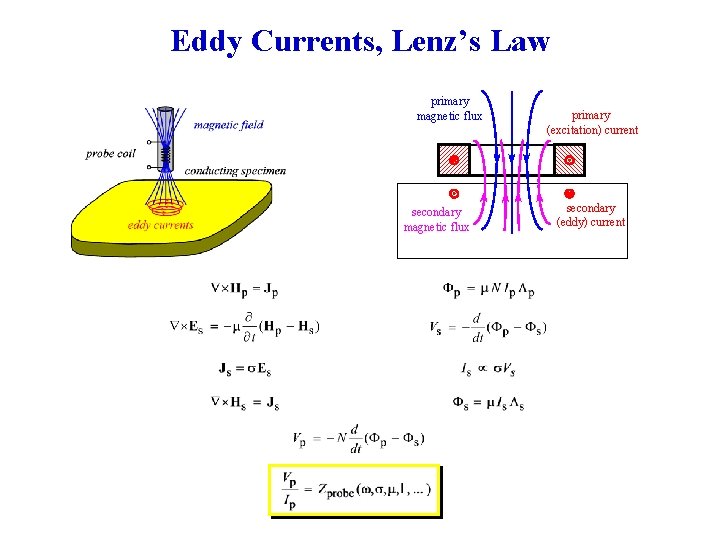
Eddy Currents, Lenz’s Law primary magnetic flux secondary magnetic flux primary (excitation) current secondary (eddy) current

2. 2 Impedance Measurements

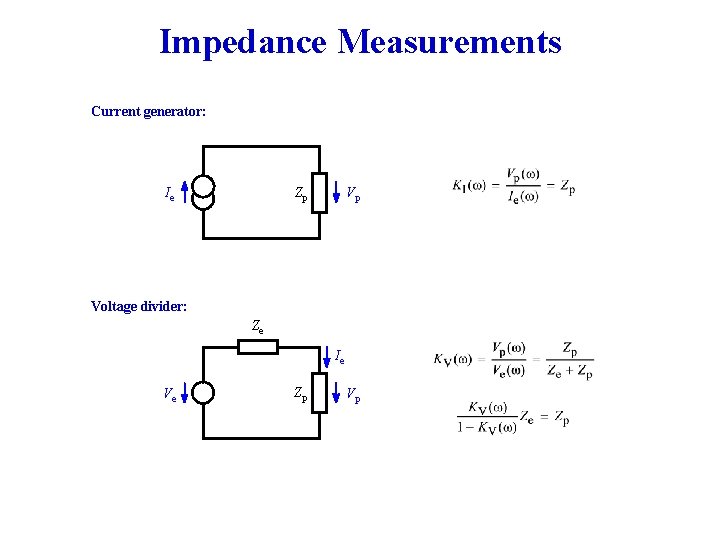
Impedance Measurements Current generator: Zp Ie Vp Voltage divider: Ze Ie Ve Zp Vp

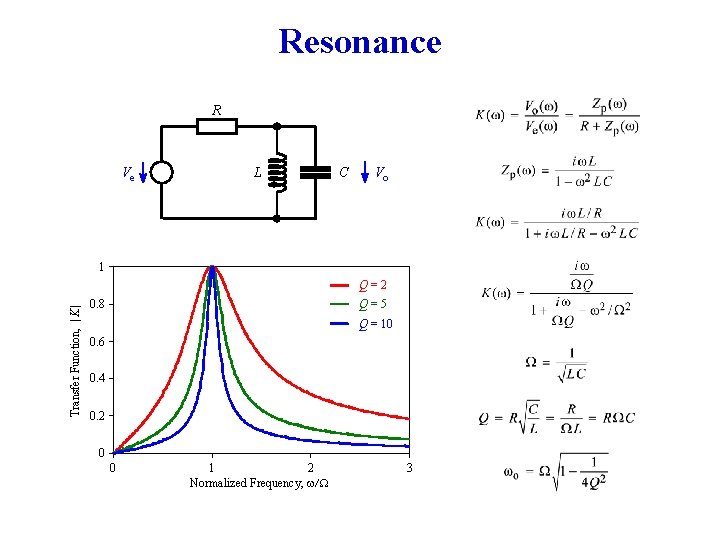
Resonance R Ve L C Vo 1 Transfer Function, | K | Q=2 0. 8 Q=5 Q = 10 0. 6 0. 4 0. 2 0 0 1 2 Normalized Frequency, w/W 3

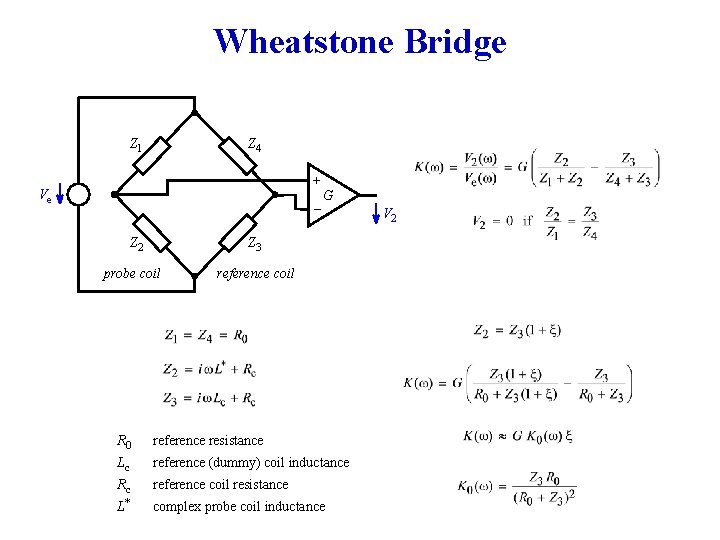
Wheatstone Bridge Z 1 Z 4 + Ve _G Z 2 Z 3 probe coil reference coil R 0 reference resistance Lc reference (dummy) coil inductance Rc reference coil resistance L* complex probe coil inductance V 2

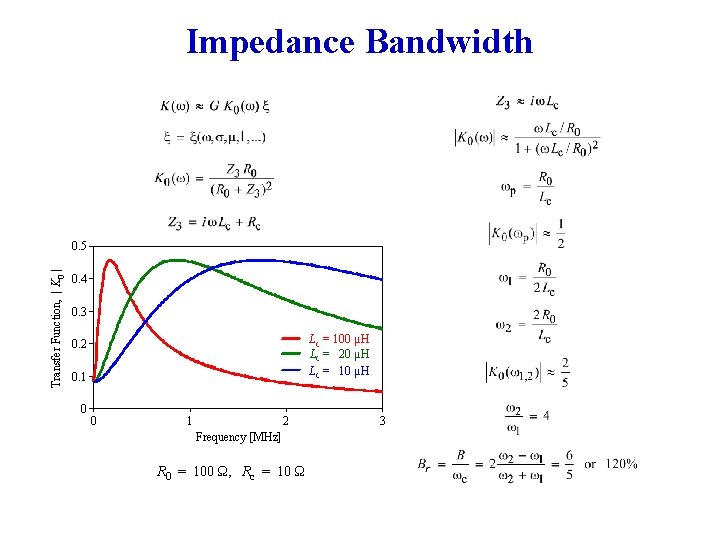
Impedance Bandwidth Transfer Function, | K 0 | 0. 5 0. 4 0. 3 Lc = 100 µH Lc = 20 µH Lc = 10 µH 0. 2 0. 1 0 0 1 2 Frequency [MHz] R 0 = 100 Ω, Rc = 10 Ω 3

2. 3 Impedance Diagrams

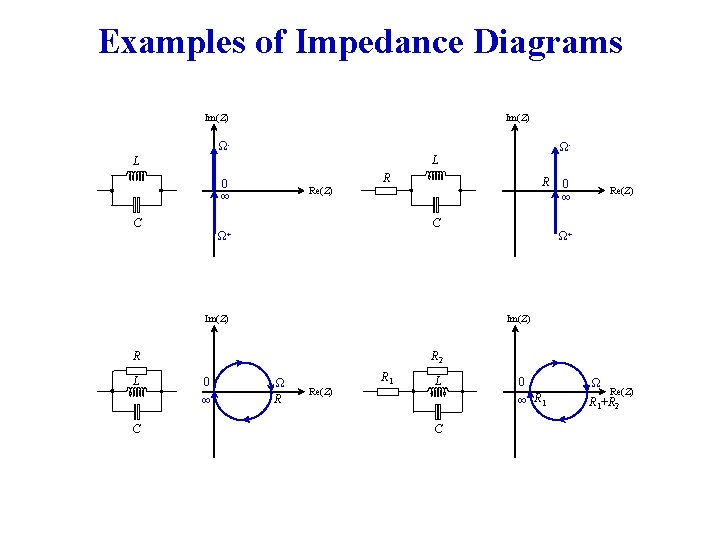
Examples of Impedance Diagrams Im(Z) Ω- ΩL L R 0 ∞ R Re(Z) Ω+ Ω+ Im(Z) R 2 R 0 ∞ C Re(Z) C C L 0 ∞ Ω R R 1 Re(Z) L C 0 Ω ∞ R 1+R 2 Re(Z)

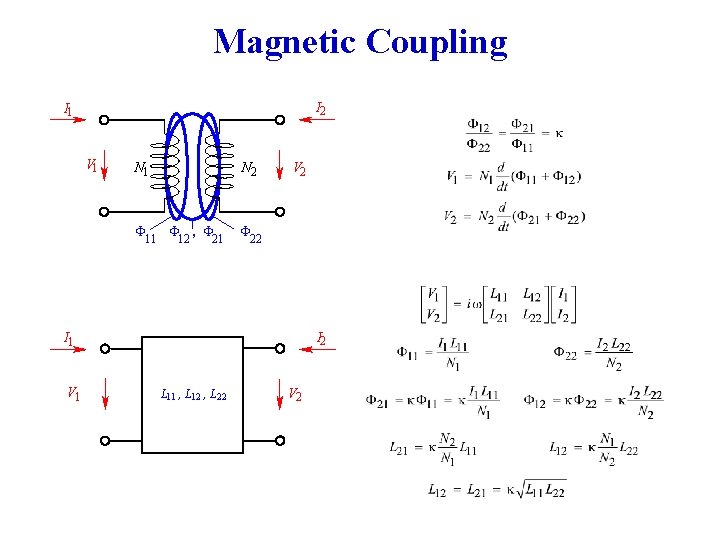
Magnetic Coupling I 2 I 1 V 1 N 2 F 11 F 12 , F 21 F 22 V 2 I 1 V 1 L 11 , L 12 , L 22 V 2

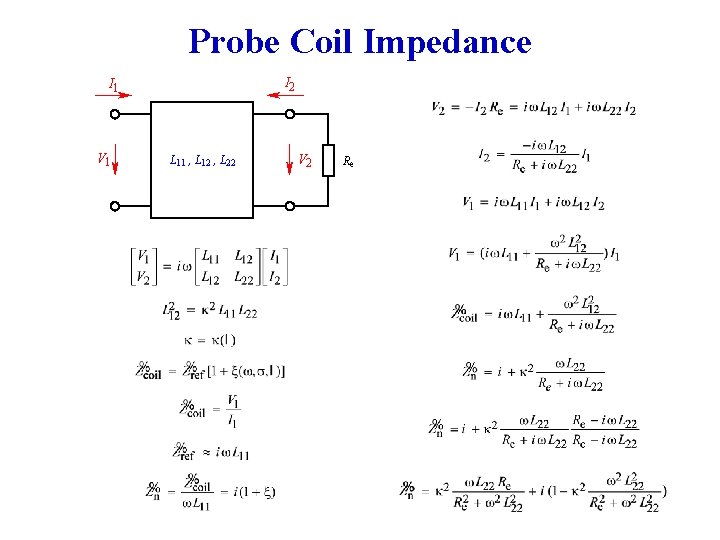
Probe Coil Impedance I 2 I 1 V 1 L 11 , L 12 , L 22 V 2 Re

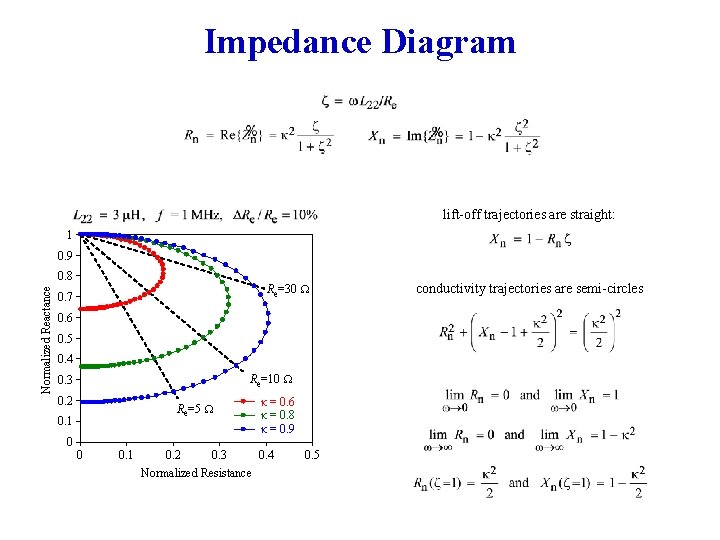
Impedance Diagram lift-off trajectories are straight: 1 0. 9 Normalized Reactance 0. 8 Re=30 W 0. 7 0. 6 0. 5 0. 4 Re=10 W 0. 3 0. 2 Re=5 W 0. 1 0 0 0. 1 κ = 0. 6 κ = 0. 8 κ = 0. 9 0. 2 0. 3 0. 4 Normalized Resistance 0. 5 conductivity trajectories are semi-circles

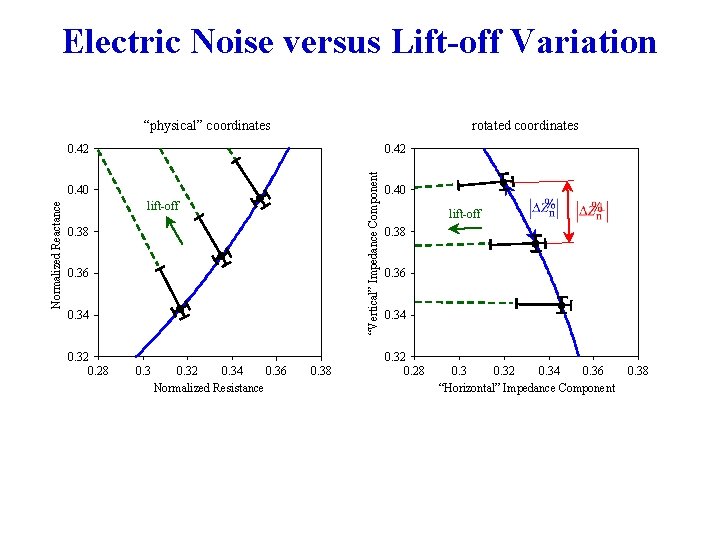
Electric Noise versus Lift-off Variation “physical” coordinates rotated coordinates 0. 42 “Vertical” Impedance Component 0. 42 Normalized Reactance 0. 40 lift-off 0. 38 0. 36 0. 34 0. 32 0. 28 0. 32 0. 34 0. 36 Normalized Resistance 0. 38 0. 40 lift-off 0. 38 0. 36 0. 34 0. 32 0. 28 0. 32 0. 34 0. 36 “Horizontal” Impedance Component 0. 38

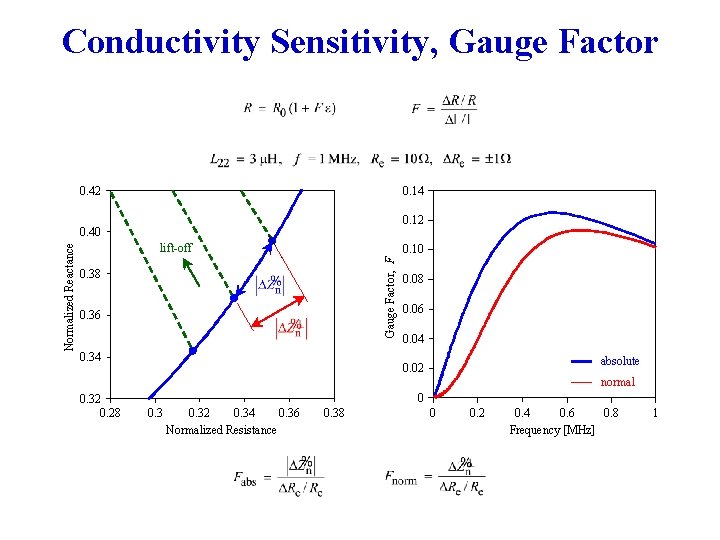
Conductivity Sensitivity, Gauge Factor 0. 14 0. 42 0. 12 lift-off 0. 10 Gauge Factor, F Normalized Reactance 0. 40 0. 38 0. 36 0. 34 0. 08 0. 06 0. 04 absolute 0. 02 normal 0. 32 0. 28 0 0. 32 0. 34 0. 36 Normalized Resistance 0. 38 0 0. 2 0. 4 0. 6 0. 8 Frequency [MHz] 1

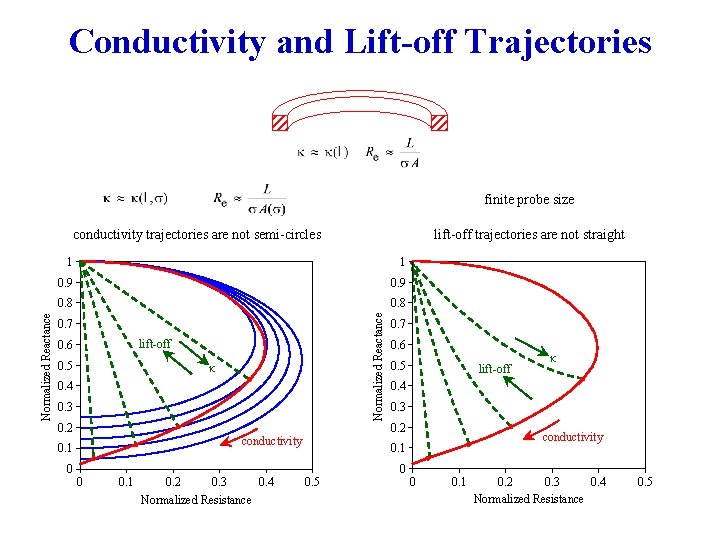
Conductivity and Lift-off Trajectories finite probe size lift-off trajectories are not straight 1 1 0. 9 0. 8 Normalized Reactance conductivity trajectories are not semi-circles 0. 7 lift-off 0. 6 0. 5 κ 0. 4 0. 3 0. 2 0 0 0. 1 0. 2 0. 3 0. 4 Normalized Resistance 0. 6 0. 5 lift-off 0. 3 conductivity 0. 1 0. 5 κ 0. 4 0. 2 conductivity 0. 1 0. 7 0 0 0. 1 0. 2 0. 3 0. 4 Normalized Resistance 0. 5

2. 4 Test Coil Impedance

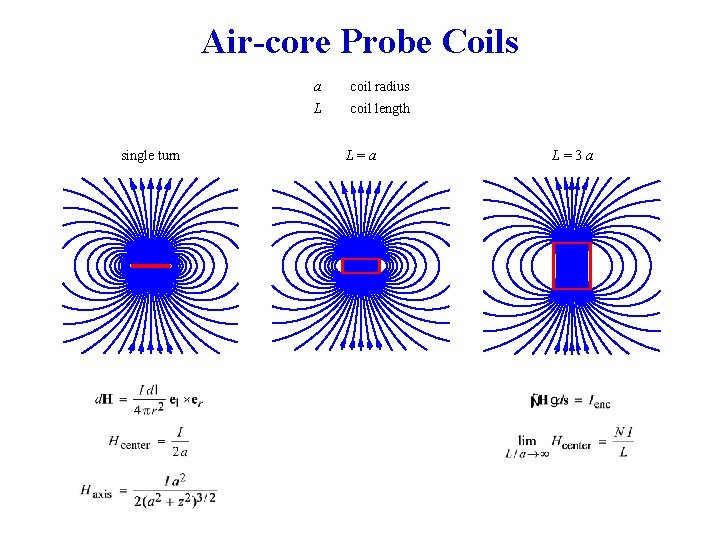
Air-core Probe Coils single turn a coil radius L coil length L=a L=3 a

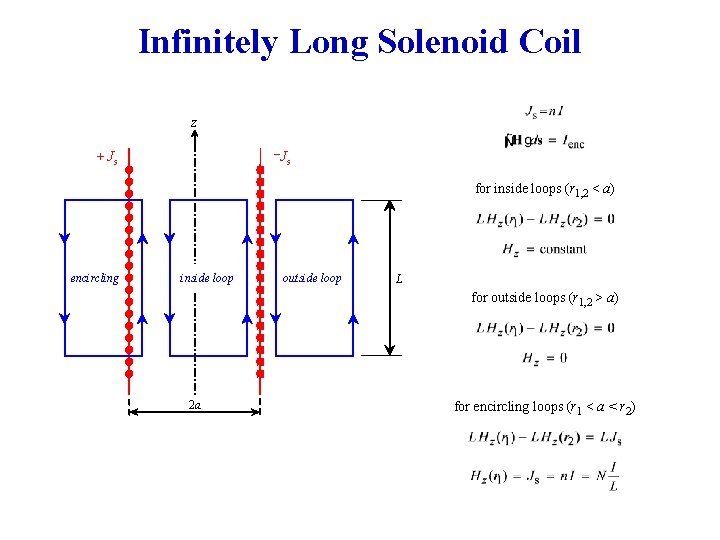
Infinitely Long Solenoid Coil z _ + Js Js for inside loops (r 1, 2 < a) encircling inside loop outside loop L for outside loops (r 1, 2 > a) 2 a for encircling loops (r 1 < a < r 2)

Magnetic Field of an Infinite Solenoid with Conducting Core z _ + Js Js in the air gap (b < r < a) Hz = J s in the core (0 < r < b) Hz = H 1 J 0(k r) Jn 2 b 2 a nth-order Bessel function of the first kind

Magnetic Flux of an Infinite Solenoid with Conducting Core z _ + Js 2 b 2 a Js

Impedance of an Infinite Solenoid with Conducting Core For an empty solenoid (b = 0): Normalized impedance:

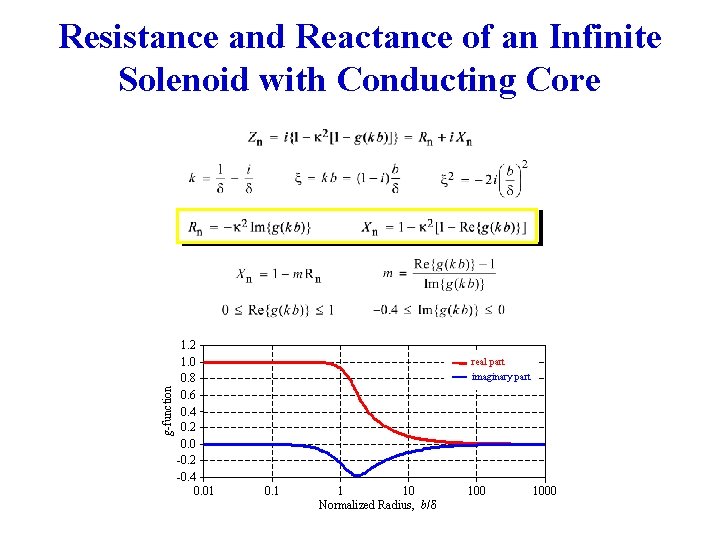
g-function Resistance and Reactance of an Infinite Solenoid with Conducting Core 1. 2 1. 0 0. 8 0. 6 0. 4 0. 2 0. 0 -0. 2 -0. 4 0. 01 real part imaginary part 0. 1 1 10 Normalized Radius, b/δ 1000

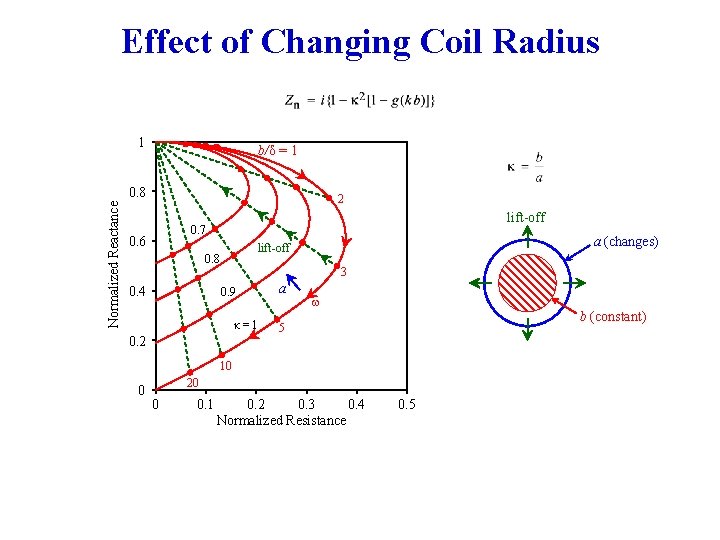
Effect of Changing Coil Radius 1 b/δ = 1 Normalized Reactance 0. 8 2 lift-off 0. 7 0. 6 a (changes) lift-off 0. 8 3 0. 4 0. 9 κ=1 0. 2 a w b (constant) 5 10 0 20 0 0. 1 0. 2 0. 3 0. 4 Normalized Resistance 0. 5

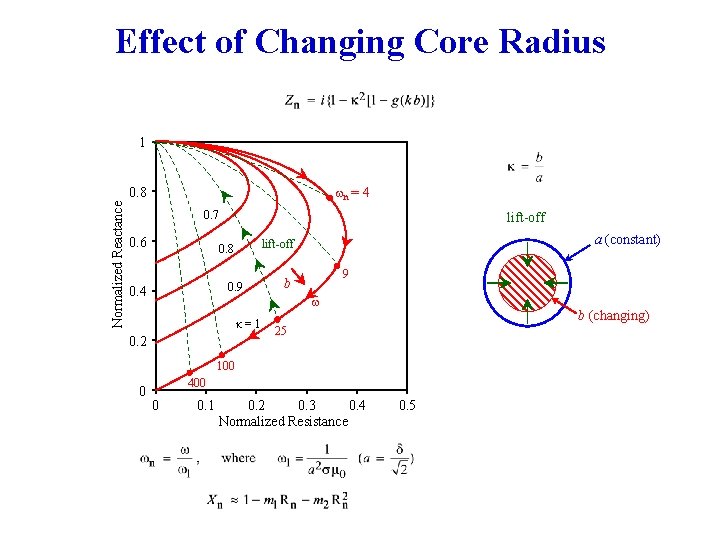
Effect of Changing Core Radius 1 Normalized Reactance 0. 8 wn = 4 0. 7 0. 6 lift-off 0. 9 0. 4 a (constant) lift-off 0. 8 9 b w κ=1 0. 2 b (changing) 25 100 0 400 0 0. 1 0. 2 0. 3 0. 4 Normalized Resistance 0. 5

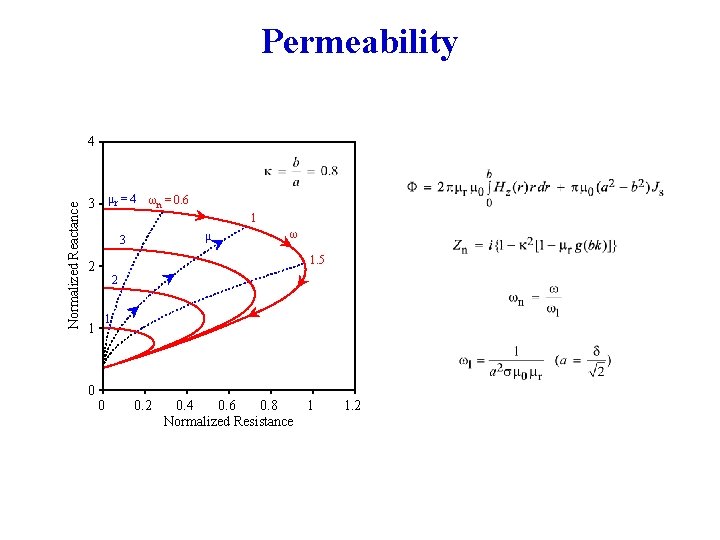
Permeability Normalized Reactance 4 3 µr = 4 ωn = 0. 6 1 µ 3 1. 5 2 1 0 ω 2 1 0 0. 2 0. 4 0. 6 0. 8 1 Normalized Resistance 1. 2

Solid Rod versus Tube solid rod BC 1: continuity of Hz at r = b a b tube BC 1: continuity of Hz at r = b BC 2: continuity of Hz at r = c BC 3: continuity of Eφ at r = c a c b

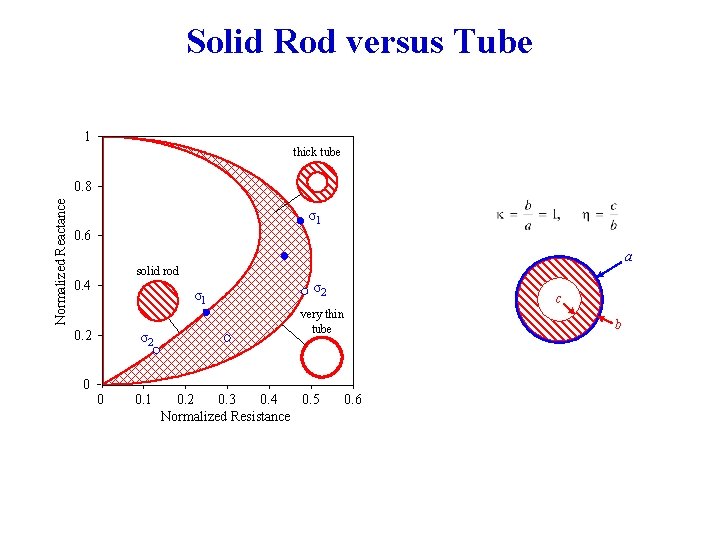
Solid Rod versus Tube 1 thick tube Normalized Reactance 0. 8 σ1 0. 6 a solid rod 0. 4 σ1 0. 2 0 σ2 0 0. 1 σ2 c very thin tube 0. 2 0. 3 0. 4 0. 5 Normalized Resistance b 0. 6

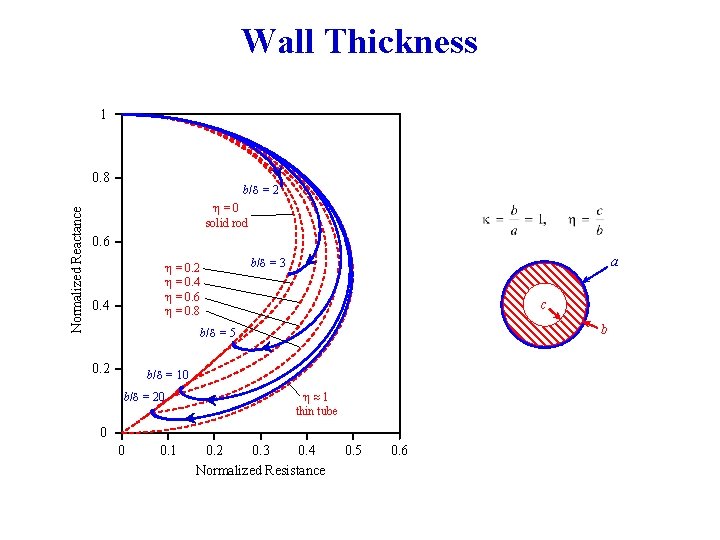
Wall Thickness 1 Normalized Reactance 0. 8 b/ = 2 η=0 solid rod 0. 6 η = 0. 2 η = 0. 4 η = 0. 6 η = 0. 8 0. 4 a b/ = 3 c b b/ = 5 0. 2 b/ = 10 b/ = 20 η 1 thin tube 0 0 0. 1 0. 2 0. 3 0. 4 Normalized Resistance 0. 5 0. 6

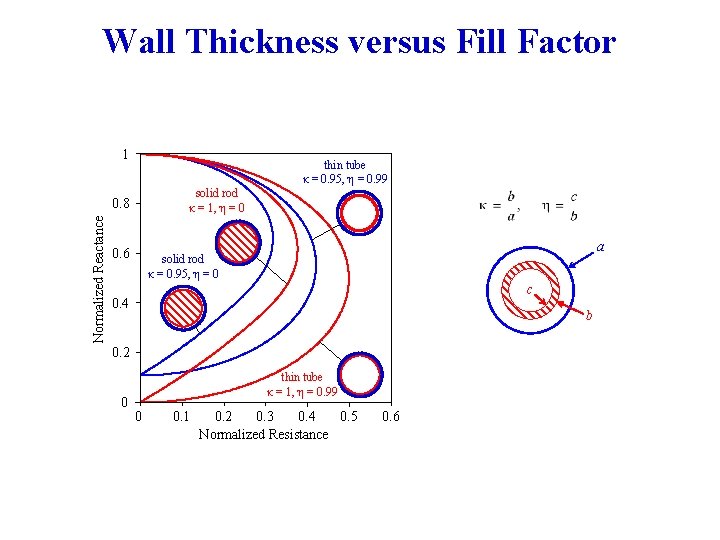
Wall Thickness versus Fill Factor 1 thin tube κ = 0. 95, η = 0. 99 solid rod κ = 1, η = 0 Normalized Reactance 0. 8 0. 6 a solid rod κ = 0. 95, η = 0 c 0. 4 b 0. 2 0 thin tube κ = 1, η = 0. 99 0 0. 1 0. 2 0. 3 0. 4 0. 5 Normalized Resistance 0. 6

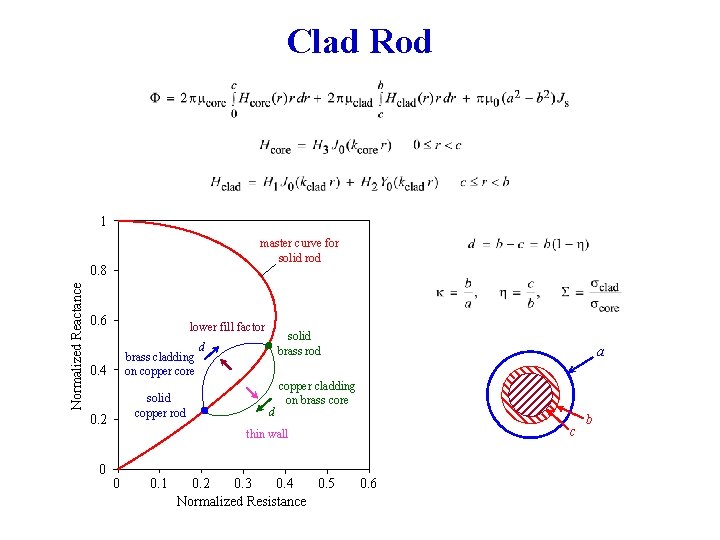
Clad Rod 1 master curve for solid rod Normalized Reactance 0. 8 0. 6 lower fill factor brass cladding on copper core 0. 4 solid copper rod 0. 2 0 solid brass rod d d a copper cladding on brass core c thin wall 0 0. 1 0. 2 0. 3 0. 4 0. 5 Normalized Resistance 0. 6 b

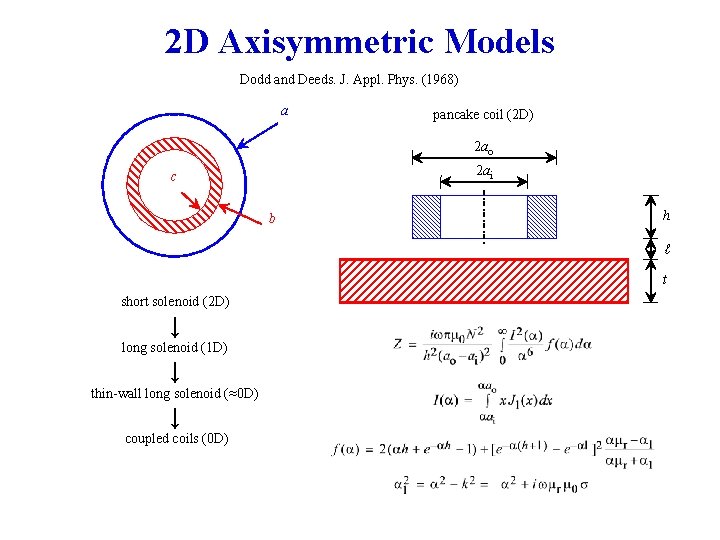
2 D Axisymmetric Models Dodd and Deeds. J. Appl. Phys. (1968) a pancake coil (2 D) 2 ao 2 ai c b h ℓ t short solenoid (2 D) ↓ long solenoid (1 D) ↓ thin-wall long solenoid (≈0 D) ↓ coupled coils (0 D)

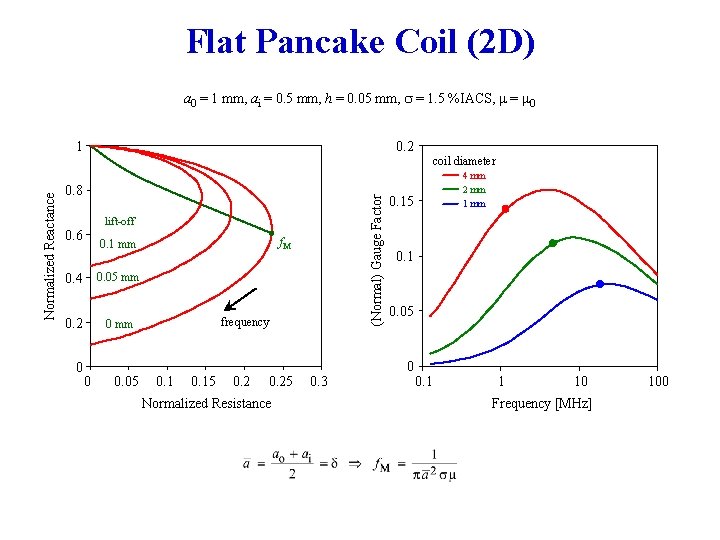
Flat Pancake Coil (2 D) a 0 = 1 mm, ai = 0. 5 mm, h = 0. 05 mm, = 1. 5 %IACS, = 0 0. 2 coil diameter 0. 8 lift-off 0. 6 f. M 0. 1 mm 0. 4 0. 05 mm 0. 2 0 mm 0 (Normal) Gauge Factor Normalized Reactance 1 0 0. 05 frequency 0. 15 0. 25 Normalized Resistance 0. 3 4 mm 2 mm 1 mm 0. 15 0. 1 0. 05 0 0. 1 1 10 Frequency [MHz] 100

2. 5 Field Distributions

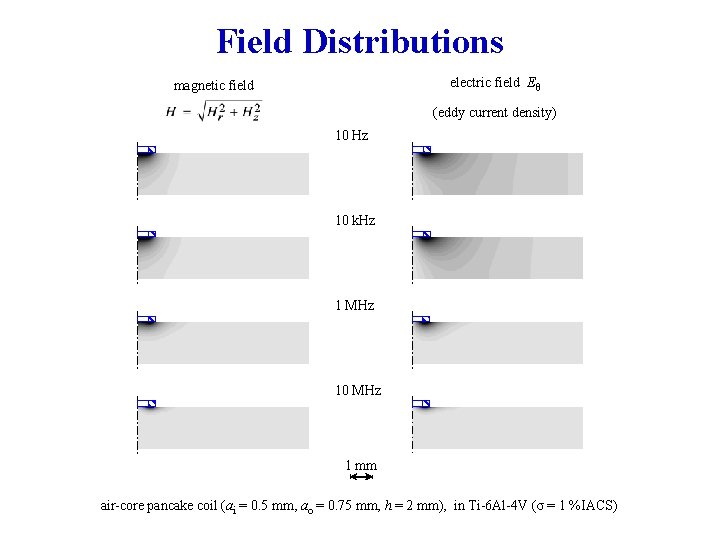
Field Distributions electric field Eθ magnetic field (eddy current density) 10 Hz 10 k. Hz 1 MHz 10 MHz 1 mm air-core pancake coil (ai = 0. 5 mm, ao = 0. 75 mm, h = 2 mm), in Ti-6 Al-4 V (σ = 1 %IACS)

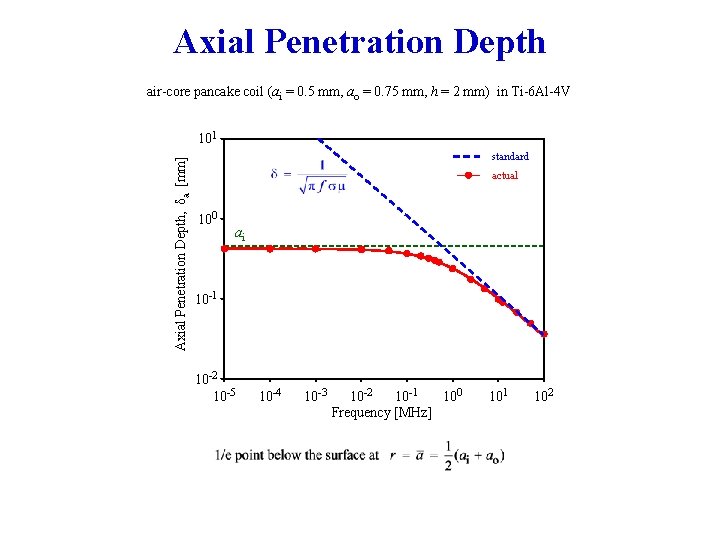
Axial Penetration Depth air-core pancake coil (ai = 0. 5 mm, ao = 0. 75 mm, h = 2 mm) in Ti-6 Al-4 V Axial Penetration Depth, δa [mm] 101 standard actual 100 ai 10 -1 10 -2 10 -5 10 -4 10 -3 10 -2 10 -1 100 Frequency [MHz] 101 102

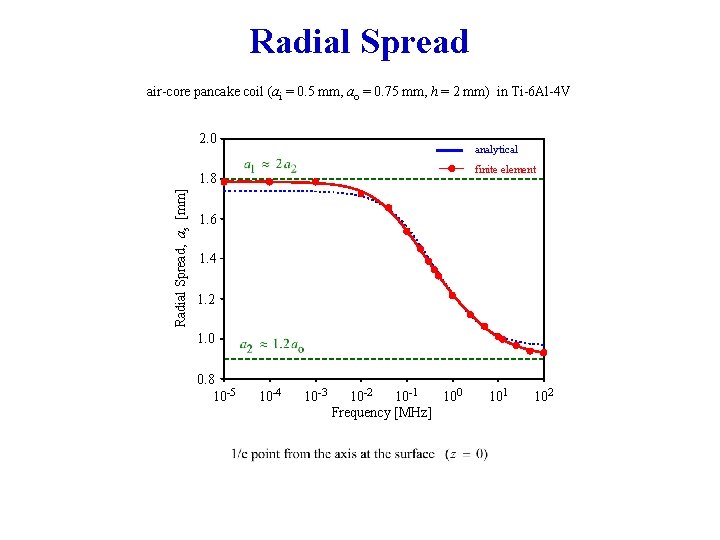
Radial Spread air-core pancake coil (ai = 0. 5 mm, ao = 0. 75 mm, h = 2 mm) in Ti-6 Al-4 V 2. 0 analytical finite element Radial Spread, as [mm] 1. 8 1. 6 1. 4 1. 2 1. 0 0. 8 10 -5 10 -4 10 -3 10 -2 10 -1 100 Frequency [MHz] 101 102

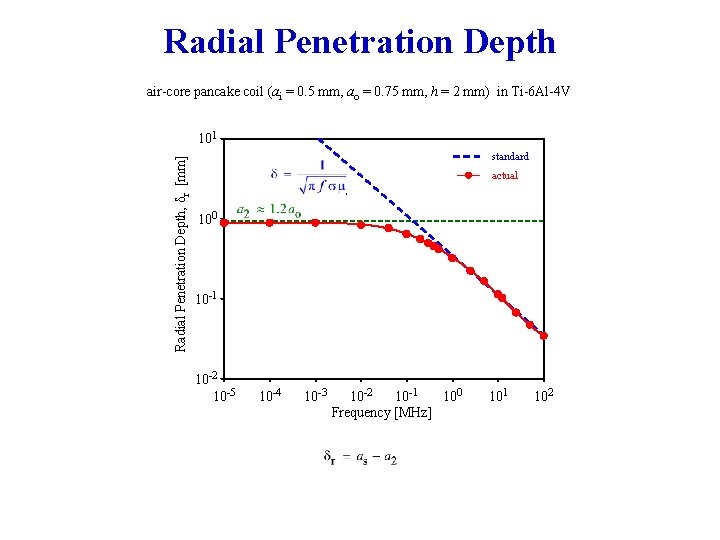
Radial Penetration Depth air-core pancake coil (ai = 0. 5 mm, ao = 0. 75 mm, h = 2 mm) in Ti-6 Al-4 V Radial Penetration Depth, δr [mm] 101 standard actual 100 10 -1 10 -2 10 -5 10 -4 10 -3 10 -2 10 -1 100 Frequency [MHz] 101 102

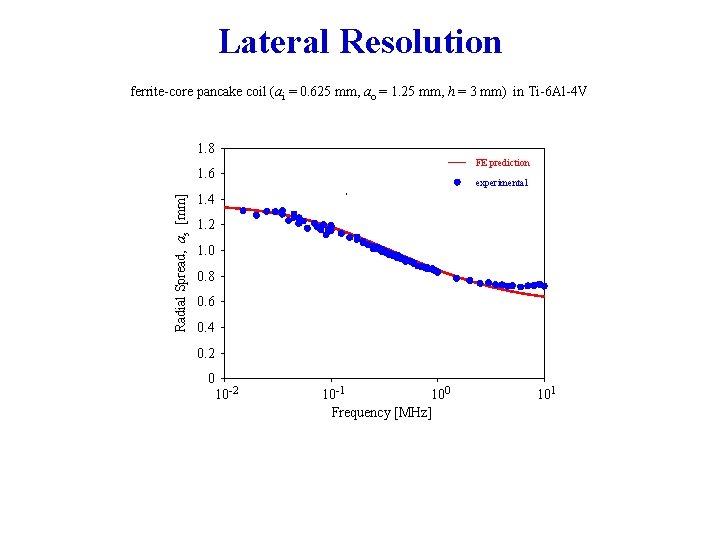
Lateral Resolution ferrite-core pancake coil (ai = 0. 625 mm, ao = 1. 25 mm, h = 3 mm) in Ti-6 Al-4 V 1. 8 FE prediction Radial Spread, as [mm] 1. 6 experimental 1. 4 1. 2 1. 0 0. 8 0. 6 0. 4 0. 2 0 10 -2 10 -1 100 Frequency [MHz] 101