2 Deformao Outra das repostas do slido ao

2. Deformação Outra das repostas do sólido ao carregamento O MC depois da aplicação da carga muda a sua posição e a sua forma 1. Deslocamento vector que liga a posição inicial com a posição final, de cada ponto do MC Deslocamento é “visível”, pode-se medir, pelo menos na superfície, ao contrário de tensão, que é a nossa ficção Escolhe-se ponto P, e Q na vizinhança de P Não há deformação, comportamento do corpo rígido

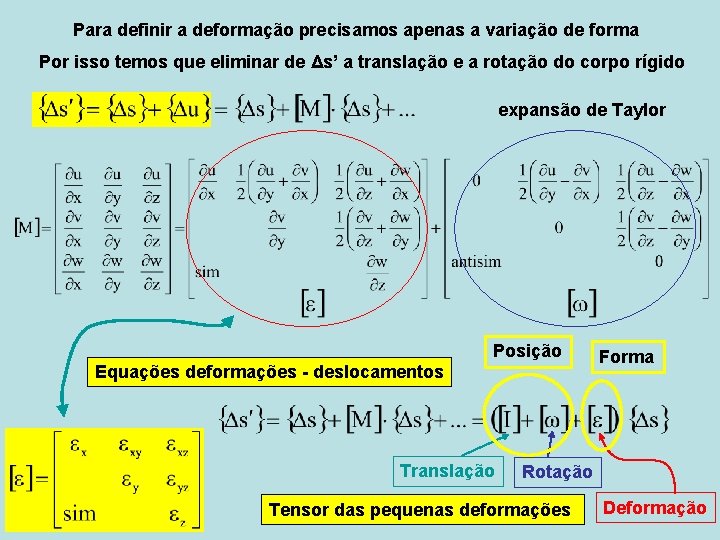
Para definir a deformação precisamos apenas a variação de forma Por isso temos que eliminar de Δs’ a translação e a rotação do corpo rígido expansão de Taylor Posição Equações deformações - deslocamentos Translação Forma Rotação Tensor das pequenas deformações Deformação

Pode-se provar o carácter tensorial do [ε] Mais ainda [ε] é tensor simétrico, como se viu da definição Pode-se usar toda a teoria desenvolvida para os tensores simétricos: Deformações principais, direcções principais, circunferência de Mohr. . . A rotação [ω] é tensor da 2ª ordem, anti-simétrico Teoria das pequenas deformações A teoria das pequenas deformações não impede deslocamentos grandes Teoria dos pequenos deslocamentos pequenas deformações Não se distingue a posição inicial e a final do MC, superfície do MC assume-se igual antes a depois da aplicação da carga, as equações de equilíbrio escrevem-se para a forma não-deformada. Chama-se 2. Teoria geometricamente linear Permite sobreposição dos efeitos As componentes de deformação não têm unidade, às vezes usa-se μ=10 -6

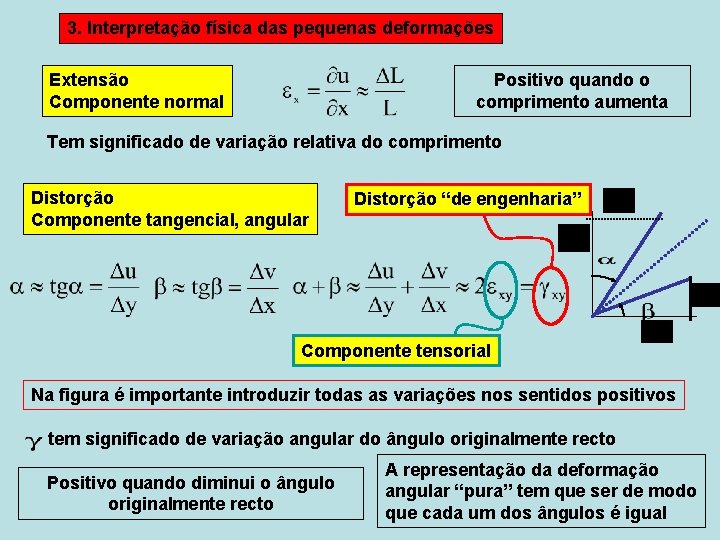
3. Interpretação física das pequenas deformações Positivo quando o comprimento aumenta Extensão Componente normal Tem significado de variação relativa do comprimento Distorção Componente tangencial, angular Distorção “de engenharia” Componente tensorial Na figura é importante introduzir todas as variações nos sentidos positivos tem significado de variação angular do ângulo originalmente recto Positivo quando diminui o ângulo originalmente recto A representação da deformação angular “pura” tem que ser de modo que cada um dos ângulos é igual

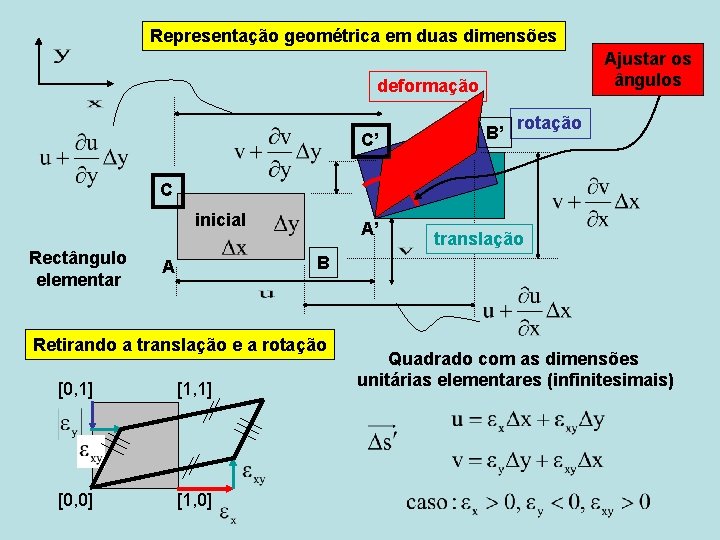
Representação geométrica em duas dimensões Ajustar os ângulos deformação C’ B’ rotação C inicial Rectângulo elementar A’ translação B A Retirando a translação e a rotação [0, 1] [1, 1] [0, 0] [1, 0] Quadrado com as dimensões unitárias elementares (infinitesimais)

4. Deformação volúmica Campo do deslocamento linear Campo de deformações uniforme Planos transformam-se para planos, rectas para rectas Referencial principal Paralelepípedo elementar: volume inicial: ngulos rectos transformam-se para ângulos rectos (distorções são nulas) Volume depois da deformação: Variação do volume: Deformação volúmica: Separação em parte volúmica e desviatórica, parte desviatórica tem o 1. invariante=0, ou seja a parte desviatórica não causa uma alteração de volume As distorções não causam alterações de volume

5. Medição das deformações: extensómetros, rosetas As medições têm que corresponder a 1 ponto ou a distribuição das deformações têm que ser uniforme Comprimento novo: L+ΔL Base de medição: L Podem-se medir apenas as extensões Sabemos: incógnitas: Devido ao sistema de coordenadas introduzido:

6. Equações de compatibilidade Equações de integrabilidade meio contínuo é contínuo depois da deformação 6 componentes da deformação versus 3 componentes do deslocamentos deformações ? ? ? deformações Mais duas equações pela substituição cíclica dos “índices” Para o estado plano Adhémar Jean Claude Barré de Saint-Venant, 1797 - 1886

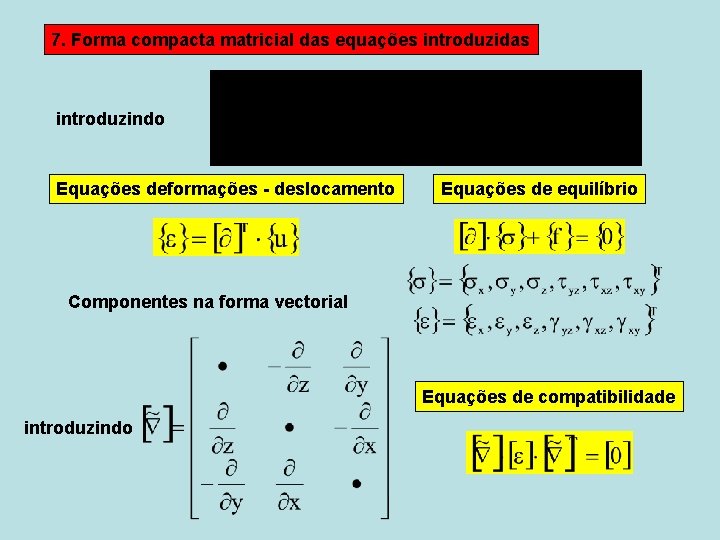
7. Forma compacta matricial das equações introduzidas introduzindo Equações deformações - deslocamento Equações de equilíbrio Componentes na forma vectorial Equações de compatibilidade introduzindo

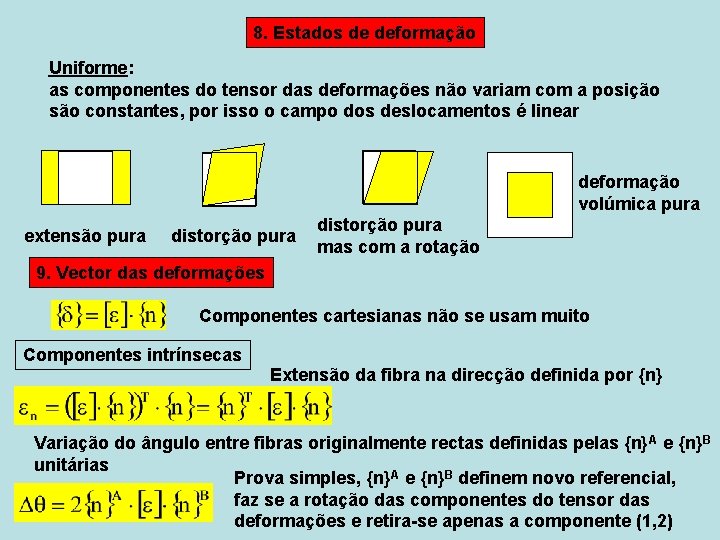
8. Estados de deformação Uniforme: as componentes do tensor das deformações não variam com a posição são constantes, por isso o campo dos deslocamentos é linear deformação volúmica pura extensão pura distorção pura mas com a rotação 9. Vector das deformações Componentes cartesianas não se usam muito Componentes intrínsecas Extensão da fibra na direcção definida por {n} Variação do ângulo entre fibras originalmente rectas definidas pelas {n} A e {n}B unitárias Prova simples, {n}A e {n}B definem novo referencial, faz se a rotação das componentes do tensor das deformações e retira-se apenas a componente (1, 2)