2 D Transformations Unit 3 Why Transformations n

2 D Transformations Unit - 3

Why Transformations? n In graphics, once we have an object described, transformations are used to move that object, scale it and rotate it

2 D Transformations y y x x y x

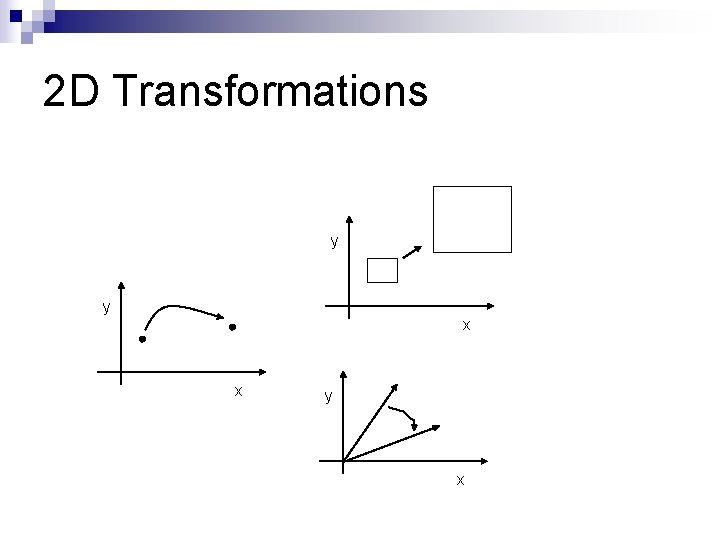
2 D Transformation n Given a 2 D object, transformation is to change the object’s ¨ Position (translation) ¨ Size (scaling) ¨ Orientation (rotation) ¨ Shapes (shear) n Apply a sequence of matrix multiplication to the object vertices

Point representation n n We can use a column vector (a 2 x 1 matrix) to represent a 2 D point x y A general form of linear transformation can be written as: x’ = ax + by + c OR y’ = dx + ey + f X’ Y’ 1 = a d 0 b e 0 c f 1 * x y 1

Translation n n Re-position a point along a straight line Given a point (x, y), and the translation distance (tx, ty) The new point: (x’, y’) x’ = x + tx y’ = y + ty OR P’ = P + T where P’ = (x’, y’) ty (x, y) x’ y’ p= x y T= tx tx ty

3 x 3 2 D Translation Matrix x’ y’ = x y + tx ty Use 3 x 1 vector x’ y’ 1 = 1 0 0 0 1 0 tx ty 1 * x y 1 § Note that now it becomes a matrix-vector multiplication

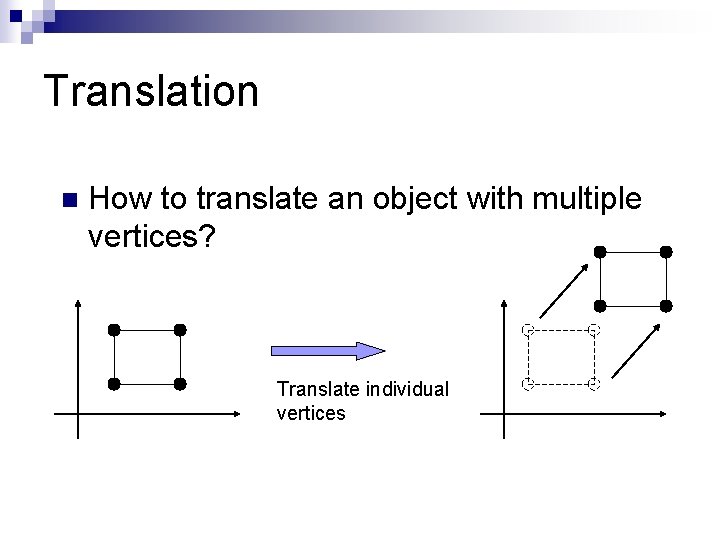
Translation n How to translate an object with multiple vertices? Translate individual vertices

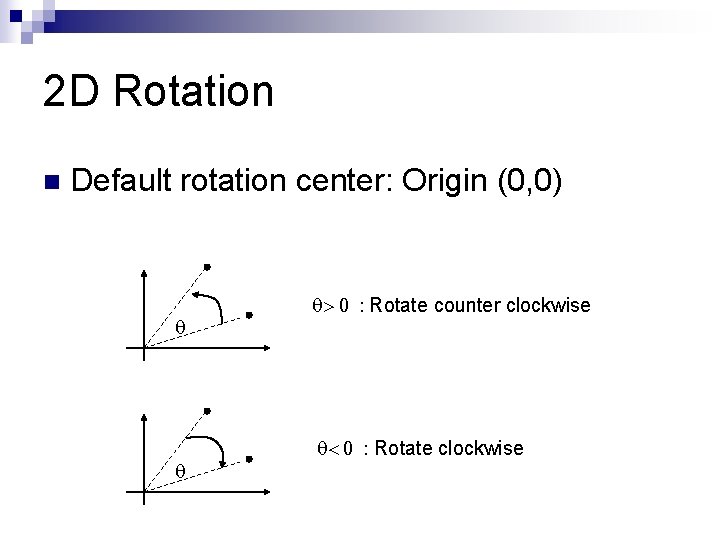
2 D Rotation n Default rotation center: Origin (0, 0) q q q> 0 : Rotate counter clockwise q< 0 : Rotate clockwise

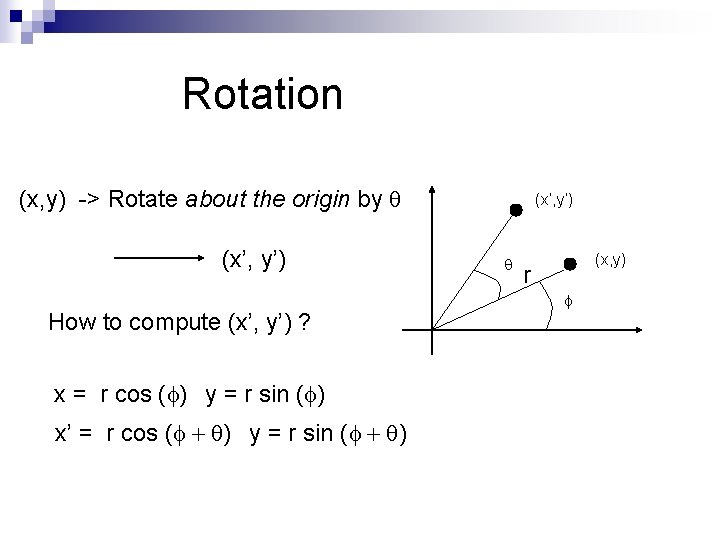
Rotation (x, y) -> Rotate about the origin by q (x’, y’) How to compute (x’, y’) ? x = r cos (f) y = r sin (f) x’ = r cos (f + q) y = r sin (f + q) (x’, y’) q (x, y) r f

Rotation (x’, y’) x = r cos (f) y = r sin (f) x’ = r cos (f + q) y = r sin (f + q) x’ = r cos (f + q) = r cos(f) cos(q) – r sin(f) sin(q) = x cos(q) – y sin(q) y’ = r sin (f + q) = r sin(f) cos(q) + r cos(f)sin(q) = y cos(q) + x sin(q) q (x, y) r f

Rotation (x’, y’) x’ = x cos(q) – y sin(q) y’ = y cos(q) + x sin(q) q (x, y) r f Matrix form? x’ y’ 3 x 3? = cos(q) sin(q) -sin(q) cos(q) x y

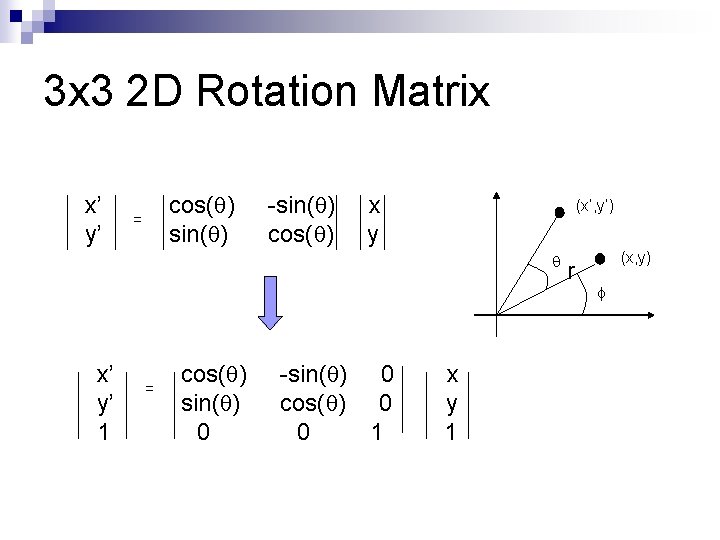
3 x 3 2 D Rotation Matrix x’ y’ cos(q) sin(q) = -sin(q) cos(q) x y (x’, y’) q x’ y’ 1 = cos(q) sin(q) 0 -sin(q) 0 cos(q) 0 0 1 x y 1 r (x, y) f

Rotation n How to rotate an object with multiple vertices? Rotate individual Vertices q

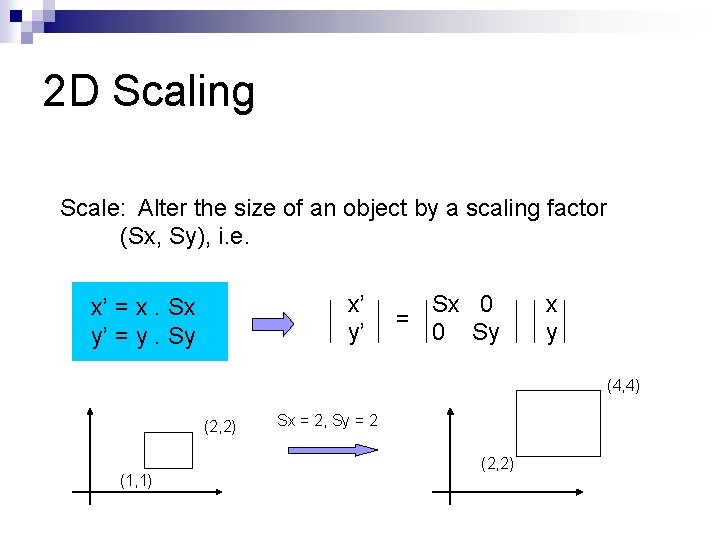
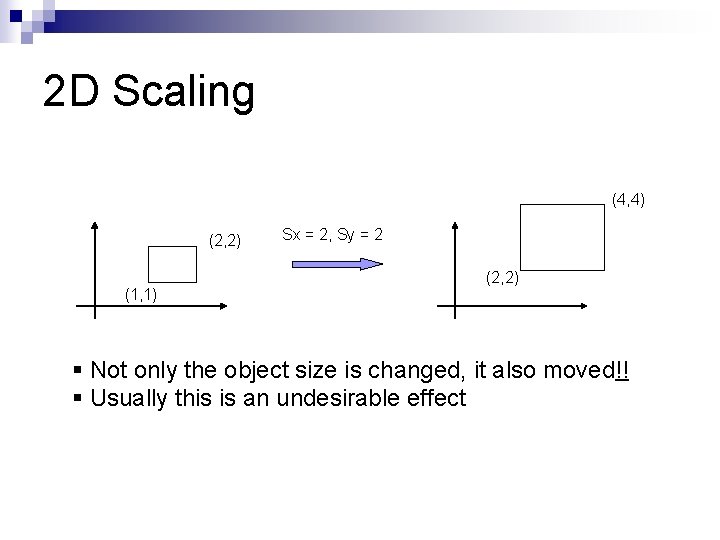
2 D Scaling Scale: Alter the size of an object by a scaling factor (Sx, Sy), i. e. x’ y’ x’ = x. Sx y’ = y. Sy Sx 0 = 0 Sy x y (4, 4) (2, 2) (1, 1) Sx = 2, Sy = 2 (2, 2)

2 D Scaling (4, 4) (2, 2) (1, 1) Sx = 2, Sy = 2 (2, 2) § Not only the object size is changed, it also moved!! § Usually this is an undesirable effect

3 x 3 2 D Scaling Matrix x’ y’ 1 = = Sx 0 0 Sy Sx 0 0 0 Sy 0 x 0 * y 1 1

Put it all together n Translation: x’ = y’ n Rotation: x’ = y’ n Scaling: x’ = y’ x + y tx ty cos(q) -sin(q) x * sin(q) cos(q) y Sx 0 0 Sy * x y

Or, 3 x 3 Matrix representations n n n Translation: Rotation: Scaling: x’ y’ 1 1 0 0 = = = 0 1 0 cos(q) sin(q) 0 Sx 0 0 Why use 3 x 3 matrices? 0 Sy 0 tx ty 1 * x y 1 -sin(q) 0 x cos(q) 0 * y 0 1 1 0 0 * 1 x y 1

Why use 3 x 3 matrices? n So that we can perform all transformations using matrix/vector multiplications n This allows us to pre-multiply all the matrices together n The point (x, y) needs to be represented as (x, y, 1) -> this is called Homogeneous coordinates!

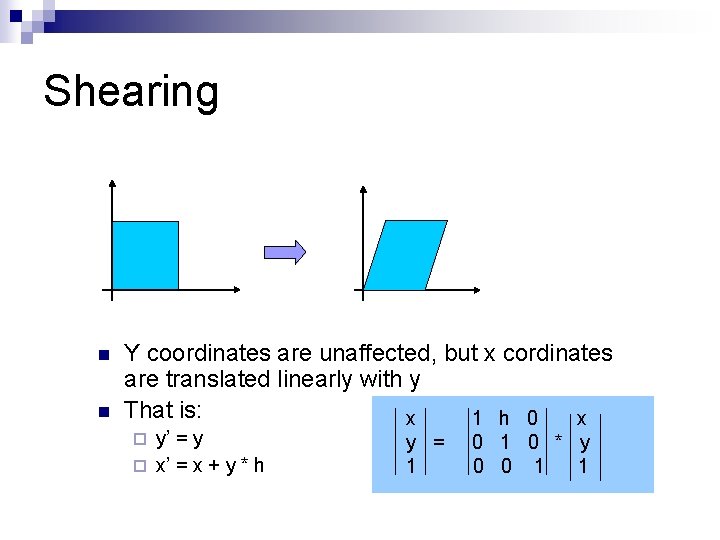
Shearing n n Y coordinates are unaffected, but x cordinates are translated linearly with y That is: x 1 h 0 x y’ = y ¨ x’ = x + y * h ¨ y = 1 0 * y 0 0 1 1

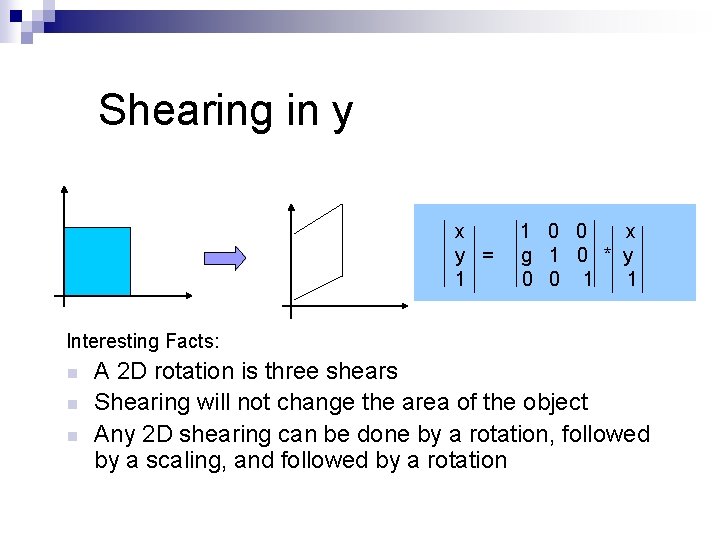
Shearing in y x y = 1 1 0 0 x g 1 0 * y 0 0 1 1 Interesting Facts: n n n A 2 D rotation is three shears Shearing will not change the area of the object Any 2 D shearing can be done by a rotation, followed by a scaling, and followed by a rotation

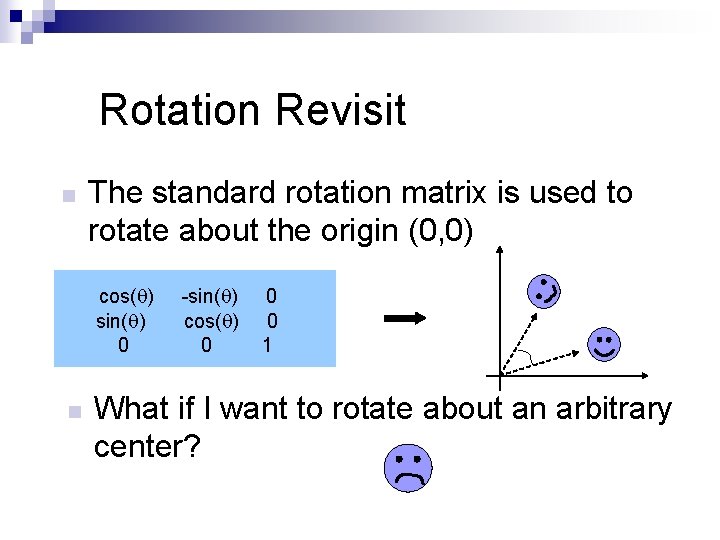
Rotation Revisit n The standard rotation matrix is used to rotate about the origin (0, 0) cos(q) sin(q) 0 n -sin(q) cos(q) 0 0 0 1 What if I want to rotate about an arbitrary center?

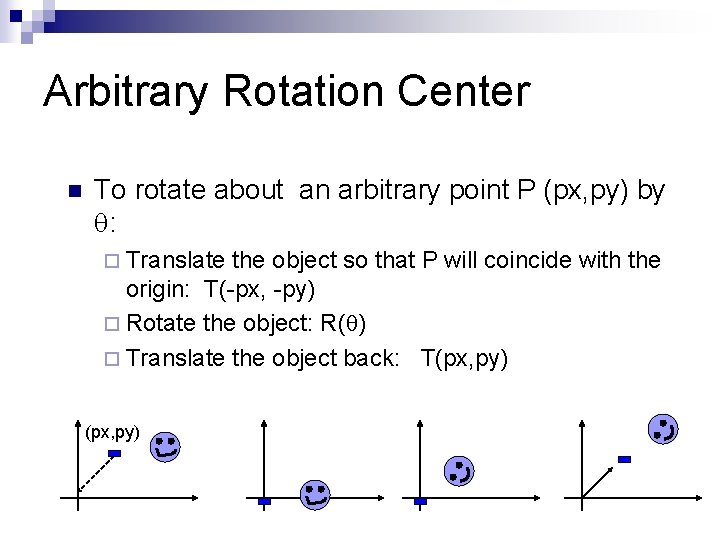
Arbitrary Rotation Center n To rotate about an arbitrary point P (px, py) by q: ¨ Translate the object so that P will coincide with the origin: T(-px, -py) ¨ Rotate the object: R(q) ¨ Translate the object back: T(px, py)

Arbitrary Rotation Center n n Translate the object so that P will coincide with the origin: T(-px, -py) Rotate the object: R(q) Translate the object back: T(px, py) Put in matrix form: x’ y’ = 1 1 0 px 0 1 py 00 1 T(px, py) R(q) T(-px, -py) cos(q) -sin(q) 0 sin(q) cos(q) 0 0 0 1 1 0 -px 0 1 -py 0 0 1 *P x y 1

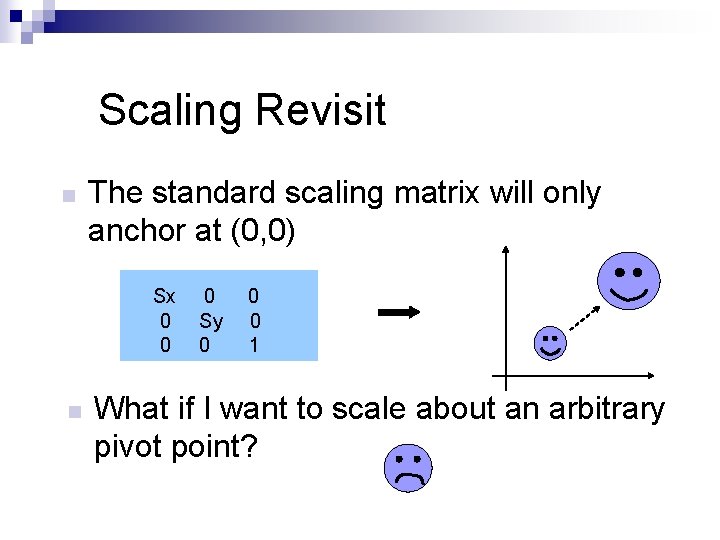
Scaling Revisit n The standard scaling matrix will only anchor at (0, 0) Sx 0 0 n 0 Sy 0 0 0 1 What if I want to scale about an arbitrary pivot point?

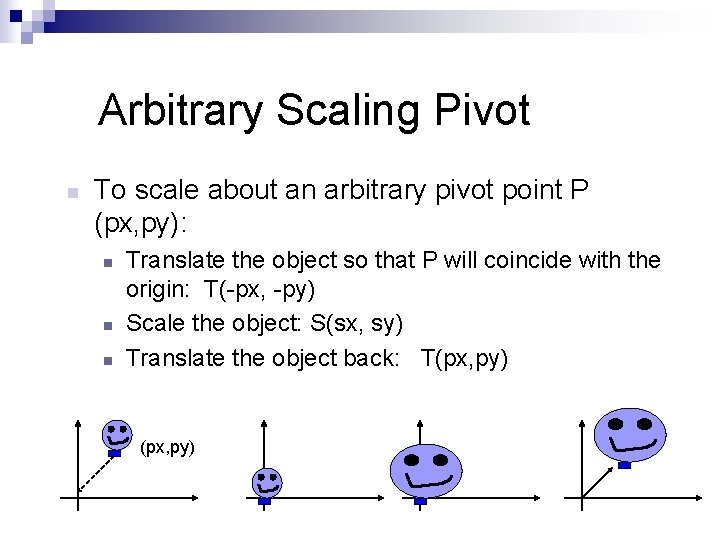
Arbitrary Scaling Pivot n To scale about an arbitrary pivot point P (px, py): n n n Translate the object so that P will coincide with the origin: T(-px, -py) Scale the object: S(sx, sy) Translate the object back: T(px, py)

Affine Transformation n n Translation, Scaling, Rotation, Shearing are all affine transformation Affine transformation – transformed point P’ (x’, y’) is a linear combination of the original point P (x, y), i. e. x’ m 11 m 12 m 13 y’ = m 21 m 22 m 23 1 0 0 1 n x y 1 Any 2 D affine transformation can be decomposed into a rotation, followed by a scaling, followed by a shearing, and followed by a translation. Affine matrix = translation x shearing x scaling x rotation

Composing Transformation n n Composing Transformation – the process of applying several transformation in succession to form one overall transformation If we apply transform a point P using M 1 matrix first, and then transform using M 2, and then M 3, then we have: (M 3 x (M 2 x (M 1 x P ))) = M 3 x M 2 x M 1 x P (pre-multiply) M

Composing Transformation n Matrix multiplication is associative M 3 x M 2 x M 1 = (M 3 x M 2) x M 1 = M 3 x (M 2 x M 1) n Transformation products may not be commutative n A x B != B x A Some cases where A x B = B x A A translation scaling rotation uniform scaling (sx = sy) B translation scaling rotation

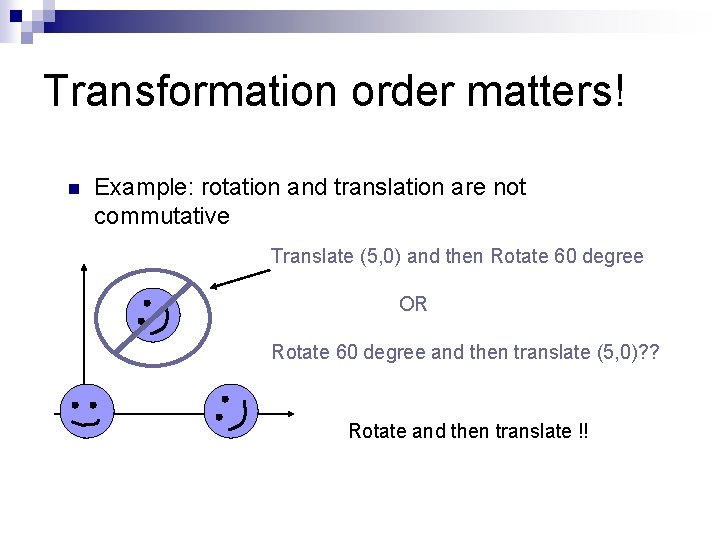
Transformation order matters! n Example: rotation and translation are not commutative Translate (5, 0) and then Rotate 60 degree OR Rotate 60 degree and then translate (5, 0)? ? Rotate and then translate !!

Inverse Transformations n Transformations can easily be reversed using inverse transformations