2 D Transformations 2 D Transformations World Coordinates

2 D Transformations

2 D Transformations • • World Coordinates Translate Rotate Scale Viewport Transforms Hierarchical Model Transforms Putting it all together

Transformations • Rigid Body Transformations - transformations that do not change the object. • Translate – If you translate a rectangle, it is still a rectangle • Scale – If you scale a rectangle, it is still a rectangle • Rotate – If you rotate a rectangle, it is still a rectangle

Vertices • We have always represented vertices as (x, y) • An alternate method is: • Example:

Matrix * Vector

Matrix * Matrix Does A*B = B*A? NO What does the identity do? AI=A

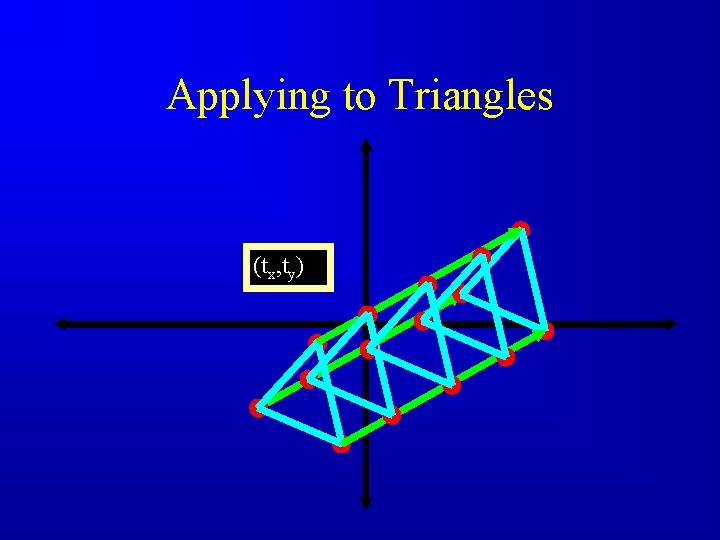
Translation • Translation - repositioning an object along a straight-line path (the translation distance) from one coordinate location to another. (x’, y’) (tx, ty) (x, y)

Translation • Given: • We want: • Matrix form:

Recall • A point is a position specified with coordinate values in some reference frame. • We usually label a point in this reference point as the origin. • All points in the reference frame are given with respect to the origin.

Applying to Triangles (tx, ty)

What do we have here? • You know how to:

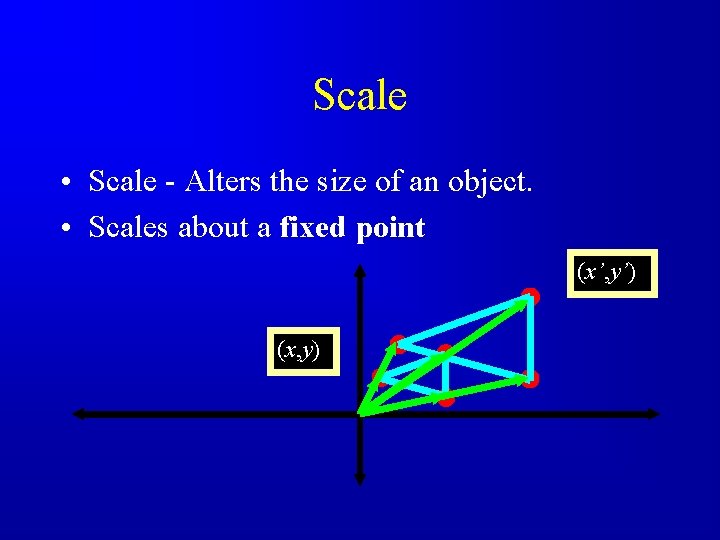
Scale • Scale - Alters the size of an object. • Scales about a fixed point (x’, y’) (x, y)

Scale • Given: • We want: • Matrix form:

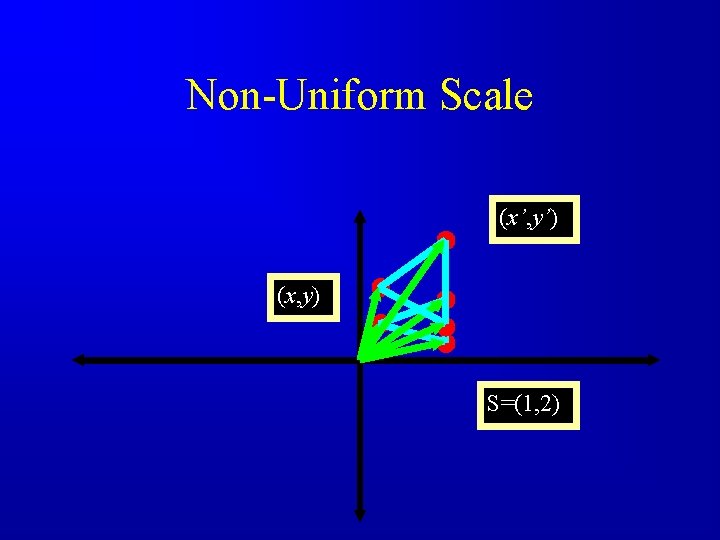
Non-Uniform Scale (x’, y’) (x, y) S=(1, 2)

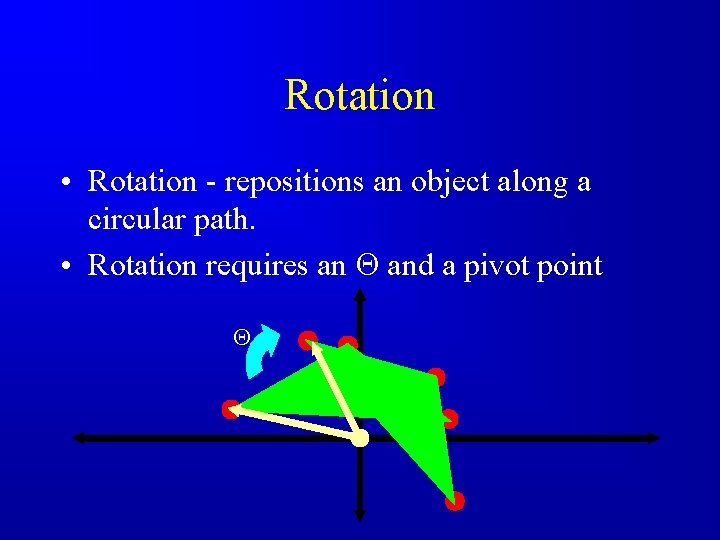
Rotation • Rotation - repositions an object along a circular path. • Rotation requires an and a pivot point

Rotation

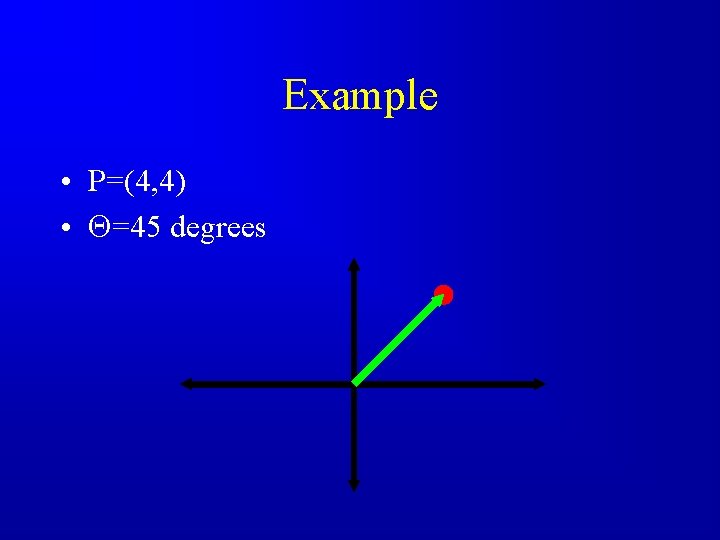
Example • P=(4, 4) • =45 degrees

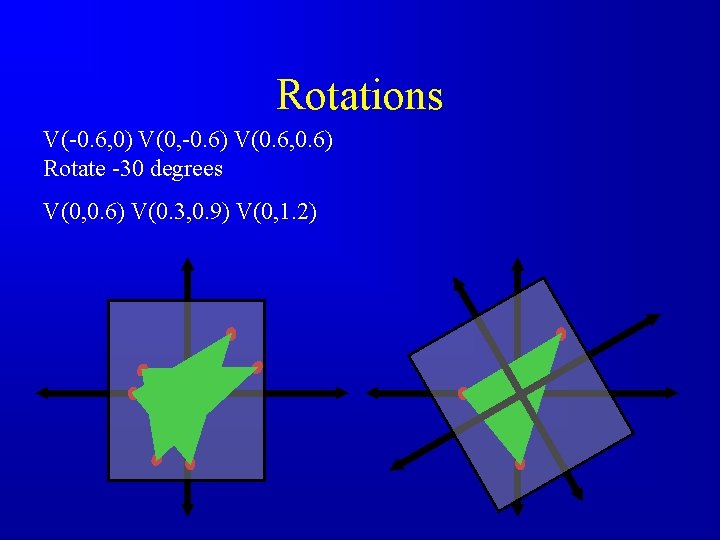
Rotations V(-0. 6, 0) V(0, -0. 6) V(0. 6, 0. 6) Rotate -30 degrees V(0, 0. 6) V(0. 3, 0. 9) V(0, 1. 2)

Combining Transformations Q: How do we specify each transformation?

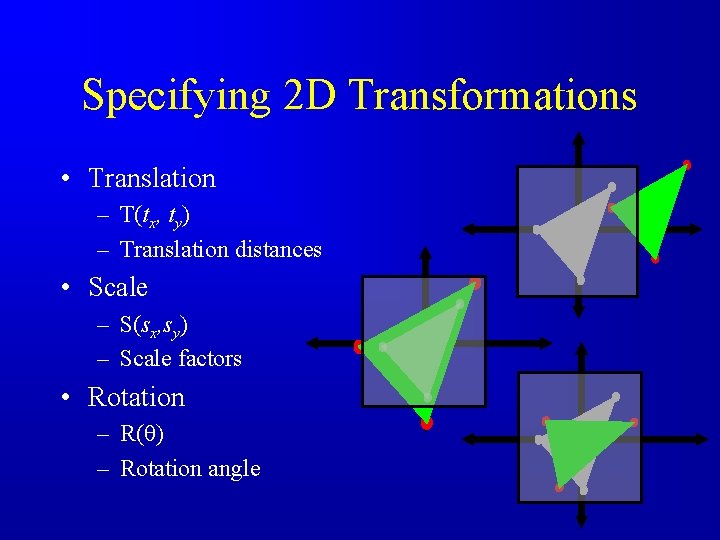
Specifying 2 D Transformations • Translation – T(tx, ty) – Translation distances • Scale – S(sx, sy) – Scale factors • Rotation – R( ) – Rotation angle

Combining Transformations • Using translate, rotation, and scale, how do we get:

Combining Transformations • Note there are two ways to combine rotation and translation. Why?

Let’s look at the equations

Combining them • We must do each step in turn. First we rotate the points, then we translate, etc. • Since we can represent the transformations by matrices, why don’t we just combine them?

2 x 2 -> 3 x 3 Matrices • We can combine transformations by expanding from 2 x 2 to 3 x 3 matrices.

Homogenous Coordinates • We need to do something to the vertices • By increasing the dimensionality of the problem we can transform the addition component of Translation into multiplication.

Homogenous Coordinates • Homogenous Coordinates - term used in mathematics to refer to the effect of this representation on Cartesian equations. Converting a pt(x, y) and f(x, y)=0 -> (xh, yh, h) then in homogenous equations mean (v*xh, v*yh, v*h) can be factored out. • What you should get: By expressing the transformations with homogenous equations and coordinates, all transformations can be expressed as matrix multiplications.

Final Transformations Compare Equations

Combining Transformations

How would we get:

How would we get:

Coordinate Systems • Object Coordinates • World Coordinates • Eye Coordinates

Object Coordinates

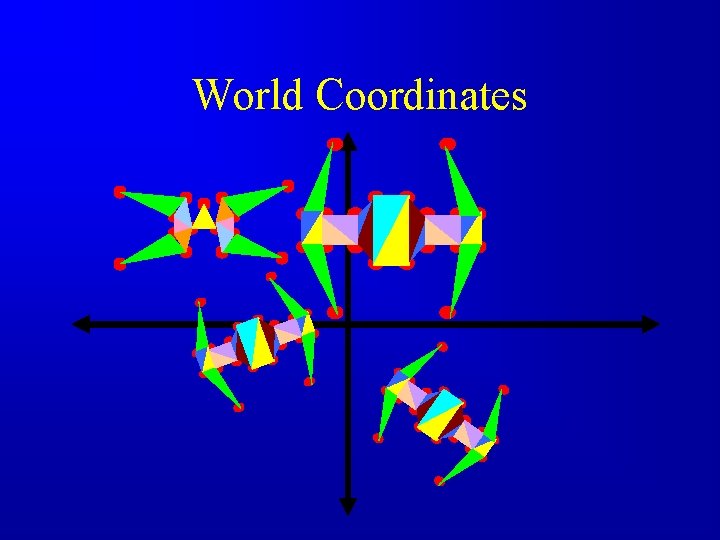
World Coordinates

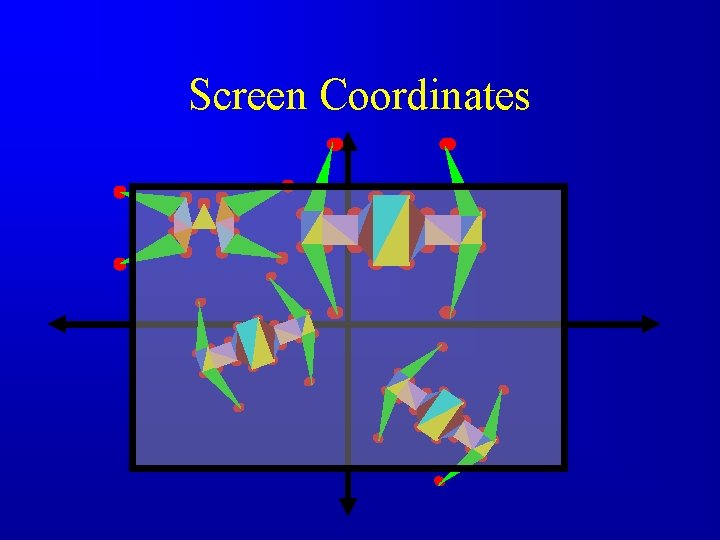
Screen Coordinates

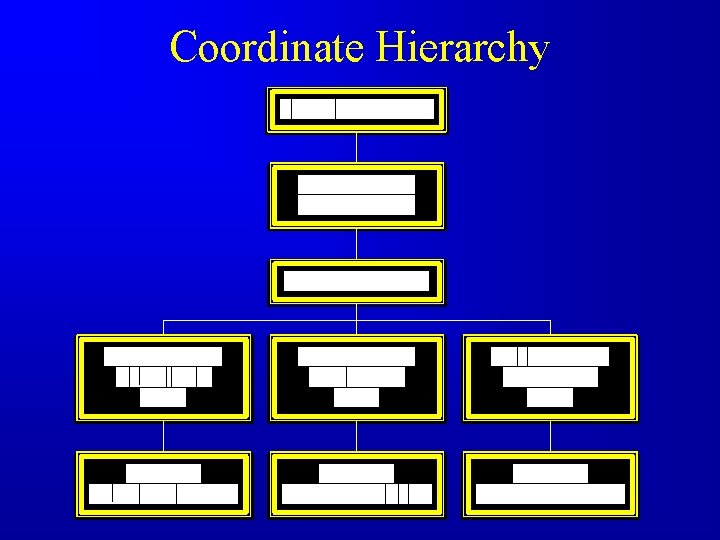
Coordinate Hierarchy

Let’s reexamine assignment 1

Transformation Hierarchies • (See chapter 10 for details) • For example, a robot arm

Transformation Hierarchies • Let’s examine:

Transformation Hierarchies • What is a better way?

Transformation Hierarchies • What is a better way?

World Coordinates Transformation Hierarchies • We can have transformations be in relation to each other Transformation: Upper Arm -> World Upper Arm Coordinates Transformation: Lower -> Upper Lower Arm Coordinates Transformation: Hand-> Lower Hand Coordinates

Rotation about a Fixed Point Start with identity matrix: C I Move fixed point to origin: C CT Rotate: C CR Move fixed point back: C CT -1 Result: C = TR T – 1 which is backwards – Cp This result is a consequence of doing postmultiplications. Let’s try again. 44 Angel: Interactive Computer Graphics 5 E © Addison-Wesley 2009

Reversing the Order We want C = T – 1 R T so we must do the operations in the following order C I C CT -1 C CR C CT Each operation corresponds to one function call in the program. Note that the last operation specified is the first executed in the program 45 Angel: Interactive Computer Graphics 5 E © Addison-Wesley 2009

Open. GL Example • Rotation about z axis by 30 degrees with a fixed point of (1. 0, 2. 0, 3. 0) gl. Matrix. Mode(GL_MODELVIEW); gl. Load. Identity(); gl. Translatef(1. 0, 2. 0, 3. 0); gl. Rotatef(30. 0, 1. 0); gl. Translatef(-1. 0, -2. 0, -3. 0); gl. Begin(GL_TRIANGLES); . . . • Remember that last transform specified in the program is the first applied 46 Angel: Interactive Computer Graphics 5 E © Addison-Wesley 2009

Matrix Stacks • In many situations we want to save transformation matrices for use later – Traversing hierarchical data structures (Chapter 10) – Avoiding state changes when executing display lists • Open. GL maintains stacks for each type of matrix – Access present type (as set by gl. Matrix. Mode) by gl. Push. Matrix() gl. Pop. Matrix() 47 Angel: Interactive Computer Graphics 5 E © Addison-Wesley 2009