2 D shallow water model III Sverdrup balance

2 D shallow water model III Sverdrup balance Keywords • subtropical gyre • potential vorticity • trapezoidal integration

Subtropical gyre Mean sea level [cm]

3 Shallow water model • We consider the 3 -demensional linear equations on the Arakawa C grid

4 Setting • The all boundaries are the land • Parameter setting ▫ grid size: 100 km ▫ number of x-grid: 48 ▫ number of y-grid: 38 ▫ time: 100 second and 40000 steps ▫ plain (f 0 =10‒ 4 second‒ 1 and =10‒ 11 second‒ 1 m‒ 1) ▫ depth: 5000 m ▫ : 10‒ 6 second‒ 1 ▫ Initial condition: h = u = v = 0

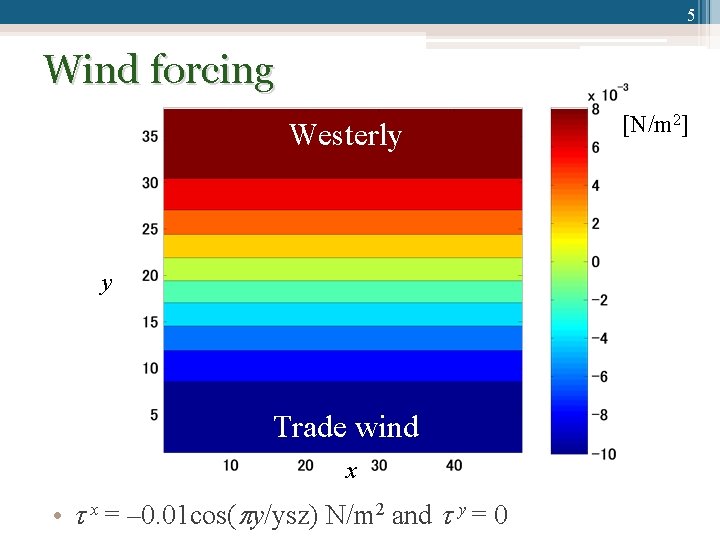
5 Wind forcing Westerly y Trade wind x • x = ‒ 0. 01 cos( y/ysz) N/m 2 and y = 0 [N/m 2]

6 Result thickness anomaly [cm] y x

7 Result thickness anomaly y western boundary current x [cm]

8 Double gyre zonal wind stress [N/m 2] thickness anomaly y Subarctic gyre x y Subtropical gyre x [cm]

9 Analytical solution • First, we consider the steady state solution (i. e. , the final state) (1) (2) (3) • We take x(2) – y(1) and substitute that into (3)

10 Analytical solution relative vorticity • The equation that is zero is called the Sverdrup balance • Positive (negative) wind stress curl causes northward (southward) flow in the Northern Hemisphere

11 Sverdrup transport V: Sverdrup transport • By zonally integrating this equation, the transport of the western boundary current can be estimated • Along y =19 in the model ▫ Vwbc= 3. 1 106 m 3/s = 3. 1 Sv ▫ RHS = ‒ 4. 1 106 m 3/s

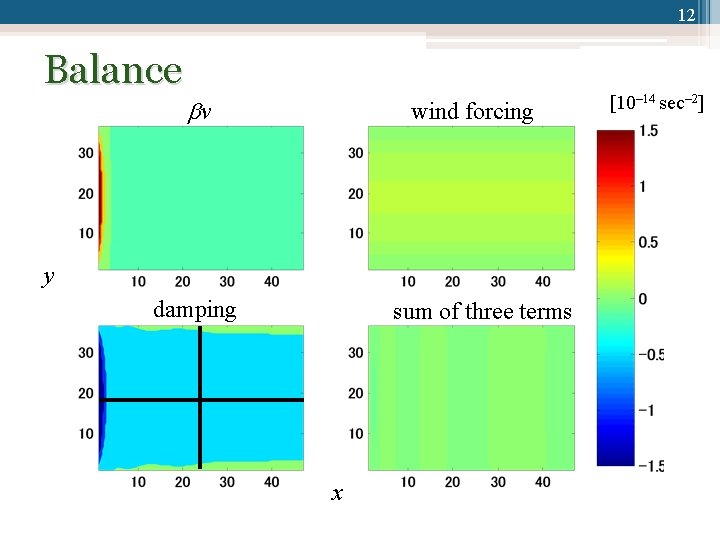
12 Balance v wind forcing y damping sum of three terms x [10‒ 14 sec‒ 2]

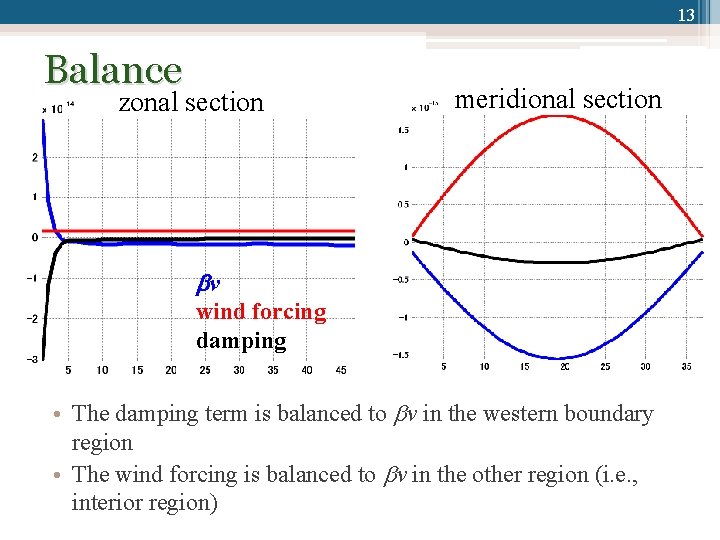
13 Balance zonal section meridional section v wind forcing damping • The damping term is balanced to v in the western boundary region • The wind forcing is balanced to v in the other region (i. e. , interior region)

14 Balance • Domain average ▫ v: 1. 7 10 19 ▫ wind forcing: 1. 1 10 15 ▫ damping: 6. 0 10 16 • The wind forcing is balanced to the damping • The circulation should be clockwise to achieve the balance • If is small, the clockwise circulation becomes strong

15 Parameter sensitivity thickness anomaly [cm] y =10‒ 6 =10‒ 5 x • A smaller damping parameter results in stronger circulation =10‒ 7

16 Potential vorticity • For physical interpretation, we introduce potential vorticity (4) (5) (6) • To this end, we take x(5) – y(4) and substitute into (6) (7)

17 Potential vorticity • Recalling that the nonlinear terms are ignored, the equation (7) is equivalent to (8) potential vorticity (PV) • Hence, if there is no wind forcing and damping, PV is conserved with the flow

18 Potential vorticity • In the steady state, the equation (8) is identical to • Thus, this equation indicates the vorticity balance as follows: 1. Advection of planetary vorticity 2. Vorticity input by wind forcing 3. damping of relative vorticity

19 Potential vorticity 1. In the interior region (Sverdrup balance) ▫ The wind forcing inputs the vorticity ▫ The meridional flow removes the vorticity 2. In the western boundary region ▫ The western boundary current carries the vorticity ▫ The damping reduces the vorticity 3. In the entire domain ▫ The wind forcing inputs the vorticity ▫ The damping reduces the vorticity

20 Rossby wave • The PV conservation is tightly related to the Rossby wave • In the linear framework, • If the geostrophic balance is assumed, then

21 Rossby wave • We substitute the wave solution as follows: • The corresponding dispersion equation is • This is the same with the dispersion relation of Rossby wave • Thus, during the propagation of the Rossby wave, PV is conserved 1. temporal thickness change 2. temporal relative vorticity change 3. meridional advection of planetary vorticity

22 Rossby wave 1. Short wave (Ld 2(k 2 + l 2) >> 1) ▫ The second term is balanced to the third term 2. Long wave (Ld 2(k 2 + l 2) << 1) ▫ The first term is balanced to the third term ▫ The relative vorticity can be ignored

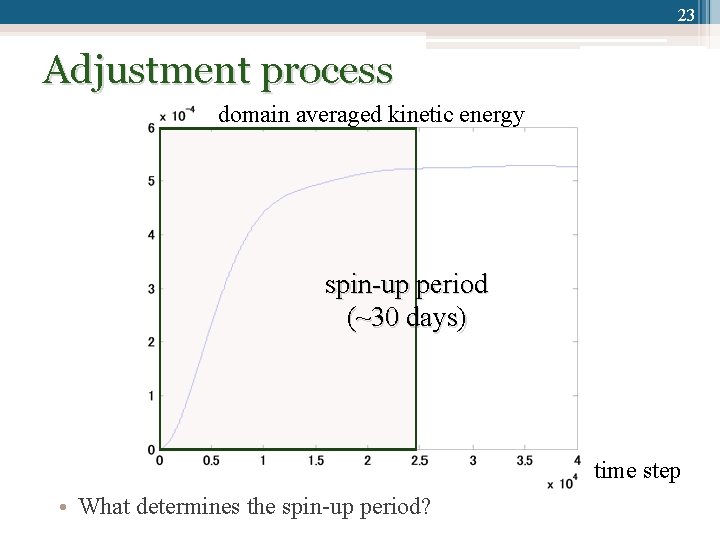
23 Adjustment process domain averaged kinetic energy spin-up period (~30 days) time step • What determines the spin-up period?

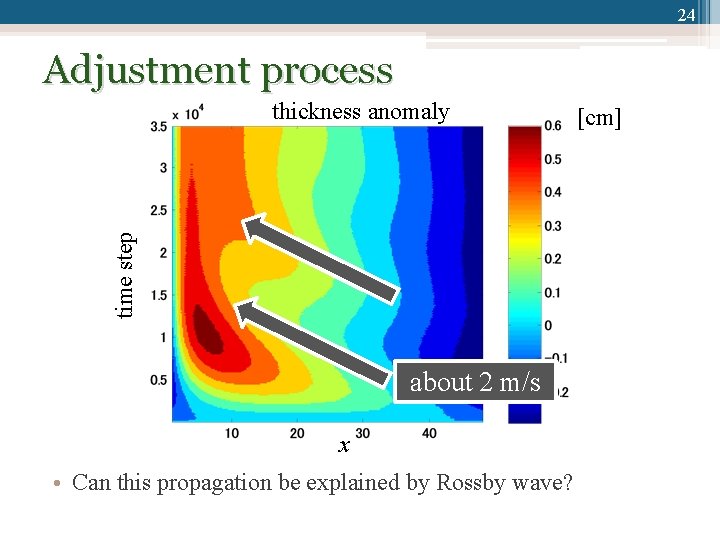
24 Adjustment process time step thickness anomaly about 2 m/s x • Can this propagation be explained by Rossby wave? [cm]

25 Group velocity of Rossby wave • We estimate this value as follows: ▫ k: 2 /(2*4800 km) ▫ l: 2 /(3800 km) • Cgx = ‒ 2. 2 m/s (westward propagation) • The group velocity of the Rossby wave determines the adjustment time of the ocean circulation

26 Group velocity of Rossby wave • If the model is a 1. 5 layer and we use the following parameters ▫ g : 0. 03 m/s 2 ▫ H: 1000 m • Cgx = ‒ 3. 0 cm/s (westward propagation) • In this case, it takes about 10 years to finish the adjustment of ocean circulation

27 Integration • Transport V between x 1 and x 2 can be estimated as where dimension is as follows: V [m 3/s], x [m], h [m], and v [m/s] • How do we estimate this value numerically?

28 Trapezoidal integration • If x 2 x 1 is small, by using the Taylor expansion, Trapezoidal integration

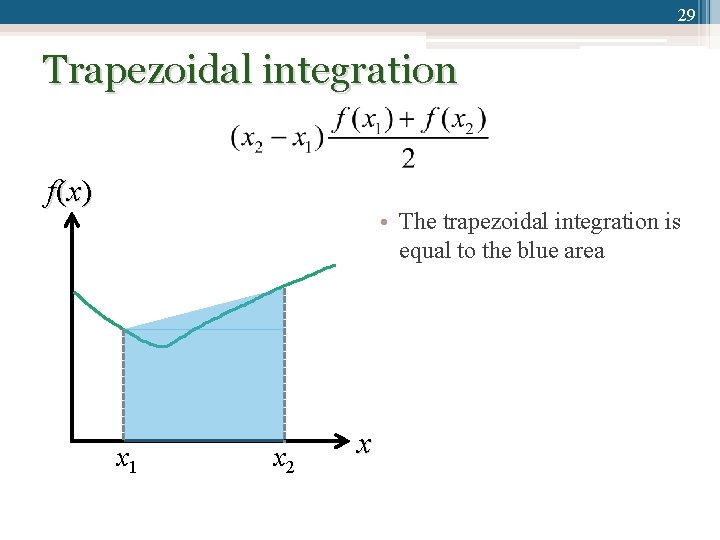
29 Trapezoidal integration f (x ) • The trapezoidal integration is equal to the blue area x 1 x 2 x

30 Trapezoidal integration • Because x 2 x 1 is not always small, the domain is divided by N where we apply the Trapezoidal integration for each integration • The error is smaller, when dx is smaller