2 Analyzing TwoVariable Data Lesson 2 6 The

2 Analyzing Two-Variable Data Lesson 2. 6 The Least-Squares Regression Line Statistics and Probability with Applications, 3 rd Edition Starnes & Tabor Bedford Freeman Worth Publishers

The Least-Squares Regression Line Learning Targets After this lesson, you should be able to: ü Calculate the equation of the least-squares regression line using technology. ü Calculate the equation of the least-squares regression line using summary statistics. ü Describe how outliers affect the least-squares regression line. Statistics and Probability with Applications, 3 rd Edition 2

The Least-Squares Regression Line A good regression line makes the residuals as small as possible, so that the predicted values are close to the actual values. For this reason, statisticians prefer using the least-squares regression line. Least-Squares Regression Line The least-squares regression line is the line that makes the sum of the squared residuals as small as possible. Statistics and Probability with Applications, 3 rd Edition 3
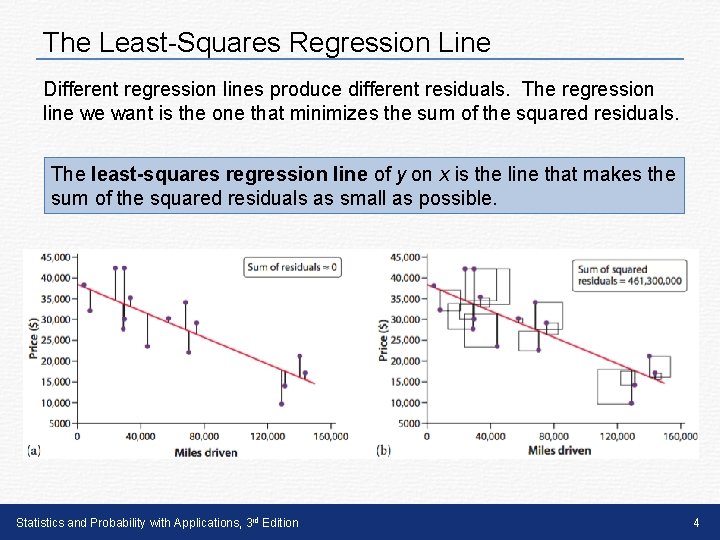
The Least-Squares Regression Line Different regression lines produce different residuals. The regression line we want is the one that minimizes the sum of the squared residuals. The least-squares regression line of y on x is the line that makes the sum of the squared residuals as small as possible. Statistics and Probability with Applications, 3 rd Edition 4

Does taller mean faster? Calculating the least-squares regression line • Height (ft) 116. 5 51. 8 305. 0 72. 2 205. 0 195. 0 124. 6 Statistics and Probability with Applications, 3 rd Edition Maximum Speed (mph) 47. 0 35. 0 90. 0 46. 6 71. 0 67. 0 43. 5 5

The Least-Squares Regression Line It is possible to calculate the equation of the least-squares regression line using the means and standard deviations of each variable, along with their correlation. How to calculate the least-squares regression line using summary statistics Statistics and Probability with Applications, 3 rd Edition 6

How expensive is a Dodge Charger? Calculating the least-squares regression line using summary statistics • Statistics and Probability with Applications, 3 rd Edition 7
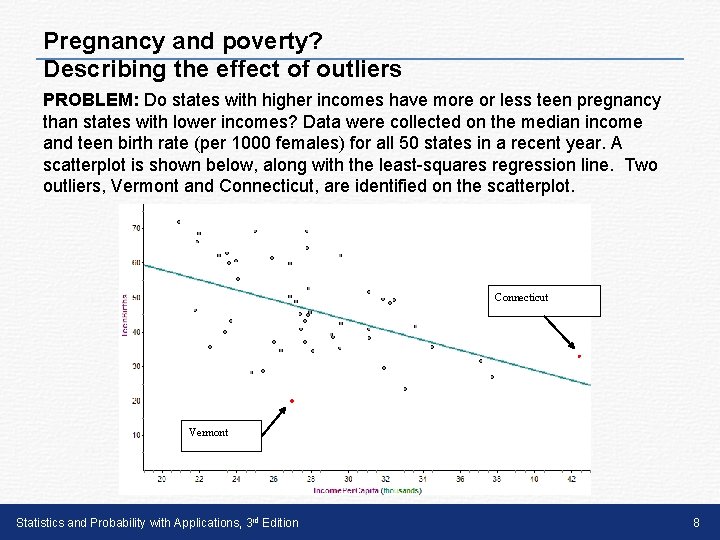
Pregnancy and poverty? Describing the effect of outliers PROBLEM: Do states with higher incomes have more or less teen pregnancy than states with lower incomes? Data were collected on the median income and teen birth rate (per 1000 females) for all 50 states in a recent year. A scatterplot is shown below, along with the least-squares regression line. Two outliers, Vermont and Connecticut, are identified on the scatterplot. Connecticut Vermont Statistics and Probability with Applications, 3 rd Edition 8
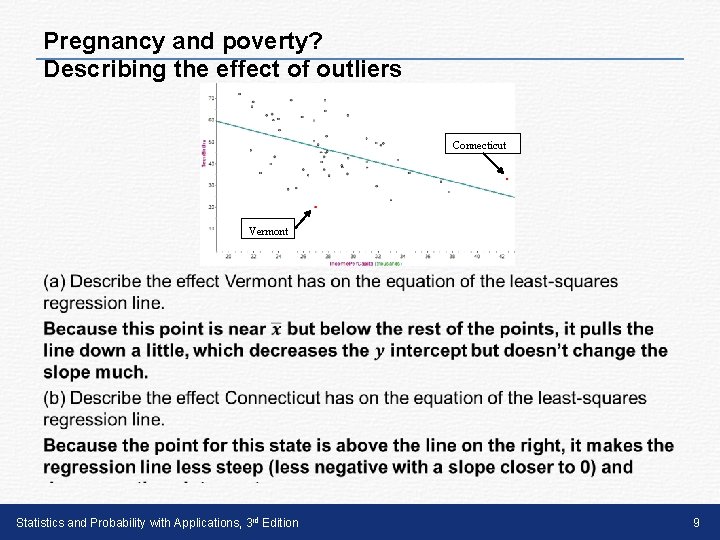
Pregnancy and poverty? Describing the effect of outliers • Connecticut Vermont Statistics and Probability with Applications, 3 rd Edition 9
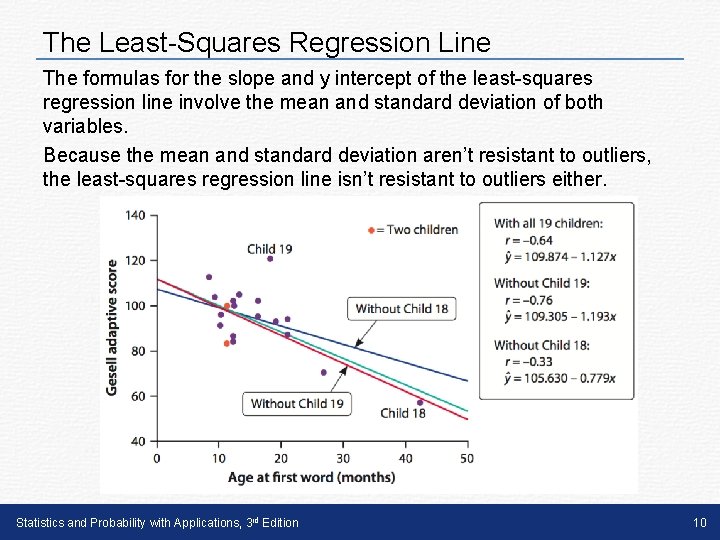
The Least-Squares Regression Line The formulas for the slope and y intercept of the least-squares regression line involve the mean and standard deviation of both variables. Because the mean and standard deviation aren’t resistant to outliers, the least-squares regression line isn’t resistant to outliers either. Statistics and Probability with Applications, 3 rd Edition 10
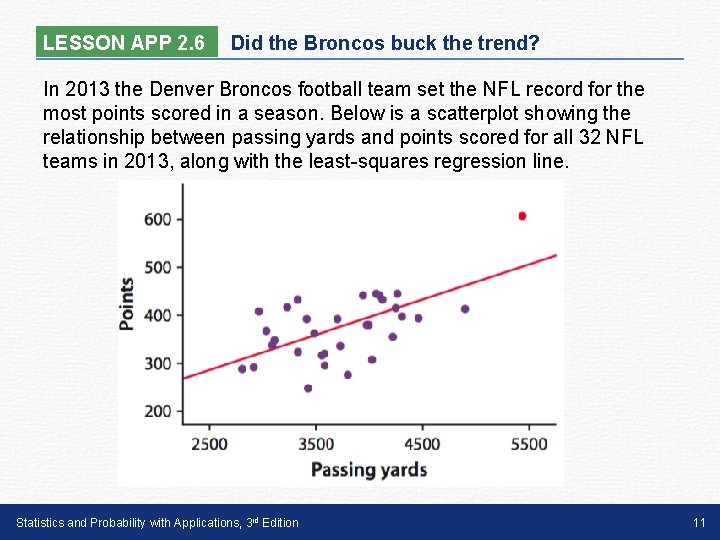
LESSON APP 2. 6 Did the Broncos buck the trend? In 2013 the Denver Broncos football team set the NFL record for the most points scored in a season. Below is a scatterplot showing the relationship between passing yards and points scored for all 32 NFL teams in 2013, along with the least-squares regression line. Statistics and Probability with Applications, 3 rd Edition 11

LESSON APP 2. 6 Did the Broncos buck the trend? 1. For passing yards, the mean is 3770 yards, with a standard deviation of 594 yards. For points scored, the mean is 375 points, with a standard deviation of 70 points. The correlation between passing yards and points scored is r = 0. 616. Use this information to calculate the equation of the least-squares regression line. 2. The point for the Denver Broncos is highlighted in red. What effect does this point have on the equation of the least-squares regression line? Explain. Statistics and Probability with Applications, 3 rd Edition 12

LESSON APP 2. 6 Did the Broncos buck the trend? 1. For passing yards, the mean is 3770 yards, with a standard deviation of 594 yards. For points scored, the mean is 375 points, with a standard deviation of 70 points. The correlation between passing yards and points scored is r = 0. 616. Use this information to calculate the equation of the least-squares regression line. Statistics and Probability with Applications, 3 rd Edition 13

LESSON APP 2. 6 Did the Broncos buck the trend? 2. The point for the Denver Broncos is highlighted in red. What effect does this point have on the equation of the least-squares regression line? Explain. Statistics and Probability with Applications, 3 rd Edition 14

The Least-Squares Regression Line Learning Targets After this lesson, you should be able to: ü Calculate the equation of the least-squares regression line using technology. ü Calculate the equation of the least-squares regression line using summary statistics. ü Describe how outliers affect the least-squares regression line. Statistics and Probability with Applications, 3 rd Edition 15
- Slides: 15