2 9 AbsoluteValue Functions Section 2 9 Absolute

2 -9 Absolute–Value Functions Section 2. 9 Absolute Value Functions Holt Algebra 2

2 -9 Absolute–Value Functions The absolute-value parent function is composed of two linear pieces, one with a slope of – 1 and one with a slope of 1. In Lesson 2 -6, you transformed linear functions. You can also transform absolutevalue functions. Holt Algebra 2

2 -9 Absolute–Value Functions Translating Absolute-Value Functions Perform the transformation on f(x) = |x|. Then graph the transformed function g(x). 5 units down f(x) = |x| g(x) = f(x) + k g(x) = |x| – 5 g(x) Substitute. The graph of g(x) = |x| – 5 is the graph of f(x) = |x| after a vertical shift of 5 units down. The vertex of g(x) is (0, – 5). Holt Algebra 2

2 -9 Absolute–Value Functions Because the entire graph moves when shifted, the shift from f(x) = |x| determines the vertex of an absolute-value graph. Holt Algebra 2

2 -9 Absolute–Value Functions Translations of an Absolute-Value Function Translate f(x) = |x| so that the vertex is at (– 1, – 3). Then graph. g(x) = |x – h| + k f(x) g(x) = |x – (– 1)| + (– 3) g(x) = |x + 1| – 3 g(x) Holt Algebra 2

2 -9 Absolute–Value Functions Absolute-value functions can also be stretched, compressed, and reflected. Remember! Reflection across x-axis: g(x) = –f(x) Reflection across y-axis: g(x) = f(–x) Remember! Vertical stretch and compression : g(x) = af(x) Horizontal stretch and compression: g(x) = f Holt Algebra 2

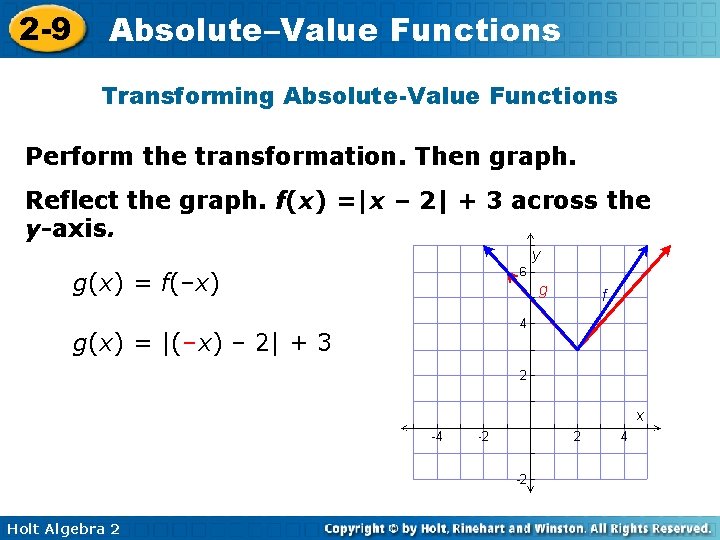
2 -9 Absolute–Value Functions Transforming Absolute-Value Functions Perform the transformation. Then graph. Reflect the graph. f(x) =|x – 2| + 3 across the y-axis. g(x) = f(–x) g(x) = |(–x) – 2| + 3 Holt Algebra 2 g f

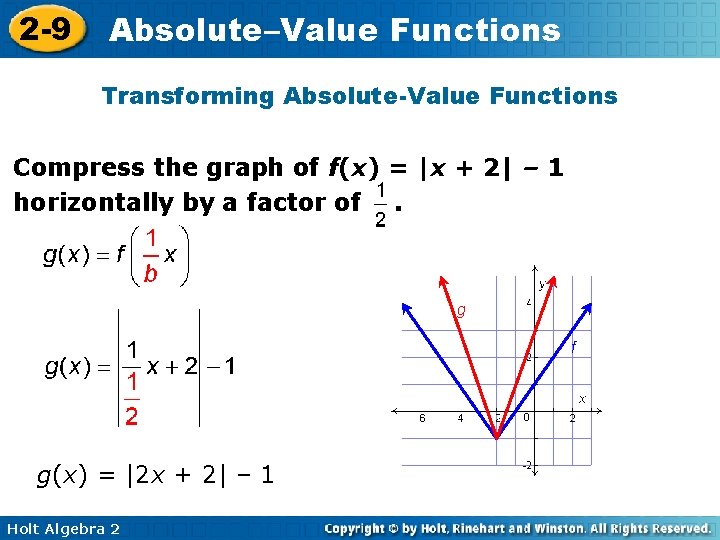
2 -9 Absolute–Value Functions Transforming Absolute-Value Functions Compress the graph of f(x) = |x + 2| – 1 horizontally by a factor of. g f g(x) = |2 x + 2| – 1 Holt Algebra 2