2 9 AbsoluteValue Functions Objective Graph and transform

2 -9 Absolute–Value Functions Objective Graph and transform absolute-value functions. An absolute-value function is a function whose rule contains an absolute-value expression. The graph of the parent absolute-value function f(x) = |x| has a V shape with a minimum point or vertex at (0, 0). Holt Algebra 2

2 -9 Absolute–Value Functions The absolute-value parent function is composed of two linear pieces, one with a slope of – 1 and one with a slope of 1. In Lesson 2 -6, you transformed linear functions. You can also transform absolutevalue functions. Holt Algebra 2

2 -9 Absolute–Value Functions Remember! The general forms for translations are Vertical: g(x) = f(x) + k Horizontal: g(x) = f(x – h) Holt Algebra 2

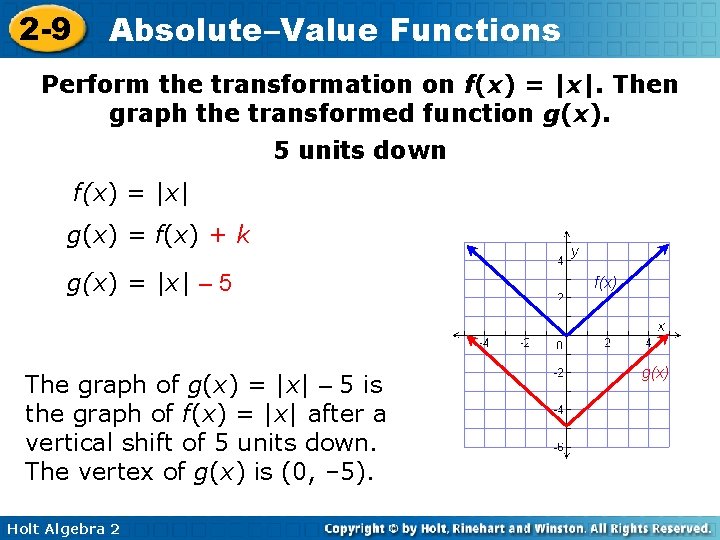
2 -9 Absolute–Value Functions Perform the transformation on f(x) = |x|. Then graph the transformed function g(x). 5 units down f(x) = |x| g(x) = f(x) + k g(x) = |x| – 5 The graph of g(x) = |x| – 5 is the graph of f(x) = |x| after a vertical shift of 5 units down. The vertex of g(x) is (0, – 5). Holt Algebra 2 f(x) g(x)

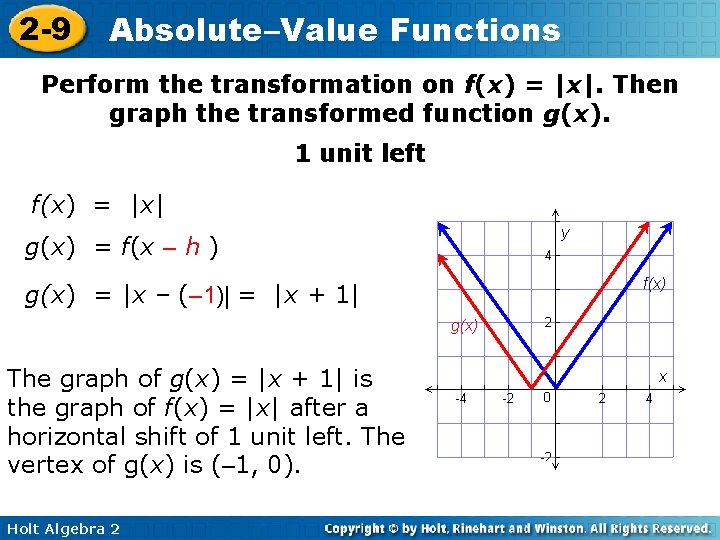
2 -9 Absolute–Value Functions Perform the transformation on f(x) = |x|. Then graph the transformed function g(x). 1 unit left f(x) = |x| g(x) = f(x – h ) f(x) g(x) = |x – (– 1)| = |x + 1| g(x) The graph of g(x) = |x + 1| is the graph of f(x) = |x| after a horizontal shift of 1 unit left. The vertex of g(x) is (– 1, 0). Holt Algebra 2

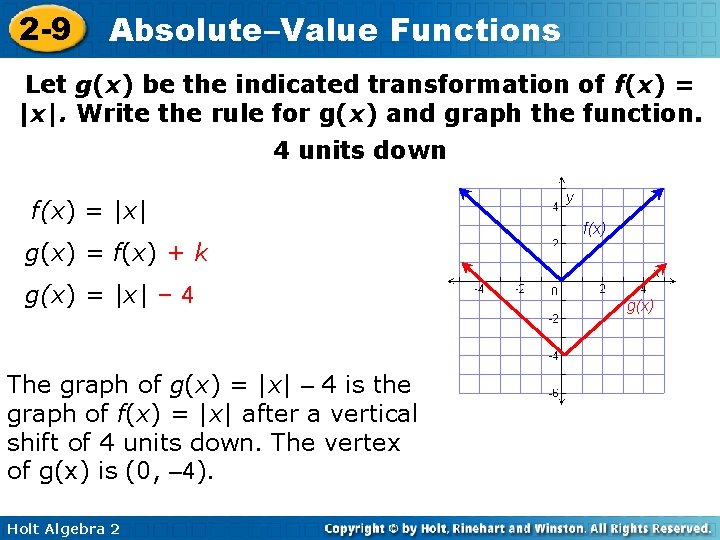
2 -9 Absolute–Value Functions Let g(x) be the indicated transformation of f(x) = |x|. Write the rule for g(x) and graph the function. 4 units down f(x) = |x| f(x) g(x) = f(x) + k g(x) = |x| – 4 The graph of g(x) = |x| – 4 is the graph of f(x) = |x| after a vertical shift of 4 units down. The vertex of g(x) is (0, – 4). Holt Algebra 2 g(x)

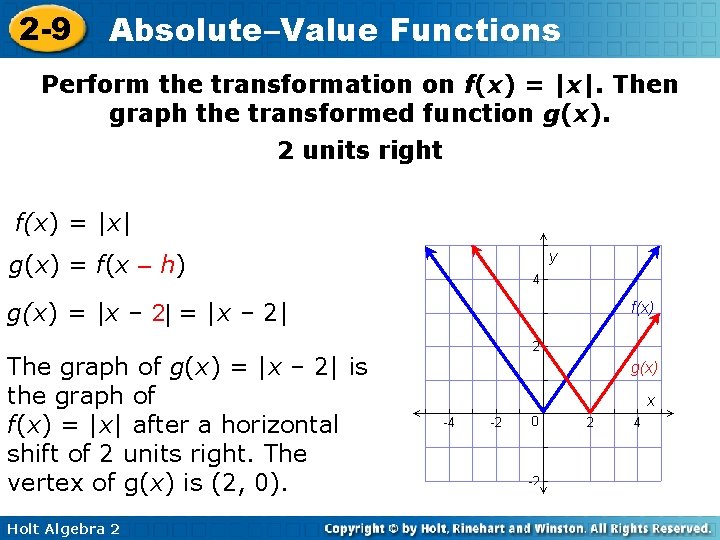
2 -9 Absolute–Value Functions Perform the transformation on f(x) = |x|. Then graph the transformed function g(x). 2 units right f(x) = |x| g(x) = f(x – h) g(x) = |x – 2| f(x) The graph of g(x) = |x – 2| is the graph of f(x) = |x| after a horizontal shift of 2 units right. The vertex of g(x) is (2, 0). g(x) Holt Algebra 2

2 -9 Absolute–Value Functions Because the entire graph moves when shifted, the shift from f(x) = |x| determines the vertex of an absolute-value graph. Holt Algebra 2

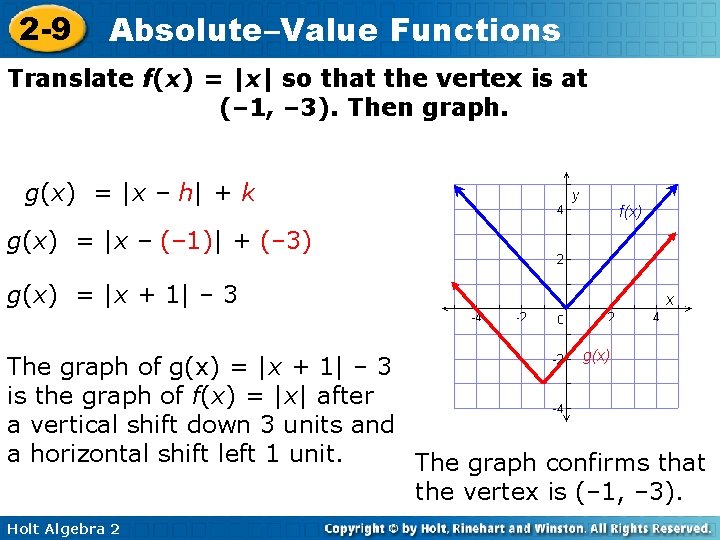
2 -9 Absolute–Value Functions Translate f(x) = |x| so that the vertex is at (– 1, – 3). Then graph. g(x) = |x – h| + k f(x) g(x) = |x – (– 1)| + (– 3) g(x) = |x + 1| – 3 g(x) The graph of g(x) = |x + 1| – 3 is the graph of f(x) = |x| after a vertical shift down 3 units and a horizontal shift left 1 unit. The graph confirms that the vertex is (– 1, – 3). Holt Algebra 2

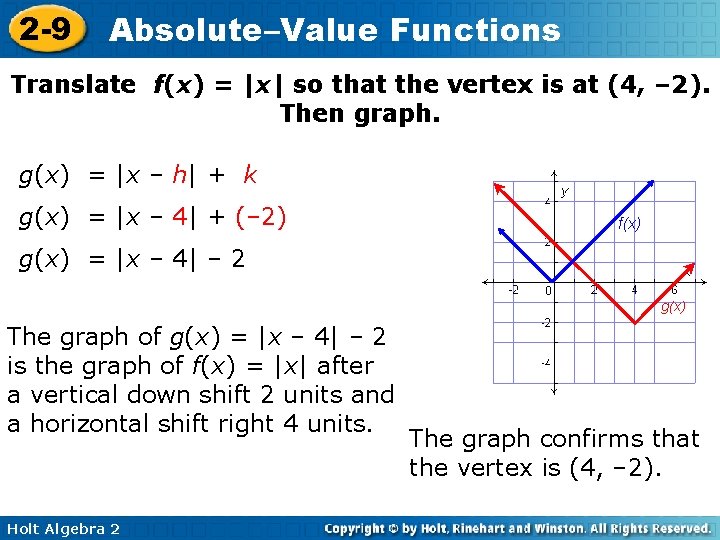
2 -9 Absolute–Value Functions Translate f(x) = |x| so that the vertex is at (4, – 2). Then graph. g(x) = |x – h| + k g(x) = |x – 4| + (– 2) f(x) g(x) = |x – 4| – 2 g(x) The graph of g(x) = |x – 4| – 2 is the graph of f(x) = |x| after a vertical down shift 2 units and a horizontal shift right 4 units. Holt Algebra 2 The graph confirms that the vertex is (4, – 2).

2 -9 Absolute–Value Functions Absolute-value functions can also be stretched, compressed, and reflected. Remember! Reflection across x-axis: g(x) = –f(x) Reflection across y-axis: g(x) = f(–x) Remember! Vertical stretch and compression : g(x) = af(x) Horizontal stretch and compression: g(x) = f Holt Algebra 2

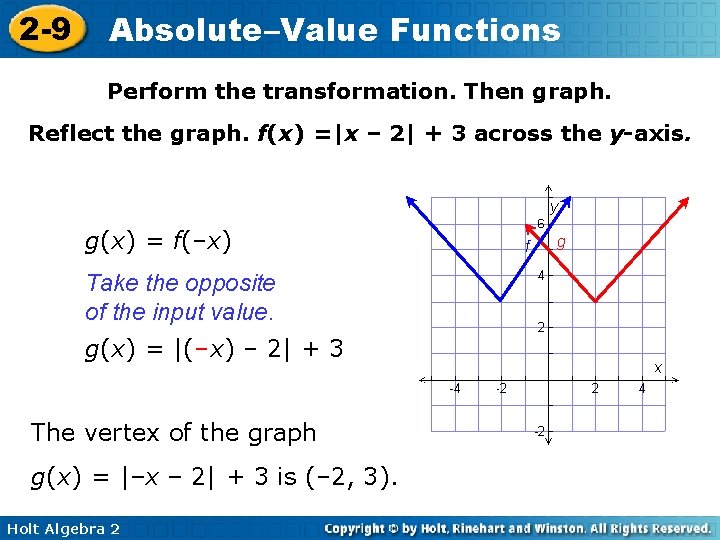
2 -9 Absolute–Value Functions Perform the transformation. Then graph. Reflect the graph. f(x) =|x – 2| + 3 across the y-axis. g(x) = f(–x) Take the opposite of the input value. g(x) = |(–x) – 2| + 3 The vertex of the graph g(x) = |–x – 2| + 3 is (– 2, 3). Holt Algebra 2 f g

2 -9 Absolute–Value Functions Stretch the graph. f(x) = |x| – 1 vertically by a factor of 2. g(x) = af(x) g(x) = 2(|x| – 1) Multiply the entire function by 2. g(x) = 2|x| – 2 The graph of g(x) = 2|x| – 2 is the graph of f(x) = |x| – 1 after a vertical stretch by a factor of 2. The vertex of g is at (0, – 2). Holt Algebra 2

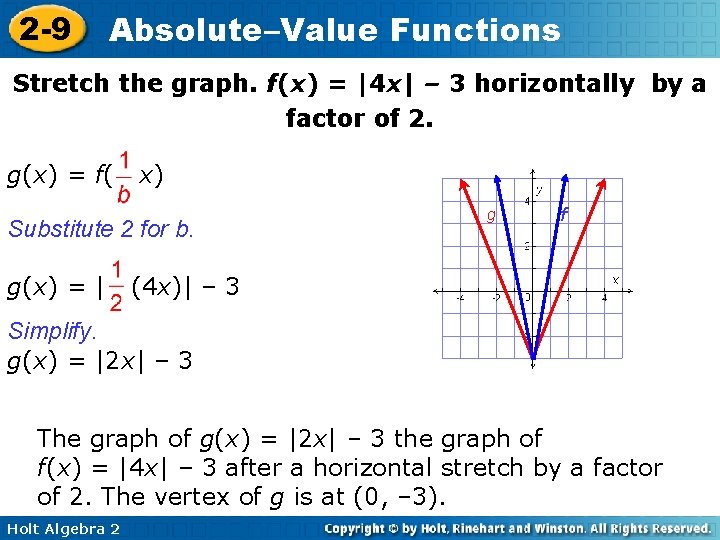
2 -9 Absolute–Value Functions Stretch the graph. f(x) = |4 x| – 3 horizontally by a factor of 2. g(x) = f( x) Substitute 2 for b. g(x) = | g f (4 x)| – 3 Simplify. g(x) = |2 x| – 3 The graph of g(x) = |2 x| – 3 the graph of f(x) = |4 x| – 3 after a horizontal stretch by a factor of 2. The vertex of g is at (0, – 3). Holt Algebra 2

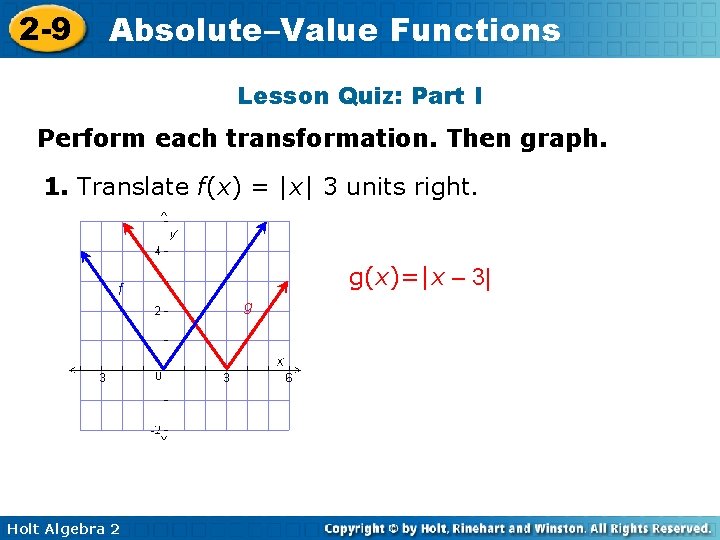
2 -9 Absolute–Value Functions Lesson Quiz: Part I Perform each transformation. Then graph. 1. Translate f(x) = |x| 3 units right. g(x)=|x – 3| f g Holt Algebra 2

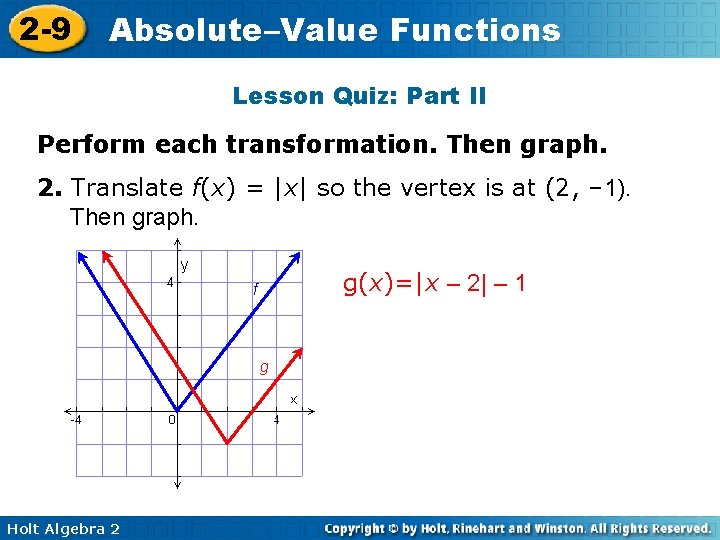
2 -9 Absolute–Value Functions Lesson Quiz: Part II Perform each transformation. Then graph. 2. Translate f(x) = |x| so the vertex is at (2, – 1). Then graph. g(x)=|x – 2| – 1 f g Holt Algebra 2

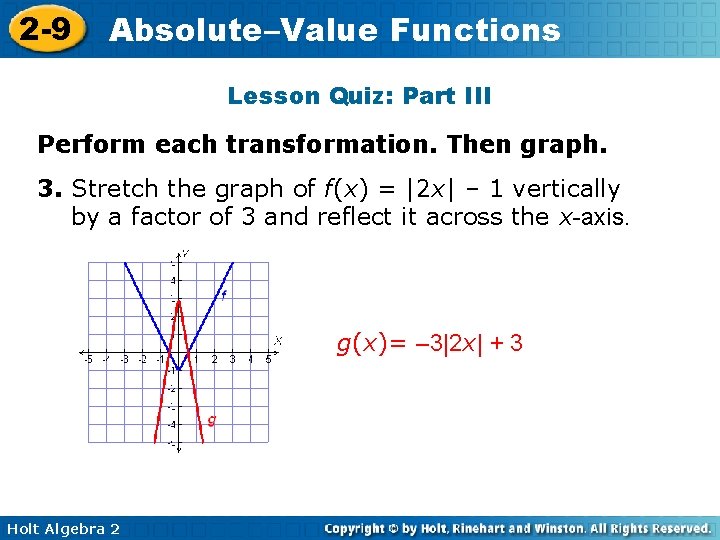
2 -9 Absolute–Value Functions Lesson Quiz: Part III Perform each transformation. Then graph. 3. Stretch the graph of f(x) = |2 x| – 1 vertically by a factor of 3 and reflect it across the x-axis. g(x)= – 3|2 x| + 3 Holt Algebra 2