2 9 AbsoluteValue Functions LEARNING GOALS FOR LESSON

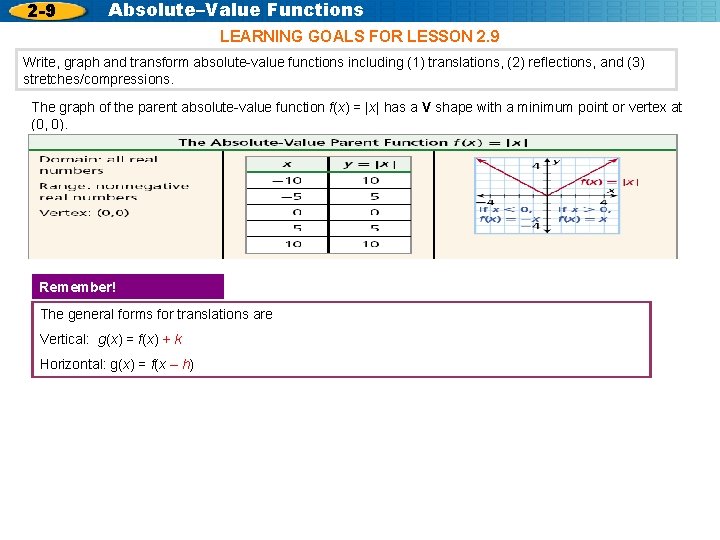
2 -9 Absolute–Value Functions LEARNING GOALS FOR LESSON 2. 9 Write, graph and transform absolute-value functions including (1) translations, (2) reflections, and (3) stretches/compressions. The graph of the parent absolute-value function f(x) = |x| has a V shape with a minimum point or vertex at (0, 0). Remember! The general forms for translations are Vertical: g(x) = f(x) + k Horizontal: g(x) = f(x – h)

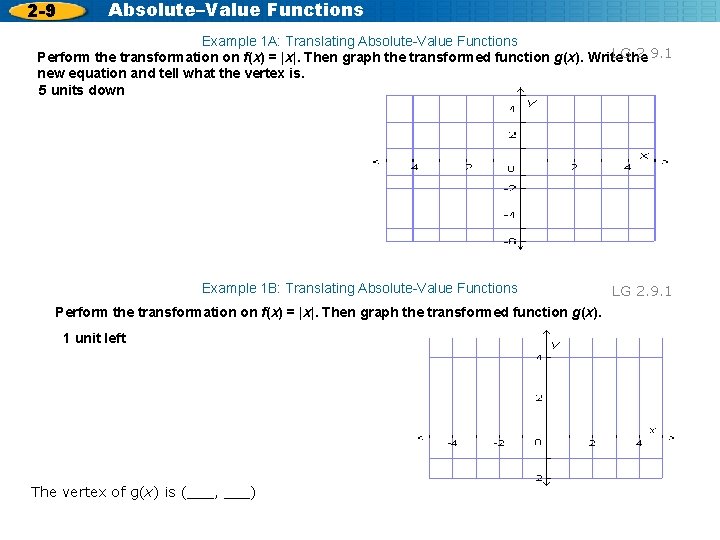
2 -9 Absolute–Value Functions Example 1 A: Translating Absolute-Value Functions LGthe 2. 9. 1 Perform the transformation on f(x) = |x|. Then graph the transformed function g(x). Write new equation and tell what the vertex is. 5 units down Example 1 B: Translating Absolute-Value Functions Perform the transformation on f(x) = |x|. Then graph the transformed function g(x). 1 unit left The vertex of g(x) is (___, ___) LG 2. 9. 1

2 -9 Absolute–Value Functions Example 1 C: Translations of an Absolute-Value Function Translate f(x) = |x| so that the vertex is at (– 1, – 3). Then graph. Check Yourself! Translate f(x) = |x| so that the vertex is at (4, – 2). Then graph. LG 2. 9. 1

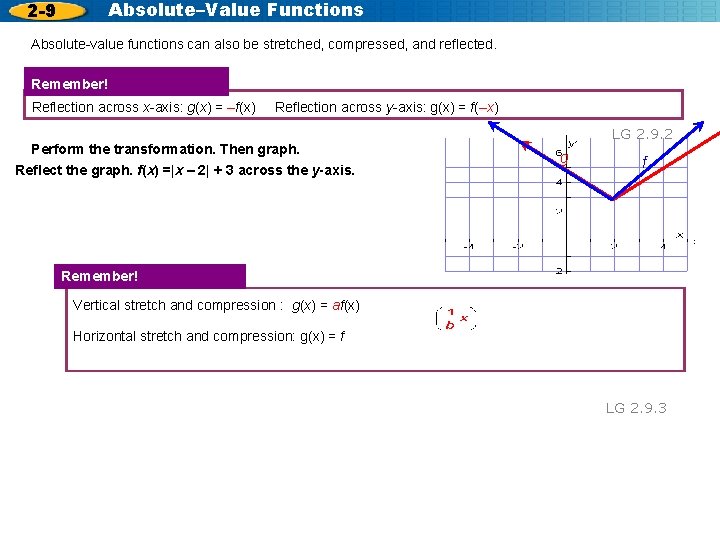
Absolute–Value Functions 2 -9 Absolute-value functions can also be stretched, compressed, and reflected. Remember! Reflection across x-axis: g(x) = –f(x) Reflection across y-axis: g(x) = f(–x) Perform the transformation. Then graph. Reflect the graph. f(x) =|x – 2| + 3 across the y-axis. LG 2. 9. 2 g f Remember! Vertical stretch and compression : g(x) = af(x) Horizontal stretch and compression: g(x) = f LG 2. 9. 3

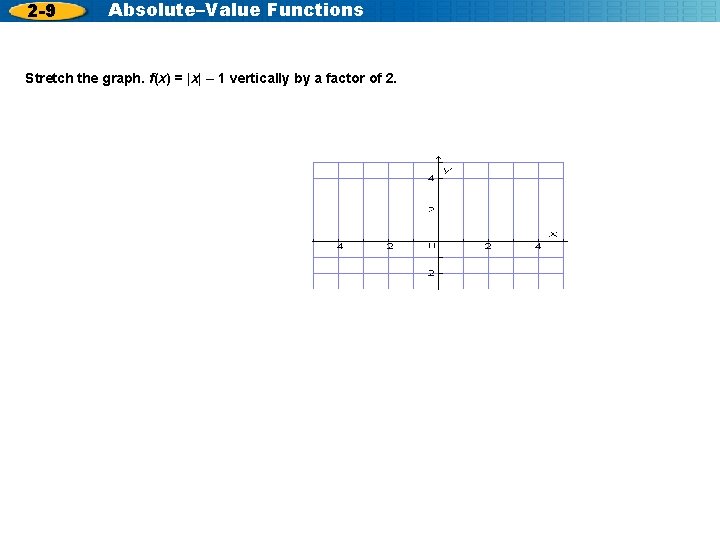
2 -9 Absolute–Value Functions Stretch the graph. f(x) = |x| – 1 vertically by a factor of 2.

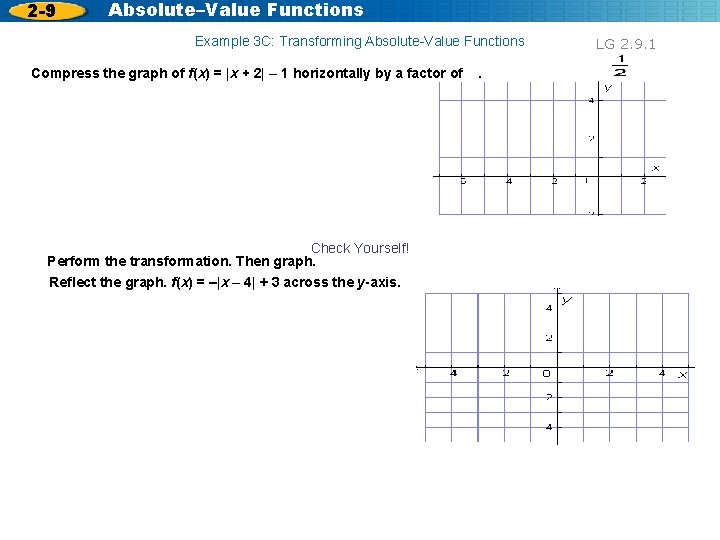
2 -9 Absolute–Value Functions Example 3 C: Transforming Absolute-Value Functions Compress the graph of f(x) = |x + 2| – 1 horizontally by a factor of Check Yourself! Perform the transformation. Then graph. Reflect the graph. f(x) = –|x – 4| + 3 across the y-axis. . LG 2. 9. 1

2 -9 Absolute–Value Functions Lesson Quiz: Part I Perform each transformation. Then graph. 1. Translate f(x) = |x| 3 units right. 2. Translate f(x) = |x| so the vertex is at (2, – 1). 3. Stretch the graph of f(x) = |2 x| – 1 vertically by a factor of 3 and reflect it across the x-axis.