2 8 Solving Equations in One Variable 2

2. 8 Solving Equations in One Variable 2. 9 Solving Inequalities in One Variable After completing this lesson, you should be able to: üSolve equations involving fractions using both algebraic and graphical techniques üIdentify extraneous solutions üSolve inequalities involving polynomial and rational functions using both algebraic and graphical techniques.

Consider this … • What strategy would you use to solve 3 = 2 x___? x+2 3 x + 1 • What strategy would you use to solve 3 + 2 x___ ≤ 0 ? x+2 3 x + 1

Rational Equation - equations involving rational expressions or fractions § In most cases we solve rational equations by multiplying by the least common denominator. § If the LCD contains a variable, this may result in an equation of which the solutions are not solutions to the original equation which are referred to as extraneous solutions (really aren’t solutions!!)

Ex 1 Solve each equation algebraically. Confirm graphically and identify any extraneous solutions. a) x + 5 = 14 x b)

Ex 1 Solve each equation algebraically. Confirm graphically and identify any extraneous solutions. a) 3 + 6 = 3 -x x + 2 x 2 + 2 x x b) 3 x + 1 = x+5 x– 2 7 x 2 + 3 x - 10

Find the dimensions of the rectangle with minimum perimeter if its area is 200 square meters. Find this least perimeter.

Polynomial Inequalities • Every polynomial inequality can be expressed in such a way that f(x) is on one side of an inequality symbol (≤, ≥, >, <) and 0 on the other. Solving Polynomial Inequalities • To solve f(x) > 0, find values of x which make f(x) positive. • To solve f(x) < 0, find values of x which make f(x) negative. • A sign chart can be an easy way to identify the value of x which solve a polynomial inequality.
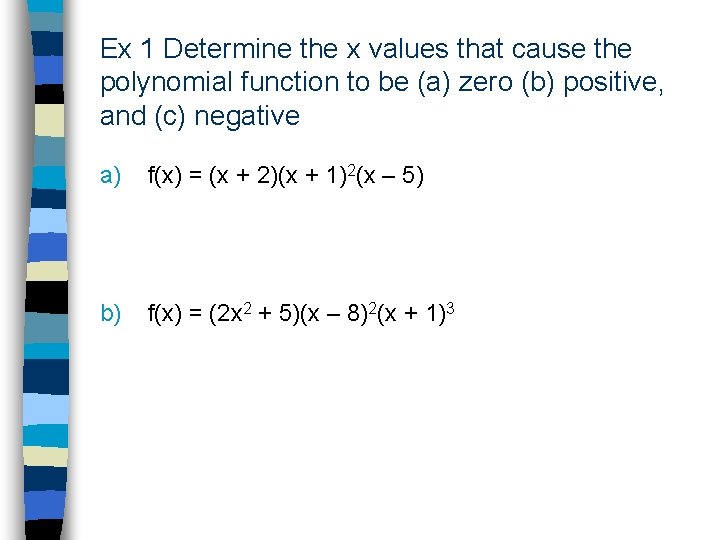
Ex 1 Determine the x values that cause the polynomial function to be (a) zero (b) positive, and (c) negative a) f(x) = (x + 2)(x + 1)2(x – 5) b) f(x) = (2 x 2 + 5)(x – 8)2(x + 1)3

Our work in the previous example allows us to report the solutions of four polynomial inequalities: The solution of f(x) = (x + 2)(x + 1)2(x – 5) > 0 is The solution of f(x) = (x + 2)(x + 1)2(x – 5) ≥ 0 is The solution of f(x) = (x + 2)(x + 1)2(x – 5) < 0 is The solution of f(x) = (x + 2)(x + 1)2(x – 5) ≤ 0 is

Important General Characteristics of poly functions and poly inequalities: • Changes sign at its real zeros of odd multiplicity • Touches the x-axis but does not change sign at its real zeros of even multiplicity • Has no x-intercepts or sign changes at its non -real complex zeros associated with irreducible quadratic factors.

Graphing using a sign chart • • • Complete the exploration on p. 259 You have 12 min. The first 6 min. NO TALKING You may discuss your results with a neighbor Prepare to share your results in 2 min.

Ex 2 Complete the factoring, if needed, and solve the polynomial inequality using a sign chart. Support graphically. a) f(x) = 2 x 3 – 3 x 2 – 11 x + 6 ≤ 0 b) f(x) = (x + 1)(x – 3)(x + 2) > 0
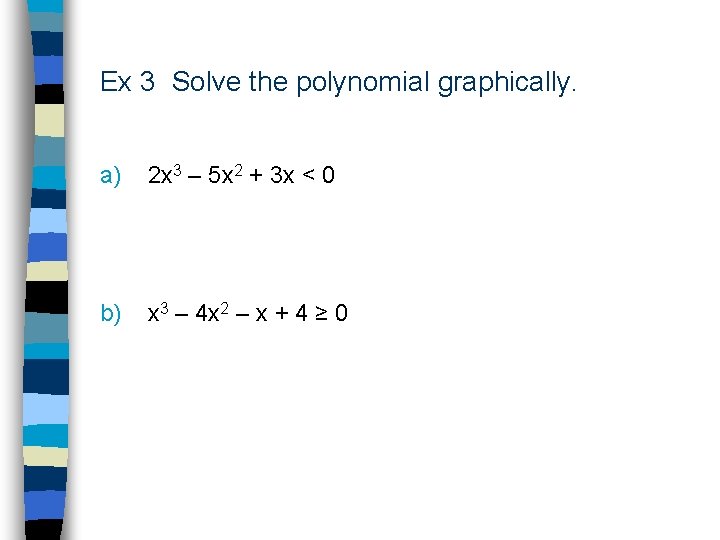
Ex 3 Solve the polynomial graphically. a) 2 x 3 – 5 x 2 + 3 x < 0 b) x 3 – 4 x 2 – x + 4 ≥ 0

Ex 3 Solve the rational inequality using a sign test & support graphically. a) x 2 + 3 x + 2 < 0 x– 1 b) x 3 – 4 x 2 – x + 4 ≥ 0 2 x 2 – 3 x + 1
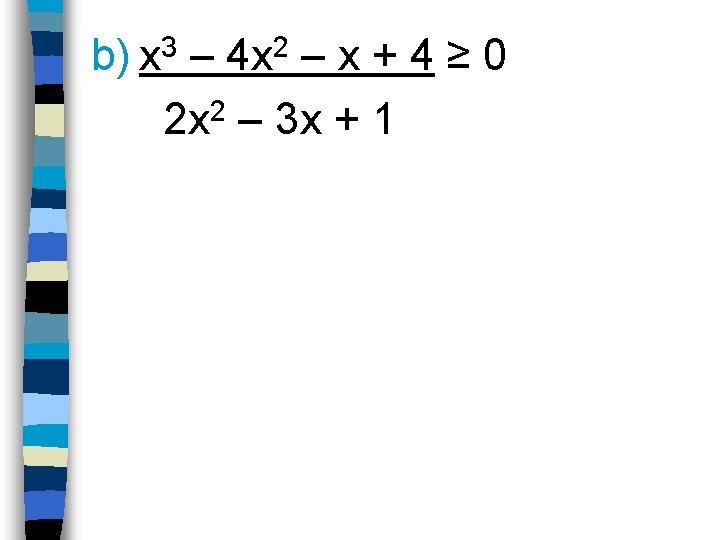
- Slides: 15