2 8 Phase Shifts and Sinusoidal Curve Fitting

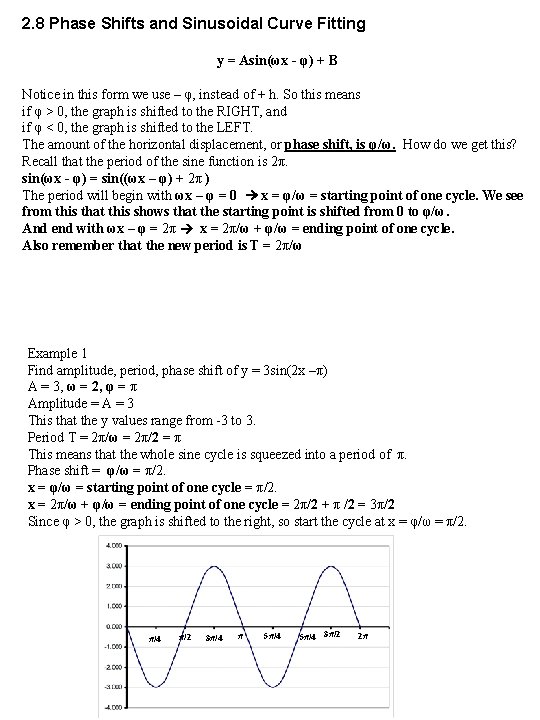
2. 8 Phase Shifts and Sinusoidal Curve Fitting y = Asin(ωx - φ) + B Notice in this form we use – φ, instead of + h. So this means if φ > 0, the graph is shifted to the RIGHT, and if φ < 0, the graph is shifted to the LEFT. The amount of the horizontal displacement, or phase shift, is φ/ω. How do we get this? Recall that the period of the sine function is 2π. sin(ωx - φ) = sin((ωx – φ) + 2π ) The period will begin with ωx – φ = 0 x = φ/ω = starting point of one cycle. We see from this that this shows that the starting point is shifted from 0 to φ/ω. And end with ωx – φ = 2π x = 2π/ω + φ/ω = ending point of one cycle. Also remember that the new period is T = 2π/ω Example 1 Find amplitude, period, phase shift of y = 3 sin(2 x –π) A = 3, ω = 2, φ = π Amplitude = A = 3 This that the y values range from -3 to 3. Period T = 2π/ω = 2π/2 = π This means that the whole sine cycle is squeezed into a period of π. Phase shift = φ/ω = π/2. x = φ/ω = starting point of one cycle = π/2. x = 2π/ω + φ/ω = ending point of one cycle = 2π/2 + π /2 = 3π/2 Since φ > 0, the graph is shifted to the right, so start the cycle at x = φ/ω = π/2. π/4 π/2 3π/4 π 5π/4 3π/2 2π

Example 3 Finding a Sinusoidal Functions from Temperature Data Month Average Monhly Temp 1 29. 7 2 33. 4 3 39 4 48. 2 5 57. 2 6 66. 9 7 73. 5 8 71. 4 9 62. 3 10 51. 4 11 39 12 31 We will fit this to the STANDARD sinusoidal function: y = Asin(ωx - φ) + B Step 1: To find the amplitude A, we compute A= Step 2: Determine the vertical shift, B, by finding the average of the highest and lowest value. B= Step 3: Find frequency, ω. Cycle will (hopefully) repeat itself every year, so period = 12 months. T = 12. Use the fact that T = 2π/ ω to solve for ω. ω = 2π/T = 2π/12 = π/6 Step 4: Using A=21. 9, ω = π/6, and B = 51. 6, determine horizontal shift by choosing an arbitrary data point (x, y) from the given table and solving the equation for φ.

Let’s choose the first data point, x = 1 (Jan. ), y = 29. 7 So. . A sine function that fits the data is

Homework Sec. 2. 8 p. 206 #3 -27 EOO