2 6 Solving Linear Inequalities 1 Represent solutions

2. 6 Solving Linear Inequalities 1. Represent solutions to inequalities graphically and using set notation. 2. Solve linear inequalities.

Inequalities < is less than > is greater than is less than or equal to is greater than or equal to Inequality always points to the smaller number. True or False? 4 4 4>4 True False Represent inequalities: x > 4 is the same as {5, 6, 7…} False Graphically Interval Notation Set-builder Notation

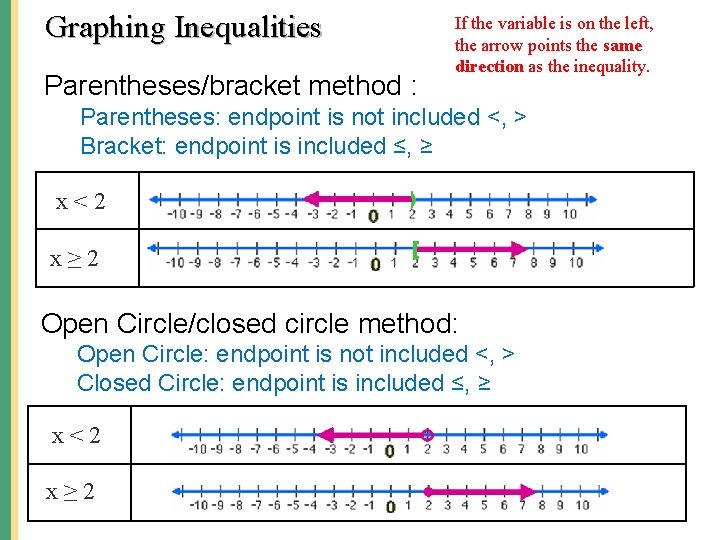
Graphing Inequalities Parentheses/bracket method : If the variable is on the left, the arrow points the same direction as the inequality. Parentheses: endpoint is not included <, > Bracket: endpoint is included ≤, ≥ x<2 x≥ 2 Open Circle/closed circle method: Open Circle: endpoint is not included <, > Closed Circle: endpoint is included ≤, ≥ x<2 x≥ 2

Inequalities – Interval Notation [( smallest, largest )] Parentheses: endpoint is not included <, > Bracket: endpoint is included ≤, ≥ Infinity: always uses a parenthesis x<2 ( –∞, 2) x≥ 2 [2, ∞) 4<x<9 3 -part inequality (4, 9)

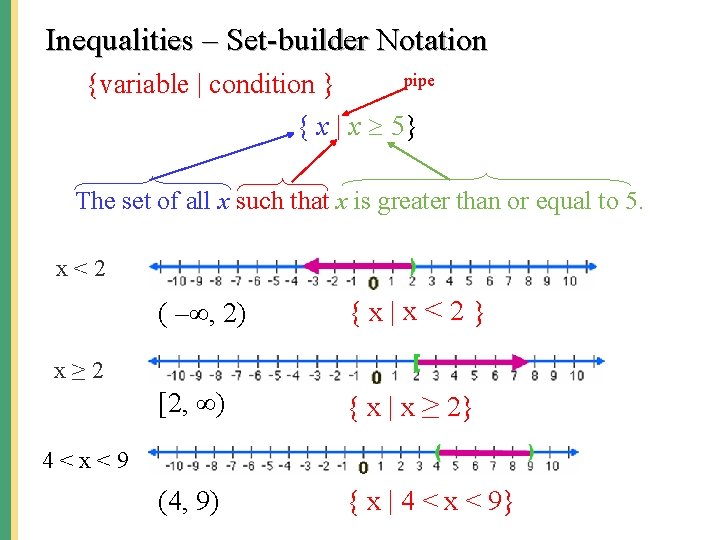
Inequalities – Set-builder Notation {variable | condition } pipe { x | x 5} The set of all x such that x is greater than or equal to 5. x<2 ( –∞, 2) {x|x<2} [2, ∞) { x | x ≥ 2} (4, 9) { x | 4 < x < 9} x≥ 2 4<x<9

Inequalities Graph, then write interval notation and set-builder notation. x≥ 5 [ Interval Notation: [ 5, ∞) Set-builder Notation: { x | x ≥ 5} x < – 3 ) Interval Notation: (– ∞, – 3) Set-builder Notation: { x | x < – 3 }

Inequalities Graph, then write interval notation and set-builder notation. 1<a<6 ( ) Interval Notation: ( 1, 6 ) Set-builder Notation: { a | 1 < a < 6 } – 7 < x ≤ 3 ( ] Interval Notation: (– 7, – 3] Set-builder Notation: { x | – 7 < x ≤ 3 }

Inequalities 4<5 4+1<5+1 4– 1<5– 1 5<6 3<4 True The Addition Principle of Inequality If a < b, then a + c < b + c for all real numbers a, b, and c. Also true for >, , or .

Inequalities 4<5 4 (2) < 5 (2) 8 < 10 True 4<5 4 (– 2) < 5 (– 2) – 8 < – 10 – 8 > – 10 False If we multiply (or divide) by a negative, reverse the direction of the inequality!!!!! The Multiplication Principle of Inequality If a < b, then ac < bc if c is a positive real number. If a < b, then ac > bc if c is a negative real number. The principle also holds true for >, , and .

Solving Inequalities If we multiply (or divide) by a negative, reverse the direction of the inequality!!!!!

Solving Inequalities Solve then graph the solution and write it in interval notation and set-builder notation. Don’t write = ! ( Interval Notation: ( 1, ∞ ) Set-builder Notation: { x | x > 1 }

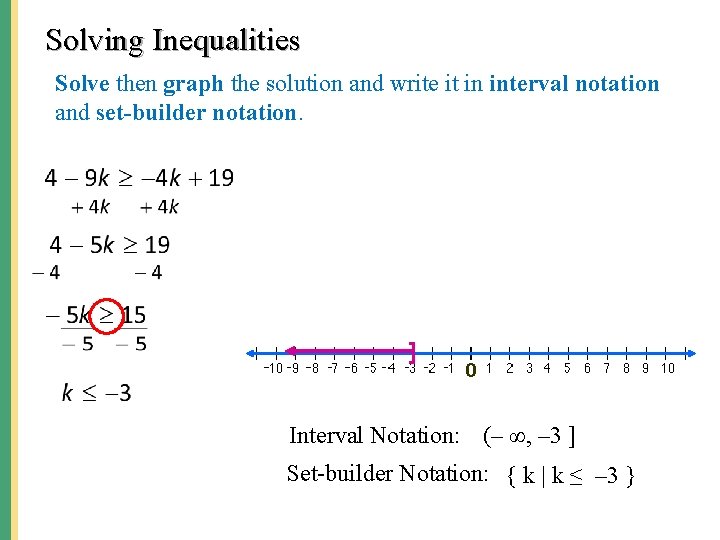
Solving Inequalities Solve then graph the solution and write it in interval notation and set-builder notation. ] Interval Notation: (– ∞, – 3 ] Set-builder Notation: { k | k ≤ – 3 }

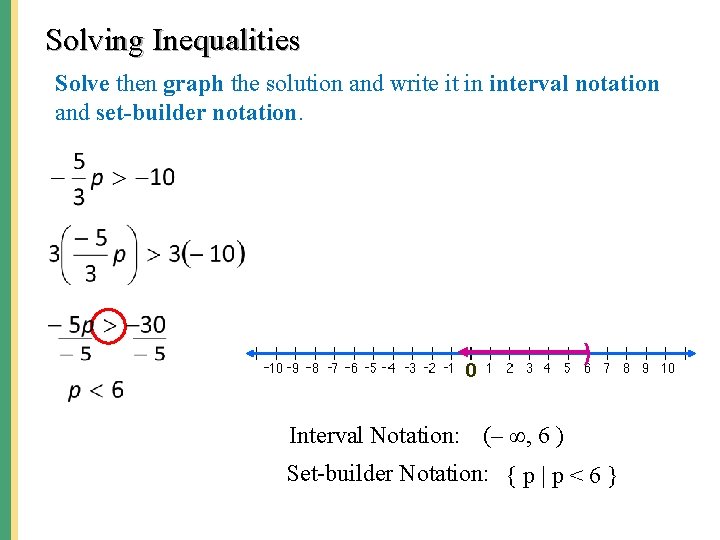
Solving Inequalities Solve then graph the solution and write it in interval notation and set-builder notation. ) Interval Notation: (– ∞, 6 ) Set-builder Notation: { p | p < 6 }

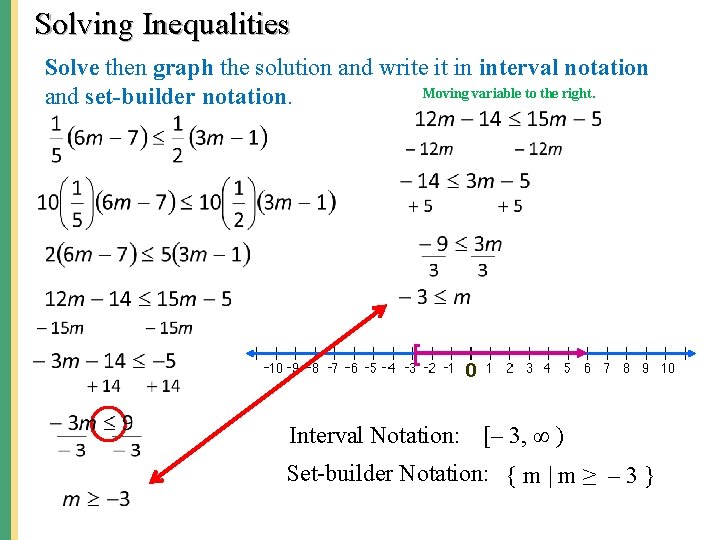
Solving Inequalities Solve then graph the solution and write it in interval notation Moving variable to the right. and set-builder notation. [ Interval Notation: [– 3, ∞ ) Set-builder Notation: { m | m ≥ – 3 }