2 6 BOUNDINGVOLUME HIERARCHIES Overview of different forms

2. 6. BOUNDINGVOLUME HIERARCHIES Overview of different forms of bounding volume hierarchy

BOUNDING VOLUME HIERARCHIES Exploration of different types of bounding volume hierarchy

Bounding Volume Hierarchies Given a total of n objects, a simple brute force approach towards producing a list of intersecting objects is to consider all object pairings (i. e. n 2/2 comparisons). Assuming each object can be described in terms of one of more bounding volumes, by arranging the object’s bounding volumes into a tree-based hierarchy (known as a bounding volume hierarchy), a logarithmic order time complexity can be obtained.

BVH Design Issues: Desirable Characteristics Desirable characteristics of a game-oriented BVH are likely to include: • Pruning a node near the rootgiven of the tree should be spatially ‘close’ The nodes contained in any sub-tree should to eachremove other. more objects from further than removalshould of a deeper • consideration Each node in the hierarchy be of node. minimal volume. • The volume of overlap between sibling nodes should be minimal. • The hierarchy should be balanced with respect to both its node structure and its content. • The worst-case time for queries should not be much worse than the average-case query time. Aside: BVH d spatial partit iffer from schemes (exp ioning lecture) in thlored next volumes can at two BVH same space cover the and objects typically only are f o u n d in single volum a e. S p a t ia l partitioning s c h e m e s typically req overlapping uire nonpermit objecregions but two or morets to be in partitions.

number of objects increase it is not possible to use an exhaustive (optimal) search. Instead, heuristic rules are used to direct the BVH construction (selecting the best option from a small number of hopefully near optimal options at each step). BVH Building Strategies There are three main categories of tree construction methods: • top-down • bottom-up • insertion

to implement and hence popular). • Bottom-up: start with leaves of the tree, group two (or more) to form a bounding node, progressively grouping bounded volumes until a single node is reached (typically produces best quality BVH, but more difficult to implement). BVH Building Strategies • Insertion: incrementally insert an object into the tree so as to minimize some insertion cost measurement Top-down a bottom-up nd line methodare offrequire all ps as they to be availabrimitives before const le starts. Inser ruction construction considered o is as it can be n-line game run-t used at ime.

Consult the recommended course text for full details of the following approaches: • Top-downof Construction Forms BVH Construction • Bottom-up Construction • Incremental (Insertion) Construction Top-down construction is explored next by way of an example.

TOP -DOWN CONSTRUCTION Top-down construction of a bounding volume hierarchy

Top-down Construction of a BVH The process of top-down construction can be algorithmically described as: void Build. Top. Down. BVH(BVHNode tree. Node, Array. List objects) { Node new. Node = new Node(); Create an empty node and add to the tree. Node. add(new. Node); Build a suitable bounding volume around the specified object list new. Node. Bounding. Volume = Compute. Bounding. Volume(objects); if( objects. Count <= MIN_OBJECTS_PER_LEAF ) { If needed, new. Node. Type = LEAF; simply store the new. Node. Objects = objects; object list within } else { this node new. Node. Type = NODE; Sort and split the objects into two int split. Idx = Rearrange. And. Partition. Objects(objects); partitions Build. Top. Down. BVH( Recursively build the BVH along the defined left and new. Node. Left. Tree, objects. Subset(0, split. Idx)); right sub-trees Build. Top. Down. BVH( new. Node. Right. Tree, objects. Subset(split. Idx, objects. Count); } }

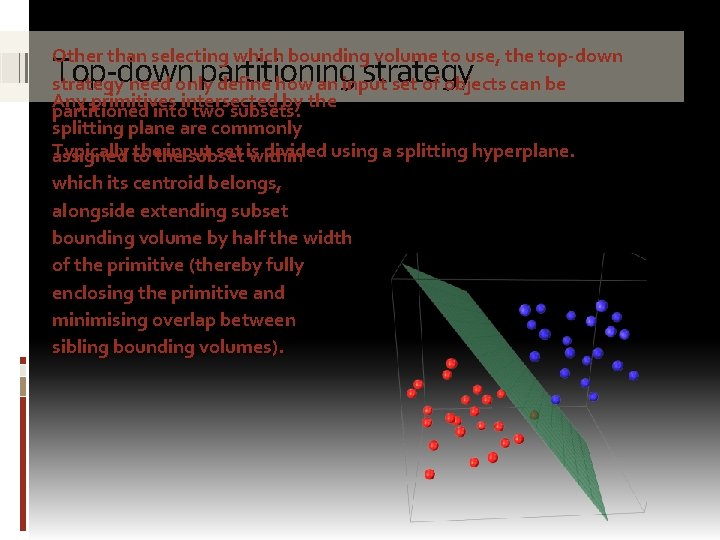
Other than selecting which bounding volume to use, the top-down strategy need only define how an input set of objects can be Any primitives by the partitioned intointersected two subsets. splitting plane are commonly Typically to thethe input set is divided using a splitting hyperplane. assigned subset within which its centroid belongs, alongside extending subset bounding volume by half the width of the primitive (thereby fully enclosing the primitive and minimising overlap between sibling bounding volumes). Top-down partitioning strategy

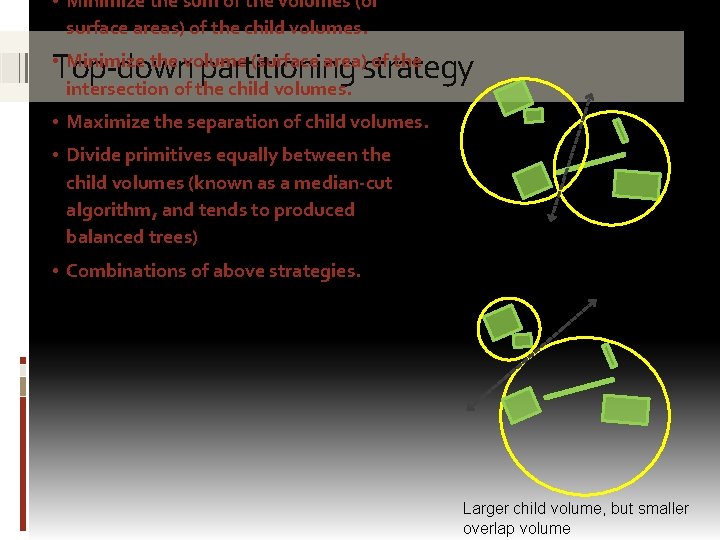
• Minimize the sum of the volumes (or surface areas) of the child volumes. Top-down partitioning strategy • Minimize the volume (surface area) of the intersection of the child volumes. • Maximize the separation of child volumes. • Divide primitives equally between the child volumes (known as a median-cut algorithm, and tends to produced balanced trees) • Combinations of above strategies. Assuming spherical bounding volumes Minimal child volume, but high overlap volume Larger child volume, but smaller overlap volume

• The volume of the bounding volume falls below a cut-off limit. • The depth of the node has reached a predefined cut-off depth. Top-down partitioning: Halting recursion Partitioning might also fail because: • All primitives fall on one side of the split plane. • One or both child volumes end up with as many (or nearly as many) primitives as the parent volume. • Both child volumes are (almost) as large as the parent volume. In these cases, it is reasonable to try other partitioning criteria before terminating the recursion.

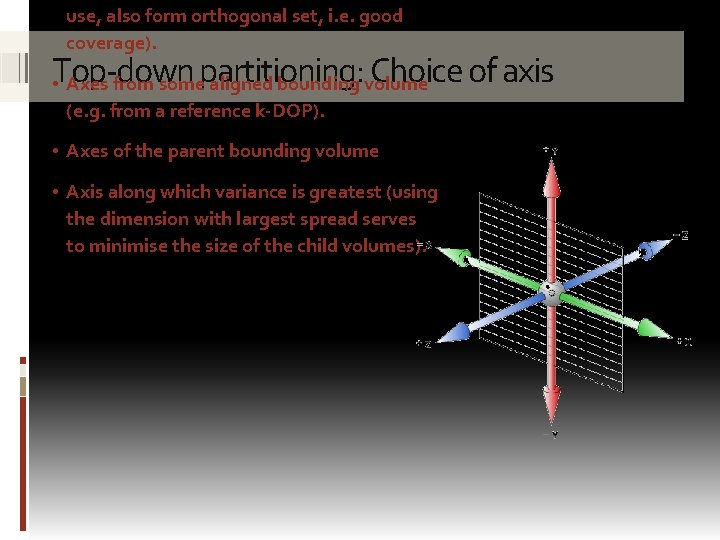
use, also form orthogonal set, i. e. good coverage). Top-down partitioning: Choice of axis • Axes from some aligned bounding volume (e. g. from a reference k-DOP). • Axes of the parent bounding volume • Axis along which variance is greatest (using the dimension with largest spread serves to minimise the size of the child volumes).

Top-down partitioning: Choice of split point • The Object median: splitting • Object mean: choice of which split point to use is at the middle object to the following: splitting at the (also) often restricted (thereby evenly mean object offset distributing the primitives (e. g. along the axis and providing a balanced with greatest tree). variance). • Bounding volume median: splitting at the middle of the bounding volume (thereby splitting into two equal parts). (a) Splits at object median, (b) splits at object mean, (c) splits at spatial median

HIERARCHY TRAVERSAL Approaches to traversing bounding volumes hierarchies

Approaches include breadth-first (BFS) and depthfirst (DFS) searches. BFS explores all nodes at a given depth before descending. DFS descends down into the tree, backtracking up once a leaf is hit. Hierarchy Traversal A decent method is blind (or uninformed) if it only uses the tree structure to select the next node. Informed methods examine node data (e. g. using heuristics) to select the next node (e. g. a best-first search maintains a list of best-scoring moves). For collision detection systems, DFS (possibly a simple heuristic – i. e. basically a best-first approach) is typically favoured over BFS.

Descent Rules Given two BVHs the following descent strategies might be adopted: 1. Descend A before B (or vice versa). Fully descend into the leaves of A before starting to descend into B. This will be very expensive if B’s root bound fully contains A and/or if A contains lots of nodes. 2. Descend the larger volume. Dynamically determine which BVH node is currently larger and descend into (avoiding the problems of Approach 1). 3. Descend A and B simultaneously. Similar to Approach 2 but without any cost evaluation f Which type o ost overhead (but it may not prune space as traversal is m s ective depend ff e efficiently). e entirely on th 4. Descend based on overlap. Similar to Approach 2, priortise descent on degree of overlap between BVH regions. he structure of t data, as the indicated bymple. refinery exa

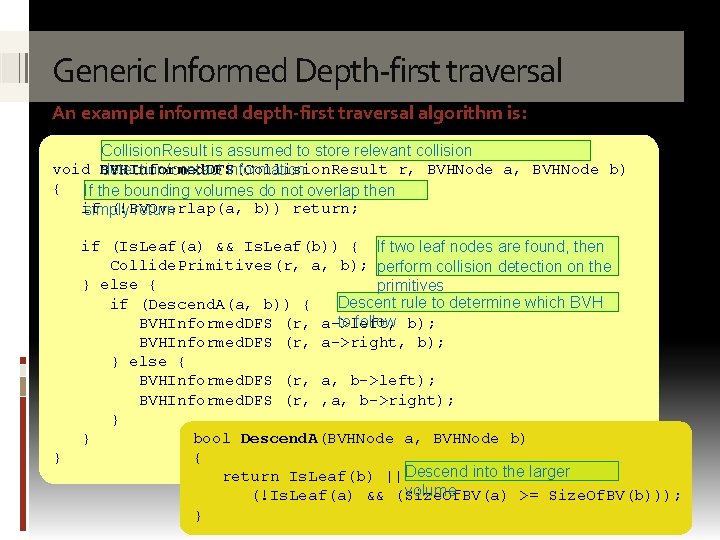
Generic Informed Depth-first traversal An example informed depth-first traversal algorithm is: Collision. Result is assumed to store relevant collision void BVHInformed. DFS(Collision. Result r, BVHNode a, BVHNode b) detection/contact information { If the bounding volumes do not overlap then if (!BVOverlap(a, b)) return; simply return } if (Is. Leaf(a) && Is. Leaf(b)) { If two leaf nodes are found, then Collide. Primitives(r, a, b); perform collision detection on the } else { primitives Descent rule to determine which BVH if (Descend. A(a, b)) { to follow b); BVHInformed. DFS (r, a->left, BVHInformed. DFS (r, a->right, b); } else { BVHInformed. DFS (r, a, b->left); BVHInformed. DFS (r, , a, b->right); } bool Descend. A(BVHNode a, BVHNode b) } { return Is. Leaf(b) || Descend into the larger volume (!Is. Leaf(a) && (Size. Of. BV(a) >= Size. Of. BV(b))); }

Descent Rules See the source text book for: • A non-recursive, faster, implementation of the generic informed depth-first traversal • Simultaneous depth-first traversal algorithm • Optimised leaf-directed depth-first traversal

ed ect r i g D din a e r DIRECTED READING Directed mathematical reading

Directed reading • Read Chapter 6 of Real Time Collision Detection (pp 235 -284) ed ect r i g D din rea • Related papers can be found from: http: //realtimecollisiondetection. net/books/rtcd/references/

Summary Today we explored: ü Bounding volume hierarchies ü Overview of top-down construction approaches : o d o T cted e r i d e h t d a e üR material he t g n i d a e r r e üAft ave h , l a i r e t a m directed is the s i h t f i r e d n a po you l a i r e t a m f o type ore l p x e o t e k i l would t. c e j o r p a n i h t wi