2 5 Using Linear Models Make predictions by

2 -5 Using Linear Models Make predictions by writing linear equations that model real-world data.

Scatter Plots • A scatter plot is a graph that displays two sets of data as ordered pairs. • Scatter plots can help show whether or not two sets of data are related.

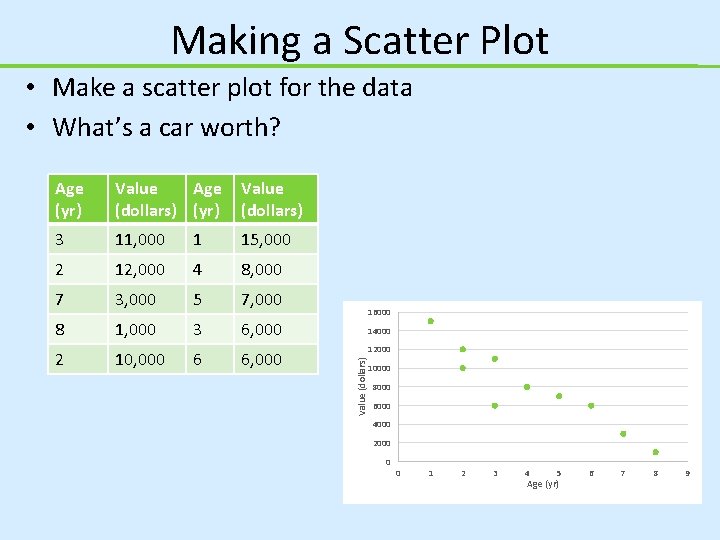
Making a Scatter Plot • Make a scatter plot for the data • What’s a car worth? Value Age (dollars) (yr) Value (dollars) 3 11, 000 1 15, 000 2 12, 000 4 8, 000 7 3, 000 5 7, 000 8 1, 000 3 6, 000 2 10, 000 6 6, 000 16000 14000 12000 Value (dollars) Age (yr) 10000 8000 6000 4000 2000 0 0 1 2 3 4 5 Age (yr) 6 7 8 9

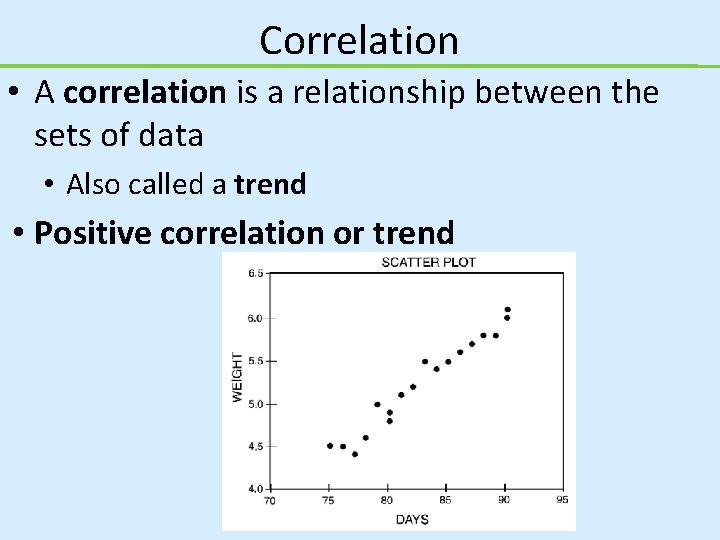
Correlation • A correlation is a relationship between the sets of data • Also called a trend • Positive correlation or trend

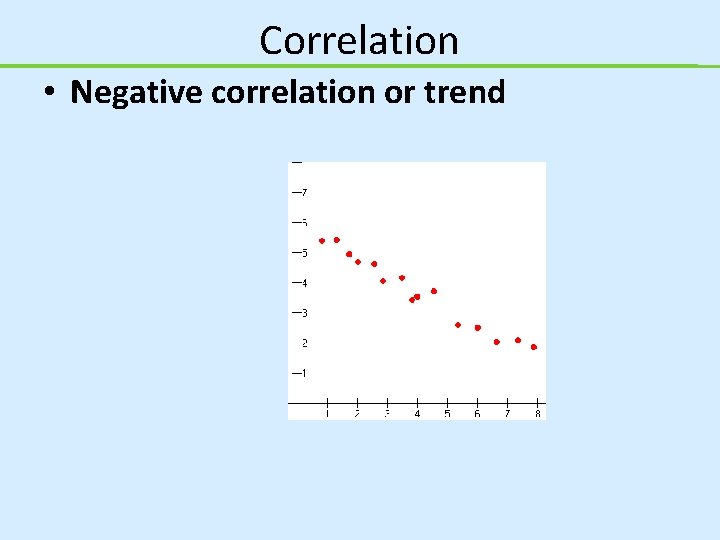
Correlation • Negative correlation or trend

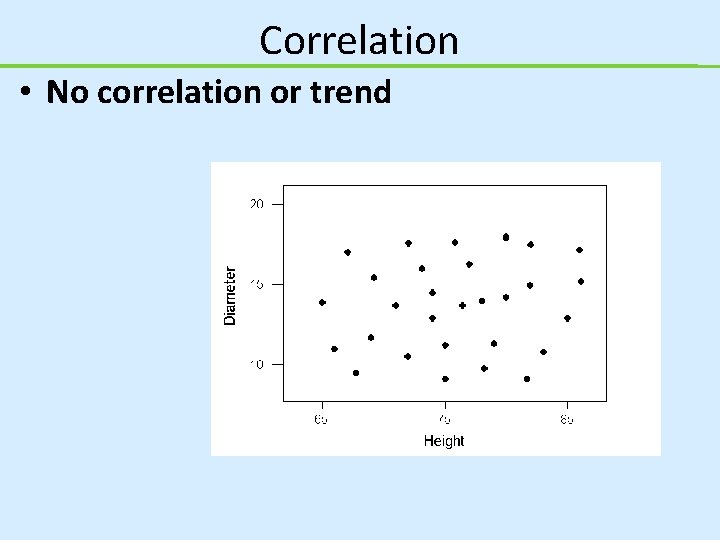
Correlation • No correlation or trend

Line of Best Fit • A line you draw on a graph to approximate the relationship between data sets. • Also called a trend line • A line of best fit should have an equal number of data points on each side • If there is no correlation, you cannot draw a line of best fit

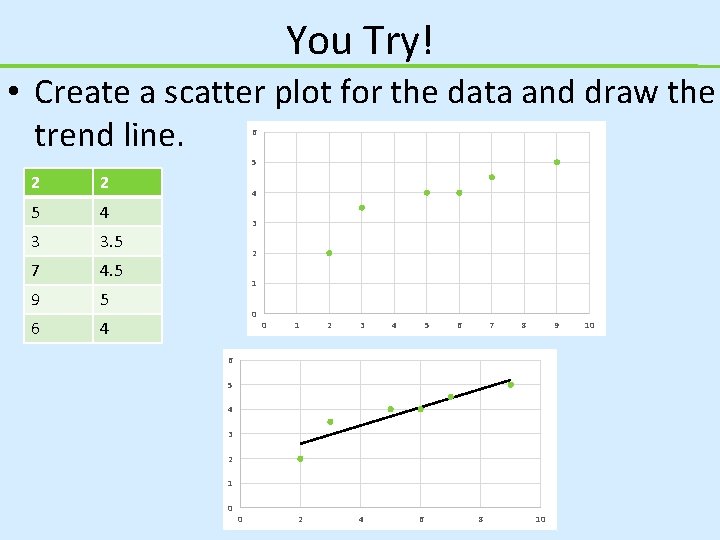
You Try! • Create a scatter plot for the data and draw the trend line. 6 5 2 2 5 4 3 3. 5 7 4. 5 9 5 6 4 4 3 2 1 0 0 1 2 3 4 5 6 7 8 9 6 5 4 3 2 1 0 0 2 4 6 8 10 10

Making Predictions • What is the approximate weight of a 7 month old panda? • We have just used interpolation to estimate a value between two known values using a line of best fit. • Extrapolation is used to predict a value outside the range of known values. • Ex: Use your model to find the body weight of a 3 -year old panda.

Causation • A change in one quantity causes a change in the second quantity. • Correlation does not always imply causation

Using a Calculator • Correlation coefficient (r) can be found using a graphing calculator. – Ranges between -1 and 1 – The nearer r is to 1 or -1, the more closely the trend line fits the data – r close to 1 shows a strong positive correlation – r close to -1 shows a strong negative correlation – r close to 0 means a weaker correlation or no correlation

Using a Calculator • Press STAT and then 1 to select EDIT • Enter x-values into L 1 and y-values into L 2 – (if x-values are years, do not enter the year, but enter 1 for one year from the start, 2 for 2 years from start, etc. ) • Press STAT then move Right to the CALC menu • Move Down to Lin. Reg(ax+b) and press Enter • Press Enter again – a will represent slope – b will represent the y-intercept – And r will show the correlation coefficient (NOT r 2)

Assignment • ODDS • P. 96 #7 -17