2 5 Reason Using Properties from Algebra Objective

2. 5 Reason Using Properties from Algebra Objective: To use algebraic properties in logical arguments.

Algebraic Properties • Addition Property: If a = b, then a + c = b + c. • Subtraction Property: If a = b, then a – c = b – c. • Multiplication Property: If a = b, then ac = bc. • Division Property: If a = b and c = 0, then a/c = b/c.

Algebraic Properties • Substitution Property: If a = b, then a can be substituted for b in an equation or expression. • Distributive Property: a(b + c) = ab + ac, where a, b, and c are real numbers.

Example 1: Write a two-column proof to solve the equation. 3 x + 2 = 8 Statements Reasons 1. 2. 3. 4. 5. Given 3 x + 2 = 8 3 x + 2 – 2 = 8 – 2 3 x = 6 3 x ÷ 3 = 6 ÷ 3 x=2 Subtraction Prop Simplify Division Prop Simplify

Example 2: Write a two-column proof to solve the equation. Statements Reasons 1. 2. 3. 4. 5. 6. Given 4 x + 9 = 16 – 3 x 4 x + 9 + 3 x = 16 – 3 x + 3 x 7 x + 9 = 16 7 x + 9 – 9 = 16 – 9 7 x = 7 7 x ÷ 7 = 7 ÷ 7 7. x = 1 Addition Prop Simplify Subtraction Prop Simplify Division Prop Simplify

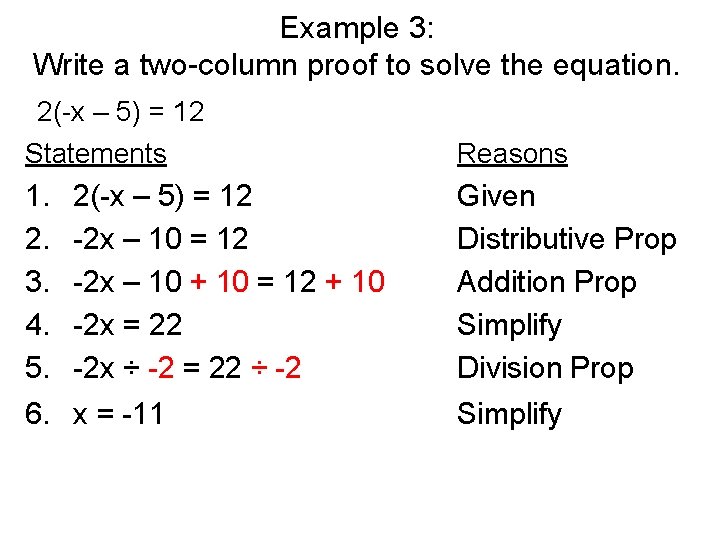
Example 3: Write a two-column proof to solve the equation. 2(-x – 5) = 12 Statements Reasons 1. 2. 3. 4. 5. 6. 2(-x – 5) = 12 -2 x – 10 + 10 = 12 + 10 -2 x = 22 -2 x ÷ -2 = 22 ÷ -2 Given Distributive Prop Addition Prop Simplify Division Prop x = -11 Simplify

Algebraic Properties • Reflexive Property: For any real number a, a = a For any segment AB, AB = AB For any angle A, m<A = m<A • Symmetric Property: For any real numbers a and b, if a = b, then b = a For any segments AB and CD, if AB = CD, then CD = AB For any angles A and B, if m<A = m<B, then m<B = m<A

Algebraic Properties (cont) Transitive Property: For any real numbers a, b and c, if a = b and b = c, then a = c. For any segments AB, CD, and EF, if AB = CD and CD = EF, then AB = EF. For any angles A, B and C, if m<A = m<B, and m<B = m<C then m<A = m<C

Example 4 In the diagram, AB = CD. Show that AC = BD. Statement AB = CD Reason Given AC = AB + BC Segment Addition Postulate BD = BC + CD Segment Addition Postulate AB + BC = CD + BC AC = BD Addition Property of Equality Substitution Property of Equality

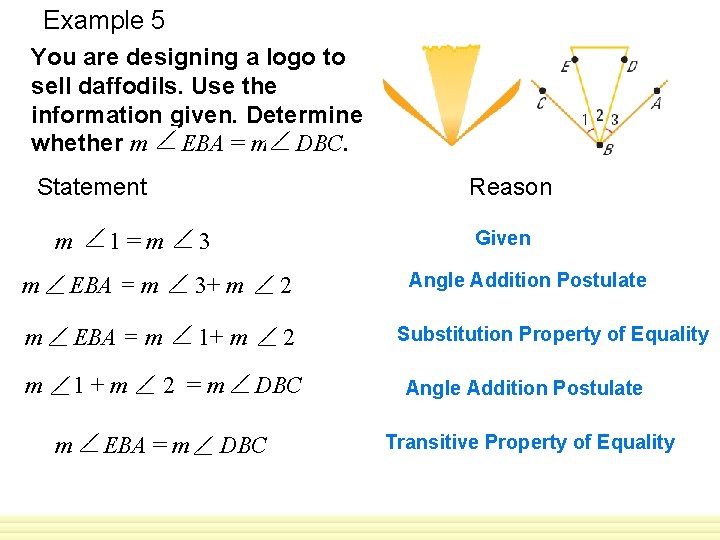
Example 5 You are designing a logo to sell daffodils. Use the information given. Determine whether m EBA = m DBC. Statement m Reason 1=m Given 3 m EBA = m 3+ m 2 m EBA = m 1+ m 2 m 1+m m 2 =m EBA = m DBC Angle Addition Postulate Substitution Property of Equality Angle Addition Postulate Transitive Property of Equality

Example 5: 6 Example Name the property of equality the statement illustrates. a). If m 6=m 7, then m 7=m 6. ANSWER Symmetric Property of Equality b). If JK = KL and KL = 12, then JK = 12. ANSWER Transitive Property of Equality

Example 5 cont’d: c). m W=m W ANSWER Reflexive Property of Equality d). If L = M and M = 6, then L = 6 ANSWER Transitive Property of Equality