2 5 Problem Solving Essential Question 1 How

2. 5 Problem Solving Essential Question: 1) How do you create an equation for applications?

Problem-Solving • Today we are going to work on problemsolving by creating equations for geometry, integer, and distance applications. • To create an equation: – Define the variable(s) – Use known formulas – Substitute in values based on known values and variables

Geometry Applications • You need to recall basic geometry formulas such as area and perimeter for basic shapes. • What is the formula for perimeter of a rectangle? • The formula for perimeter of a rectangle is P=2 l + 2 w where l is length and w is width.

Example 1 The length of a rectangle is 6 inches more than its width. The perimeter is 24 inches. What is the length of the rectangle? 1) Define 2) Write 3) Solve

Practice 1 The width of a rectangle is 2 cm less than its length. The perimeter is 16 cm. What is the length of the rectangle? 1) Define 2) Write 3) Solve

Consecutive Integers • Consecutive means in sequence or counting by 1. – Example: 50 and 51 are consecutive integers. – 40 and 42 are consecutive even integers. – 35 and 37 are consecutive odd integers. • What is another example?

Example 2 • The sum of three consecutive integers is 147. Find the integers. 1) Define 2) Write 3) Solve

Practice 2 • The sum of three consecutive integers is 48. Find the integers. 1) Define 2) Write 3) Solve

Practice 2 a • How would this change if we used odd numbers? • The sum of two consecutive odd integers is 48. Find the integers. 1) Define 2) Write 3) Solve

Summary • Answer the essential question in complete sentences. • 1) How do you create an equation for applications? • Write 1 -3 study questions for the left column.

2. 5 Problem Solving Essential Question: 2) How do you setup travel applications?

TRAVEL PROBLEMS • Need the formula Distance = rate ∙ time or D=r∙t • Use a table to set up and balance the equation. • THE EQUATION NEEDS TO BE BALANCED BY RATE. Object or Rate Direction traveling #1 #2 Time DISTANCE

Example 3: Same-Direction • Same-Direction means they are going the same distance, so they are equal.
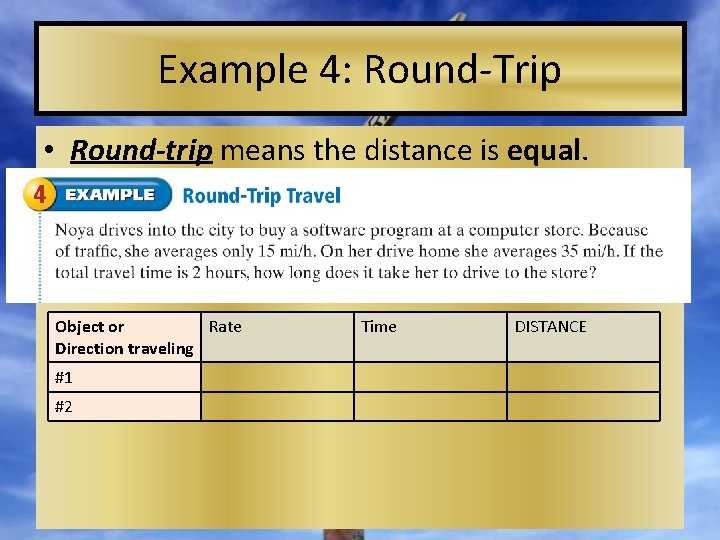
Example 4: Round-Trip • Round-trip means the distance is equal. Object or Rate Direction traveling #1 #2 Time DISTANCE

Example 5: Opposite Direction • Opposite directions means the sum of the distances equals the total distance apart. Object or Rate Direction traveling #1 #2 Time DISTANCE

Summary • Answer the essential question in complete sentences. • 2) How do you setup travel applications? • Write 1 -3 study questions for the left column.
- Slides: 16