2 5 Multiplication of Real Numbers 2 5

2. 5. Multiplication of Real Numbers

2. 5 Multiplication of Real Numbers • Good news! The rules for multiplying are easier to remember than the rules for adding… Factor 1 Factor 2 Product + + + – – – + –

Let’s Try It Out Examples: Find the Product. • (-3)(2) = • (4)(-2) = • (-7)(-6) = • (8)(9)=

Example 1: More Than Two Numbers How do you multiply when you have more than two numbers with various signs? Let’s try a few: • (-3)(4)(-2) = • (-4)(-3)(-5)= • (-1)4 =

Example 1: More Than Two Numbers Is (-1)4 the same as -14 ? • (-1)4 = (-1)(-1) • -14 = -(1 • 1 • 1) • So, (-1)4 = +1 and -14 = -1 • No, Not the Same!

Example 1: More Than Two Numbers • Do you notice a pattern? • (-1) = • (-1)(-1)(-1)(-1) = • (-1)(-1)(-1) =

Pattern Rule – If you have an even number of negative factors, you get a positive result – If you have an odd number of negative factors, you get a negative result

Simplify the Variable Expression • (5)(-x) • (-3)(z)2(z) • (-y)2(y)2

Evaluate the Expression • x 3 + 2 when x = -2 • 2 x 2 - 3 x + 1 when x = 2

Complete the Statement using = or ≠ • 5(-4) ___ (-4)(5) • (5 x)(5 x) ___ 3(5 x)

2. 6. The Distributive Property

Distributive Property The product of a and (b + c) follows this rule: a (b + c) = ab + ac Example: 4(3 + 2) = 4(3) + 4(2) = 12 + 8 = 20

Distributive Property Another Example: 5(x + 6) = 5 x + 5(6) = 5 x + 30

Distributive Property What about (b + c)a ? The easiest way to deal with this is to use the commutative property (b + c)a = a(b + c)

Distributive Property What about a(b – c) ? Subtraction is just addition of the opposite: a(b – c) = a(b + -c) = ab + -ac = ab – ac
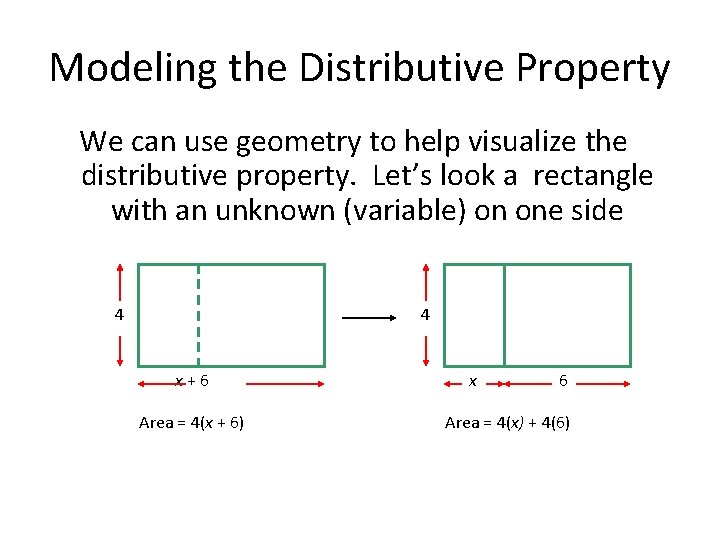
Modeling the Distributive Property We can use geometry to help visualize the distributive property. Let’s look a rectangle with an unknown (variable) on one side 4 4 x+6 Area = 4(x + 6) x 6 Area = 4(x) + 4(6)

Using the Distributive Property 2(x + 5) (x – 4)x (1 + 2 x)8 y(1 - y)

Using the Distributive Property 2(x + 5) = 2 x + 10 (x – 4)x = x 2 - 4 x (1 + 2 x)8 = 8 + 16 x y(1 - y) = y - y 2

Using the Distributive Property -3(x + 4) (y + 5)(-4) - (6 x – 3 x) (x-1)(-9 x)

Using the Distributive Property -3(x + 4) = -3 x - 12 (y + 5)(-4) = -4 y - 20 - (6 – 3 x) = -6 + 3 x (x-1)(-9 x) = -9 x 2 + 9 x

Mental Math Calculations You are shopping for t-shirts. You want to buy six t-shirts for $11. 95 each. Use the distributive property to calculate the total cost mentally. Think of $11. 95 as $12. 00 - $0. 05.

Mental Math Calculations The total cost of 6 t-shirts at $11. 95 each is $70.

Simplifying By Combining Like Terms In a term that is the product of a number and variable, the number is the coefficient of the variable. -x + 3 y 2 -1 is the coefficient of x 3 is the of coefficient

Simplifying by Combining Like Terms Like terms are terms in an expression that have the same variable raised to the same power. Example: 5 x and -3 x are like terms. Example: -y + 3 y 2 are not like terms

Using the Distributive Property to Simplify a Function An expression is simplified if it has no grouping symbols and if all the like terms have been combined.

Simplifying by Combining Like Terms 8 x + 3 x = 4 x 2 + 2 – x 2 = 3 – 2(4 + x) =
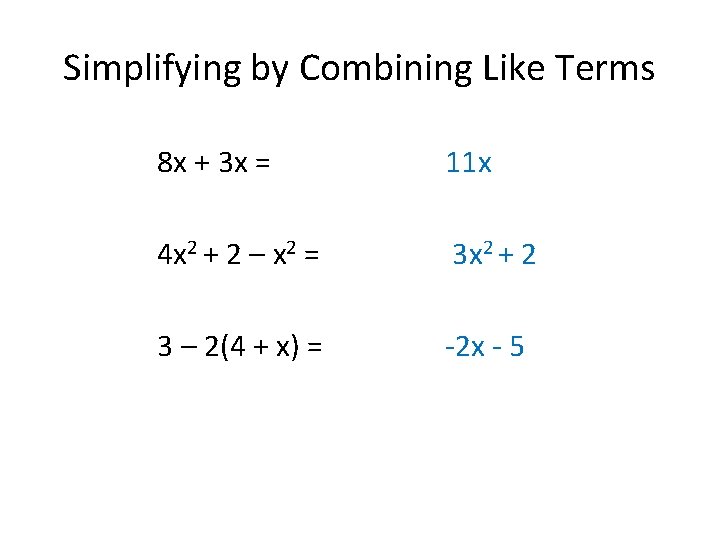
Simplifying by Combining Like Terms 8 x + 3 x = 11 x 4 x 2 + 2 – x 2 = 3 x 2 + 2 3 – 2(4 + x) = -2 x - 5
- Slides: 27