2 5 BASIC PRIMITIVEINTERSECTION Details of common forms

2. 5. BASIC PRIMITIVEINTERSECTION Details of common forms of primitive intersection test

Basic Primitive Intersection Tests Testing if two primitives intersect is often easier (and faster) than determining how two primitives intersect (e. g. generating contact information such as the distance of interpenetration, etc. ).

• Box against plane • Cone against plane • Sphere against AABB • Sphere against OBB • Sphere against triangle • Sphere against polygon • AABB against polygon • Triangle against triangle Types of basic primitive test Two illustrative forms of closest point test are explored next.

SEPARATING AXES Overview of the separating axis theory

The separating-axis test provides a core tool for implementing a range of intersection tests. Separating-axis test The test is based on the separating hyperplane theorem, which states that given two convex sets A and B, either the two sets are intersecting or there exists a separating hyperplane P such that A is on one side of P and B is on the other. The theory is intuitive as two convex objects cannot “curve” around each other. Thus, when they are not intersecting there will be a gap between them into which a plane can be inserted to separate the two objects.

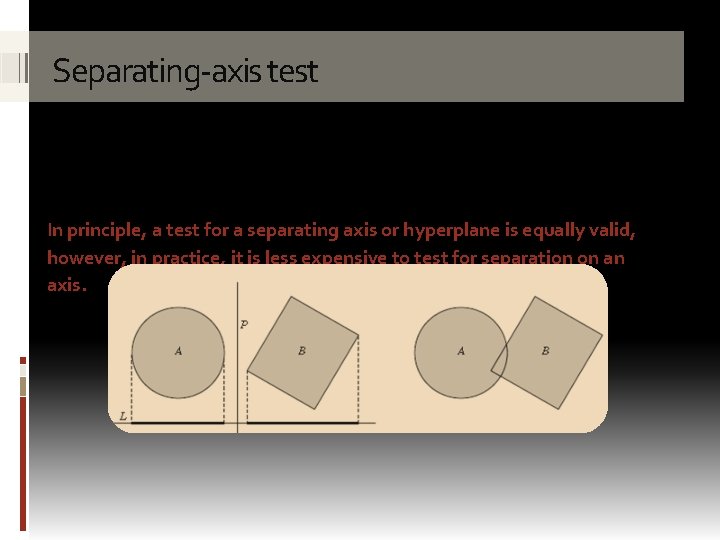
Separating-axis test In principle, a test for a separating axis or hyperplane is equally valid, however, in practice, it is less expensive to test for separation on an axis.

An efficient separation test of two symmetrical objects A and For symmetrical primitives with a defined centre point (e. g. AABBs, B is to compute the halfwidth, OBBs, spheres, etc. ), the centre point will always project onto the or radii, of their projection middle of the projection interval along the tested axis. intervals and compare the sum of them against the distance between their centre projections. Separating-axis test: Symmetrical primitives If the sum is less than the distance between the centre projections, the objects must be disjoint.

For face-face and face-edge cases, the face normals of both objects should be tested as potential separating axes. For edge-edge case, the cross product of the two edges should be tested as the potential separating axis (the points on the edges closest to each other form the feet of a perpendicular between the two edges). Separating-axis test: Arbitrary primitives In summary, to determine intersection of two polyhedral objects, the following axes should be tested for separation: • Axes parallel to face normals of object A • Axes parallel to face normals of object B • Axes parallel to the vectors resulting from the cross products of all edges in A with all edges in B Aside: More fully: this list also includes face-vertex, edgevertex and vertex-vertex, however, the vertex combinations can be considered a special case of edge contact.

As soon as a separating axis is found, a test can exit immediately, i. e. it is not until all identified axes have been tested with no separating axis that the objects must be intersecting. Separating-axis test: Arbitrary primitives Aside: The separating-axis test can also be used to derive contact information, e. g. instead of exiting early when an overlap is detected, all axes are tested for overlap. After all axes have been tested, the axis with the least (normalized) overlap can be used as the contact normal, and the overlap can be used to estimate the penetration depth. With some extra work, contact points can also be computed with the help of the separating axis.

SAMPLE PLANE INTERSECTIONTESTS Sphere and box plane-intersection tests

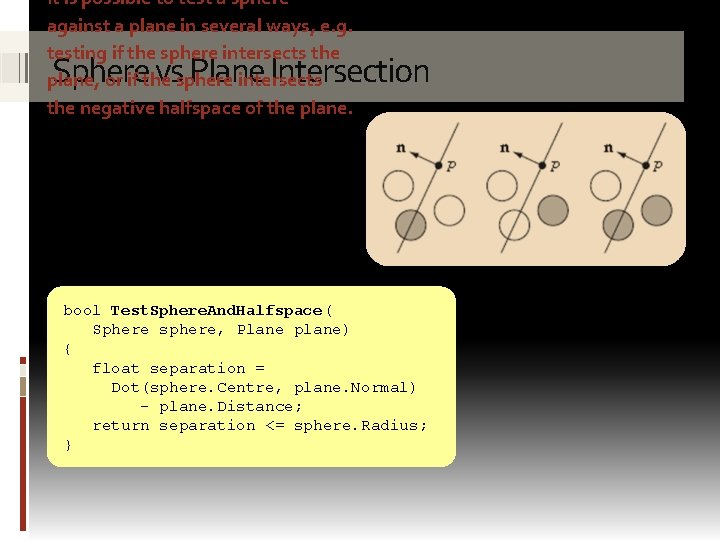
It is possible to test a sphere against a plane in several ways, e. g. testing if the sphere intersects the plane, or if the sphere intersects the negative halfspace of the plane. Sphere vs Plane Intersection bool Test. Sphere. And. Halfspace( Sphere sphere, Plane plane) { float separation = Dot(sphere. Centre, plane. Normal) - plane. Distance; return separation <= sphere. Radius; }

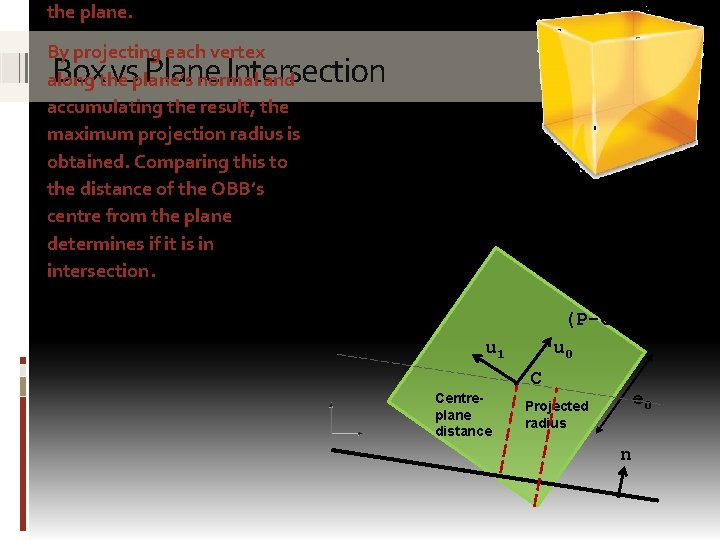
the plane. By projecting each vertex along the plane’s normal and accumulating the result, the maximum projection radius is obtained. Comparing this to the distance of the OBB’s centre from the plane determines if it is in intersection. Box vs Plane Intersection e 1 (P-C)● uo u 0 u 1 ● Centreplane distance C e 0 Projected radius n ●

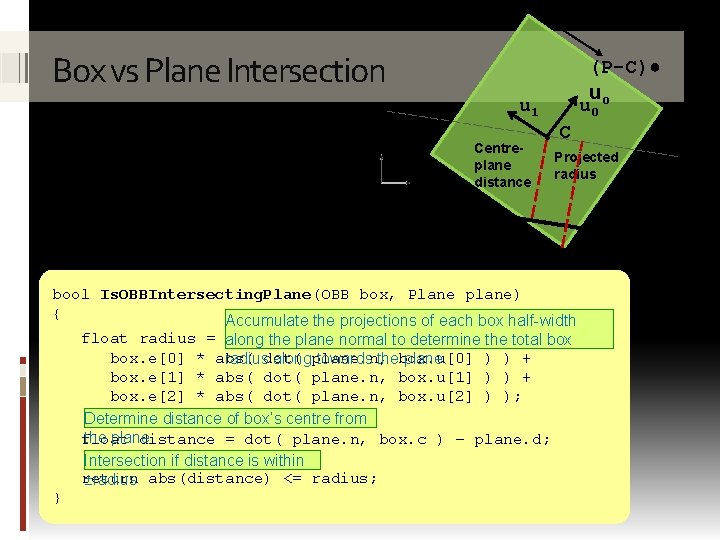
e 1 Box vs Plane Intersection (P-C)● u u 0 o u 1 Centreplane distance ● C e 0 Projected radius n ● bool Is. OBBIntersecting. Plane(OBB box, Plane plane) { Accumulate the projections of each box half-width float radius = along the plane normal to determine the total box. e[0] * abs( ) ) + radiusdot( alongplane. n, towards thebox. u[0] plane. box. e[1] * abs( dot( plane. n, box. u[1] ) ) + box. e[2] * abs( dot( plane. n, box. u[2] ) ); Determine distance of box’s centre from the plane float distance = dot( plane. n, box. c ) – plane. d; Intersection if distance is within return ±radius abs(distance) <= radius; }

RAY INTERSECTIONTESTS Intersection tests involving rays

• Intersecting ray or segment against sphere • Intersecting ray or segment against box • Intersecting line against triangle • Intersecting line against quadrilateral • Intersecting ray or segment against triangle • Intersecting ray or segment against convex polyhedron Intersecting lines rays and segments An illustrative form of ray test is explored next.

Rearranging the above provides a quadratic expression in terms of t, i. e. : Ray or Segment vs. Sphere Solving for t will enable the points of intersection to be determined, i. e. t = -b±√(b 2 -c) where b=m●d and c=(m●m)-r 2 Zero, one or two solutions will be found, negative solutions should be ignored! (P+td-C)●(P+td-C)=r 2 t 2 + 2(m●d)t+(m●m)-r 2 = 0, where m=P-C

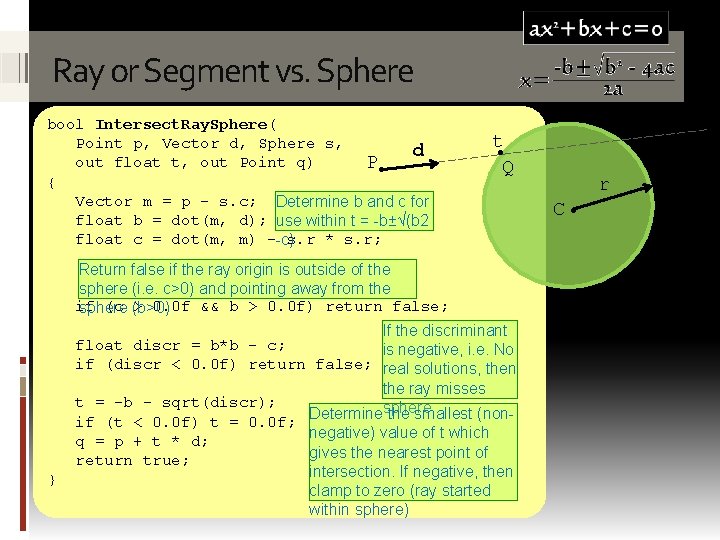
Ray or Segment vs. Sphere bool Intersect. Ray. Sphere( Point p, Vector d, Sphere s, d out float t, out Point q) P● { Vector m = p - s. c; Determine b and c for float b = dot(m, d); use within t = -b±√(b 2 float c = dot(m, m) --c)s. r * s. r; } t● Q Return false if the ray origin is outside of the sphere (i. e. c>0) and pointing away from the if (c (b>0) > 0. 0 f && b > 0. 0 f) return false; sphere If the discriminant float discr = b*b - c; is negative, i. e. No if (discr < 0. 0 f) return false; real solutions, then the ray misses t = -b - sqrt(discr); sphere if (t < 0. 0 f) t = 0. 0 f; Determine the smallest (nonnegative) value of t which q = p + t * d; gives the nearest point of return true; intersection. If negative, then clamp to zero (ray started within sphere) r C●

ed ect r i g D din a e r DIRECTED READING Directed reading on primitive intersection

• Read Chapter 5 of Real Time Collision Detection: o pp 156 -174 for primitive intersection Directed reading tests ed ect r i g D din rea o pp 175 -200 for line, ray and segment intersection o pp 201 -231 for dynamic and other forms of intersection test • Related papers can be found from: http: //realtimecollisiondetection. net/books/rtcd/references/

Summary Today we explored: ü Basic primitive intersection tests ü Separating axis theory ü Sample plane and ray intersection tests : o d o T cted e r i d e h t d a e üR material he t g n i d a e r r e üAft ave h , l a i r e t a m directed is the s i h t f i r e d n a po you l a i r e t a m f o type ore l p x e o t e k i l would t. c e j o r p a n i h t wi