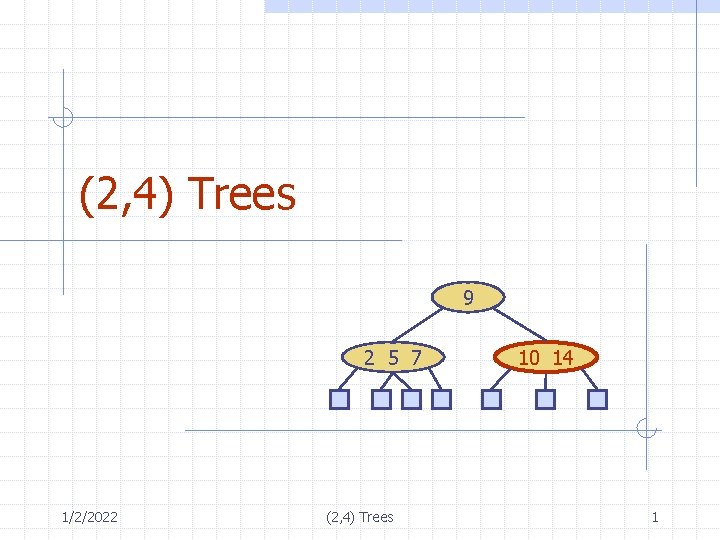
2 4 Trees 9 2 5 7 122022

(2, 4) Trees 9 2 5 7 1/2/2022 (2, 4) Trees 10 14 1

Outline and Reading Multi-way search tree (§ 3. 3. 1) n n Definition Search (2, 4) tree (§ 3. 3. 2) n n Definition Search Insertion Deletion Comparison of dictionary implementations 1/2/2022 (2, 4) Trees 2

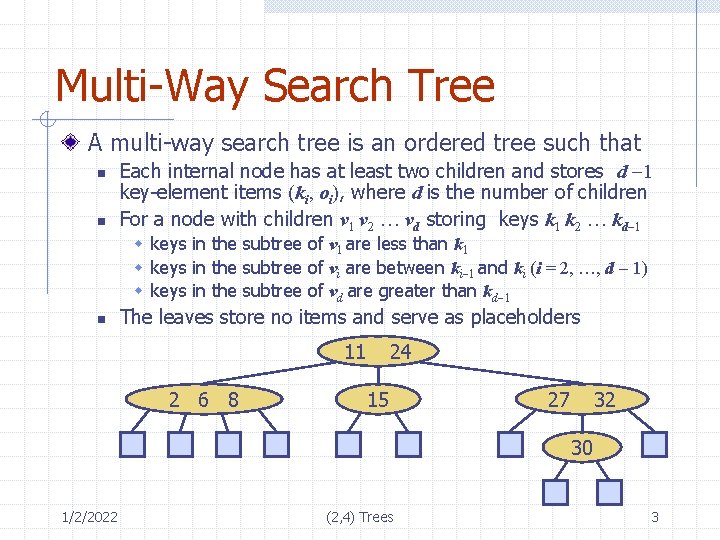
Multi-Way Search Tree A multi-way search tree is an ordered tree such that n n Each internal node has at least two children and stores d -1 key-element items (ki, oi), where d is the number of children For a node with children v 1 v 2 … vd storing keys k 1 k 2 … kd-1 w keys in the subtree of v 1 are less than k 1 w keys in the subtree of vi are between ki-1 and ki (i = 2, …, d - 1) w keys in the subtree of vd are greater than kd-1 n The leaves store no items and serve as placeholders 11 2 6 8 24 15 27 32 30 1/2/2022 (2, 4) Trees 3

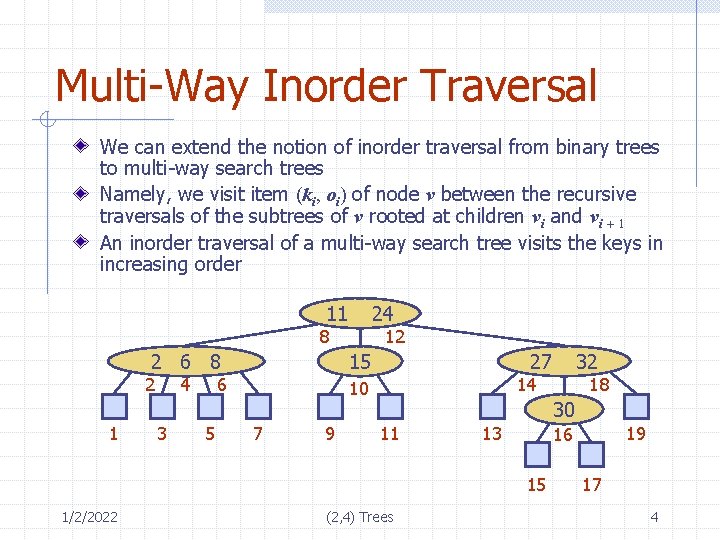
Multi-Way Inorder Traversal We can extend the notion of inorder traversal from binary trees to multi-way search trees Namely, we visit item (ki, oi) of node v between the recursive traversals of the subtrees of v rooted at children vi and vi + 1 An inorder traversal of a multi-way search tree visits the keys in increasing order 11 24 8 2 6 8 2 1 4 3 15 6 5 12 27 14 10 7 9 18 30 11 13 (2, 4) Trees 19 16 15 1/2/2022 32 17 4

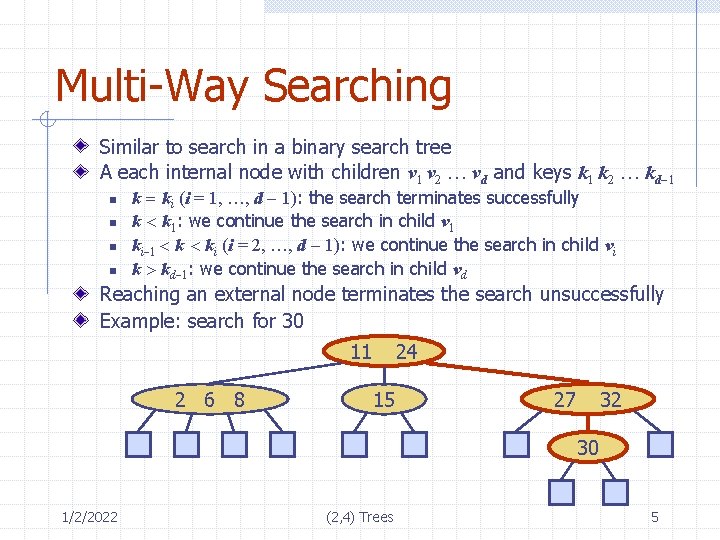
Multi-Way Searching Similar to search in a binary search tree A each internal node with children v 1 v 2 … vd and keys k 1 k 2 … kd-1 n n k = ki (i = 1, …, d - 1): the search terminates successfully k < k 1: we continue the search in child v 1 ki-1 < ki (i = 2, …, d - 1): we continue the search in child vi k > kd-1: we continue the search in child vd Reaching an external node terminates the search unsuccessfully Example: search for 30 11 2 6 8 24 15 27 32 30 1/2/2022 (2, 4) Trees 5

(2, 4) Tree A (2, 4) tree (also called 2 -4 tree or 2 -3 -4 tree) is a multi-way search with the following properties n n Node-Size Property: every internal node has at most four children Depth Property: all the external nodes have the same depth Depending on the number of children, an internal node of a (2, 4) tree is called a 2 -node, 3 -node or 4 -node 10 15 24 2 8 1/2/2022 12 (2, 4) Trees 18 27 32 6

Height of a (2, 4) Tree Theorem: A (2, 4) tree storing n items has height Θ(log n) Proof: n n n 1/2/2022 Let h be the height of a (2, 4) tree with n items By depth property, we can have at most 4 nodes at depth 1, at most 42 at depth 2, etc. Thus number of external nodes is at most 4 h Also by depth property, have at least 2 nodes at depth 1, 22 nodes at depth 2, and in general at least 2 h external nodes. Fact: a multiway search tree storing n items has n+1 external nodes (homework: C-3. 16) Thus, 2 h≤n+1 and n+1≤ 4 h Taking logs gives h≤log(n+1) and log(n+1) ≤ 2 h which proves theorem. (2, 4) Trees 7

Height of a (2, 4) Tree Searching in a (2, 4) tree with n items takes O(log n) time n A direct consequence of our height theorem. depth items 0 1 1 2 h-1 2 h-1 h 0 1/2/2022 (2, 4) Trees 8

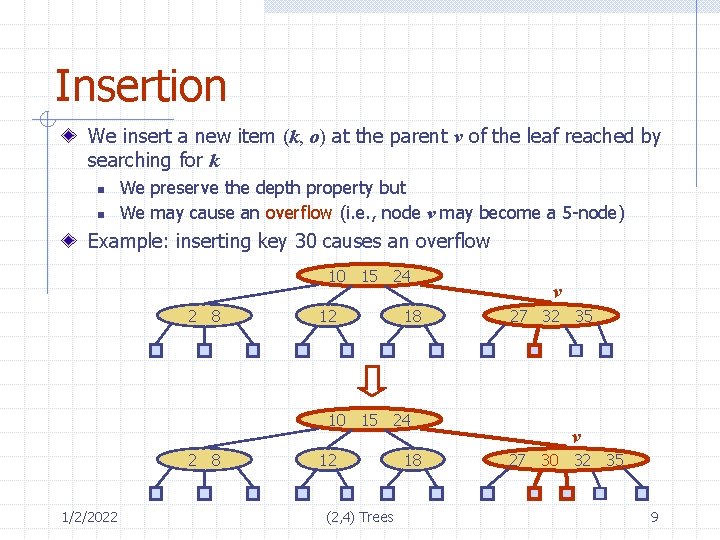
Insertion We insert a new item (k, o) at the parent v of the leaf reached by searching for k n n We preserve the depth property but We may cause an overflow (i. e. , node v may become a 5 -node) Example: inserting key 30 causes an overflow 10 15 24 2 8 12 18 10 15 24 2 8 1/2/2022 12 (2, 4) Trees 18 v 27 32 35 v 27 30 32 35 9

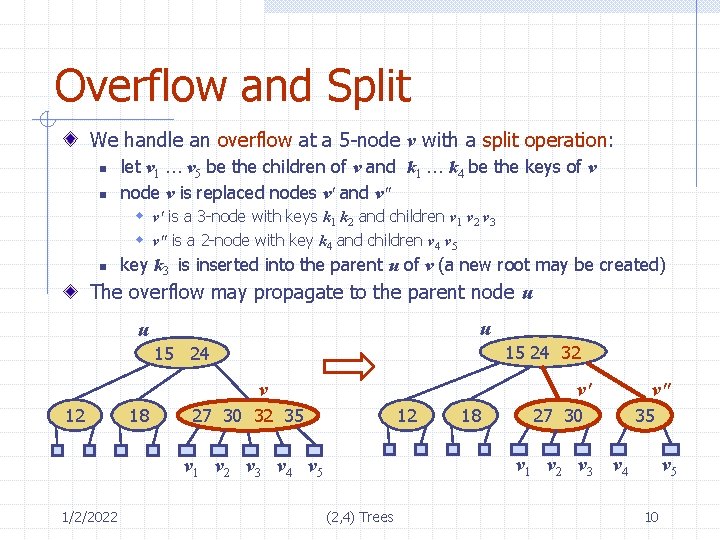
Overflow and Split We handle an overflow at a 5 -node v with a split operation: n n let v 1 … v 5 be the children of v and k 1 … k 4 be the keys of v node v is replaced nodes v' and v" w v' is a 3 -node with keys k 1 k 2 and children v 1 v 2 v 3 w v" is a 2 -node with key k 4 and children v 4 v 5 n key k 3 is inserted into the parent u of v (a new root may be created) The overflow may propagate to the parent node u u u 15 24 32 15 24 v 12 18 v' 27 30 32 35 12 27 30 35 v 1 v 2 v 3 v 4 v 5 1/2/2022 18 v" (2, 4) Trees v 5 10

Analysis of Insertion Let T be a (2, 4) tree with n items Algorithm insert. Item(k, o) 1. We search for key k to locate the insertion node v n n 2. We add the new item (k, o) at node v 3. while overflow(v) if is. Root(v) create a new empty root above v v split(v) n n Tree T has O(log n) height Step 1 takes O(log n) time because we visit O(log n) nodes Step 2 takes O(1) time Step 3 takes O(log n) time because each split takes O(1) time and we may perform O(log n) splits Thus, an insertion in a (2, 4) tree takes O(log n) time 1/2/2022 (2, 4) Trees 11

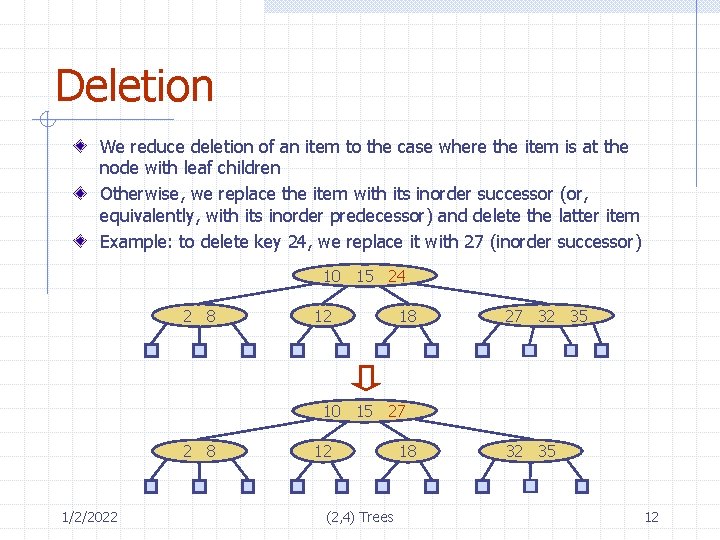
Deletion We reduce deletion of an item to the case where the item is at the node with leaf children Otherwise, we replace the item with its inorder successor (or, equivalently, with its inorder predecessor) and delete the latter item Example: to delete key 24, we replace it with 27 (inorder successor) 10 15 24 2 8 12 18 27 32 35 10 15 27 2 8 1/2/2022 12 (2, 4) Trees 18 32 35 12

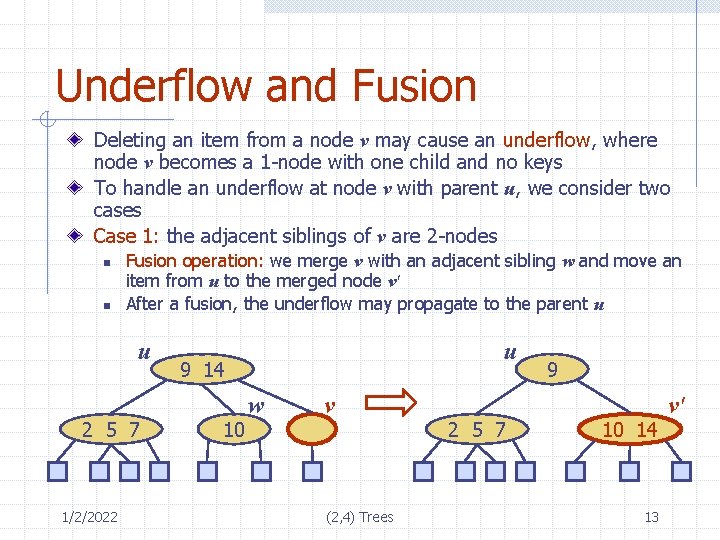
Underflow and Fusion Deleting an item from a node v may cause an underflow, where node v becomes a 1 -node with one child and no keys To handle an underflow at node v with parent u, we consider two cases Case 1: the adjacent siblings of v are 2 -nodes n n Fusion operation: we merge v with an adjacent sibling w and move an item from u to the merged node v' After a fusion, the underflow may propagate to the parent u u 2 5 7 1/2/2022 u 9 14 10 w v (2, 4) Trees 2 5 7 9 10 14 13 v'

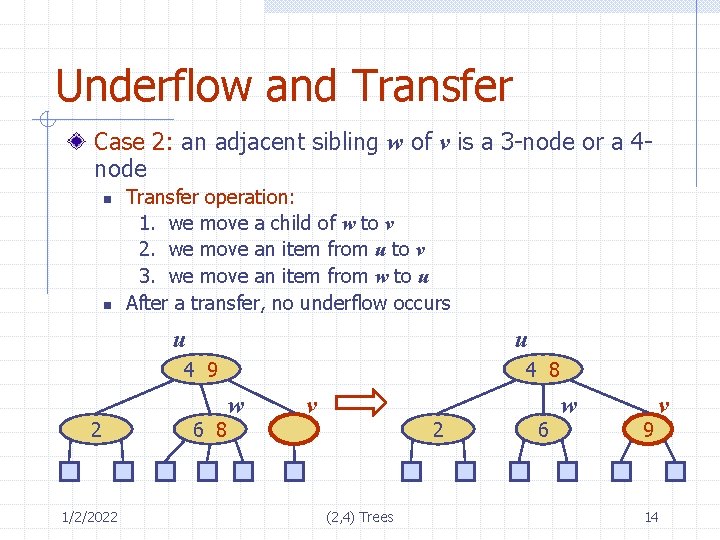
Underflow and Transfer Case 2: an adjacent sibling w of v is a 3 -node or a 4 node n n Transfer operation: 1. we move a child of w to v 2. we move an item from u to v 3. we move an item from w to u After a transfer, no underflow occurs u u 4 9 2 1/2/2022 6 8 4 8 w v 2 (2, 4) Trees 6 w 9 v 14

Analysis of Deletion Let T be a (2, 4) tree with n items n Tree T has O(log n) height In a deletion operation n We visit O(log n) nodes to locate the node from which to delete the item We handle an underflow with a series of O(log n) fusions, followed by at most one transfer Each fusion and transfer takes O(1) time Thus, deleting an item from a (2, 4) tree takes O(log n) time 1/2/2022 (2, 4) Trees 15

Implementing a Dictionary Comparison of efficient dictionary implementations Hash Table Skip List (2, 4) Tree 1/2/2022 Search Insert Delete 1 1 1 expected log n high prob. w randomized insertion w simple to implement log n worst-case w complex to implement (2, 4) Trees Notes w no ordered dictionary methods w simple to implement 16

Red-Black Trees v 6 8 3 4 1/2/2022 (2, 4) Trees z 17

Outline and Reading From (2, 4) trees to red-black trees (§ 3. 3. 3) Red-black tree (§ 3. 3. 3) n n n Definition Height Insertion w restructuring w recoloring n Deletion w restructuring w recoloring w adjustment 1/2/2022 (2, 4) Trees 18

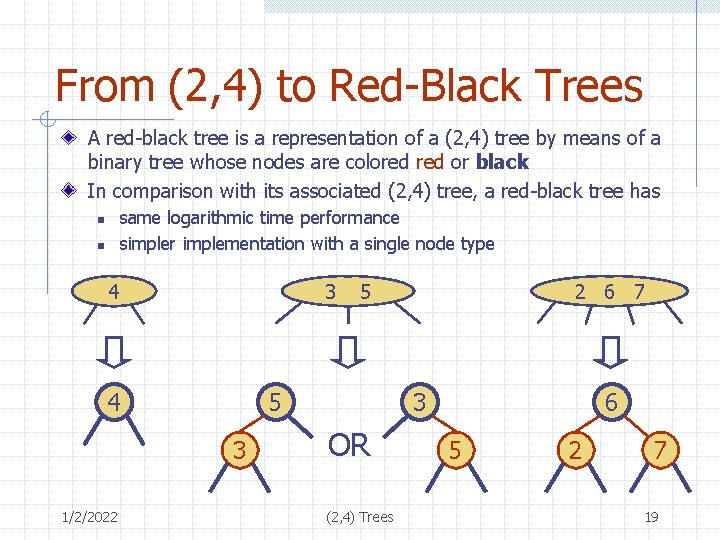
From (2, 4) to Red-Black Trees A red-black tree is a representation of a (2, 4) tree by means of a binary tree whose nodes are colored or black In comparison with its associated (2, 4) tree, a red-black tree has same logarithmic time performance simpler implementation with a single node type n n 4 3 4 5 3 1/2/2022 5 2 6 7 3 OR (2, 4) Trees 6 5 2 7 19

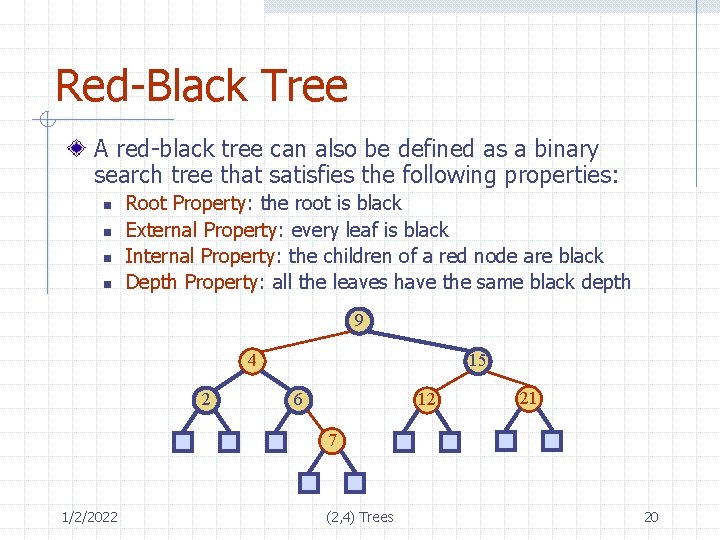
Red-Black Tree A red-black tree can also be defined as a binary search tree that satisfies the following properties: n n Root Property: the root is black External Property: every leaf is black Internal Property: the children of a red node are black Depth Property: all the leaves have the same black depth 9 4 2 15 6 12 21 7 1/2/2022 (2, 4) Trees 20

Height of a Red-Black Tree Theorem: A red-black tree storing n items has height O(log n) Proof: n The height of a red-black tree is at most twice the height of its associated (2, 4) tree, which is O(log n) The search algorithm for a binary search tree is the same as that for a binary search tree By the above theorem, searching in a red-black tree takes O(log n) time 1/2/2022 (2, 4) Trees 21

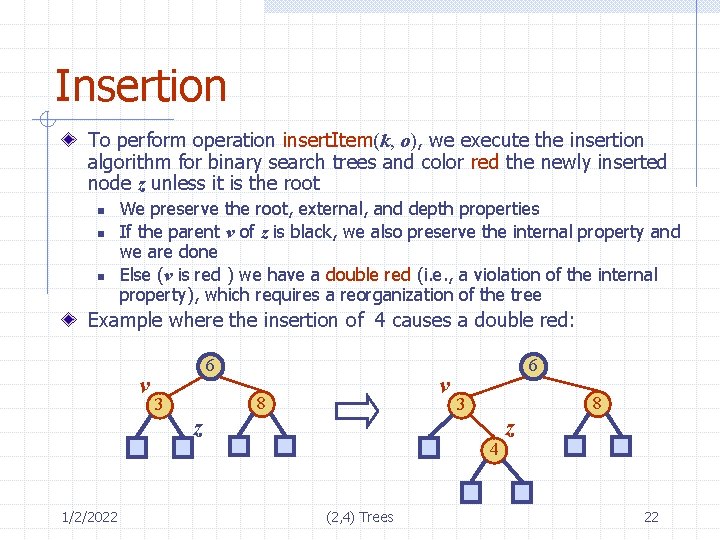
Insertion To perform operation insert. Item(k, o), we execute the insertion algorithm for binary search trees and color red the newly inserted node z unless it is the root n n n We preserve the root, external, and depth properties If the parent v of z is black, we also preserve the internal property and we are done Else (v is red ) we have a double red (i. e. , a violation of the internal property), which requires a reorganization of the tree Example where the insertion of 4 causes a double red: v 1/2/2022 6 3 v 8 z 6 8 3 4 (2, 4) Trees z 22

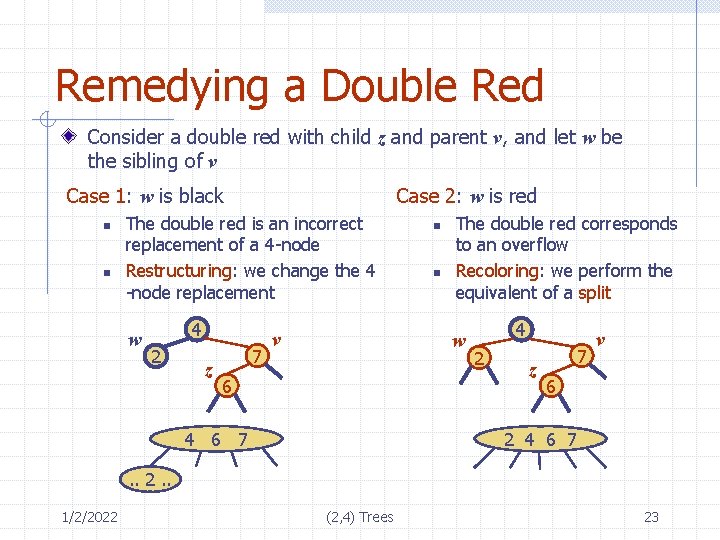
Remedying a Double Red Consider a double red with child z and parent v, and let w be the sibling of v Case 1: w is black n n Case 2: w is red The double red is an incorrect replacement of a 4 -node Restructuring: we change the 4 -node replacement w 4 2 z 7 v n n The double red corresponds to an overflow Recoloring: we perform the equivalent of a split w 6 4 6 7 4 2 z 7 v 6 2 4 6 7 . . 2. . 1/2/2022 (2, 4) Trees 23

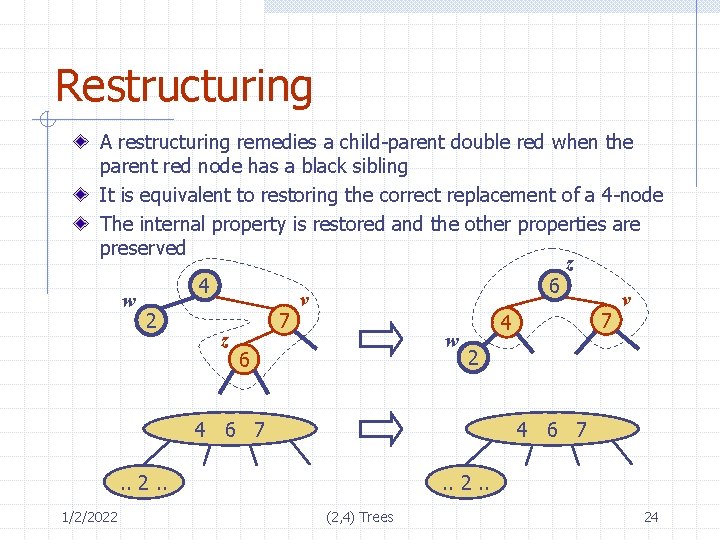
Restructuring A restructuring remedies a child-parent double red when the parent red node has a black sibling It is equivalent to restoring the correct replacement of a 4 -node The internal property is restored and the other properties are preserved z 6 4 v v w 7 7 2 4 z w 2 6 4 6 7 . . 2. . 1/2/2022 . . 2. . (2, 4) Trees 24

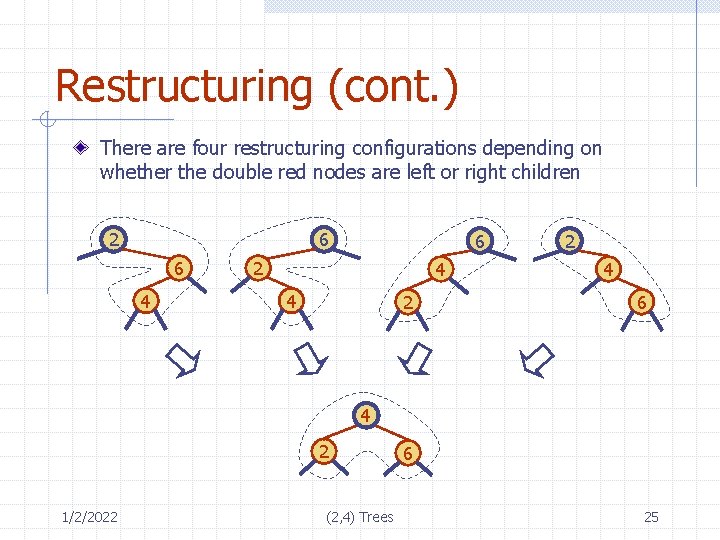
Restructuring (cont. ) There are four restructuring configurations depending on whether the double red nodes are left or right children 6 2 6 4 6 2 4 4 2 2 4 6 4 2 1/2/2022 (2, 4) Trees 6 25

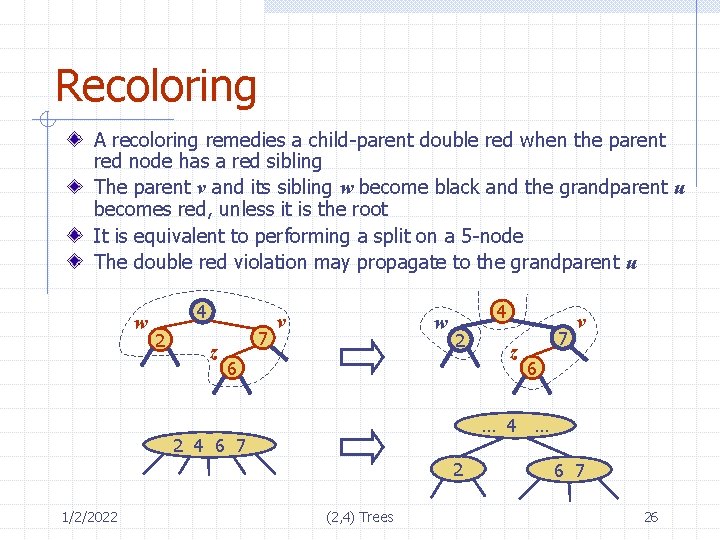
Recoloring A recoloring remedies a child-parent double red when the parent red node has a red sibling The parent v and its sibling w become black and the grandparent u becomes red, unless it is the root It is equivalent to performing a split on a 5 -node The double red violation may propagate to the grandparent u w 4 2 z 7 v w 4 2 6 7 6 … 4 … 2 4 6 7 2 1/2/2022 z v (2, 4) Trees 6 7 26

Analysis of Insertion Algorithm insert. Item(k, o) 1. We search for key k to locate the insertion node z 2. We add the new item (k, o) at node z and color z red 3. while double. Red(z) if is. Black(sibling(parent(z))) z restructure(z) return else { sibling(parent(z) is red } z recolor(z) 1/2/2022 (2, 4) Trees Recall that a red-black tree has O(log n) height Step 1 takes O(log n) time because we visit O(log n) nodes Step 2 takes O(1) time Step 3 takes O(log n) time because we perform n n O(log n) recolorings, each taking O(1) time, and at most one restructuring taking O(1) time Thus, an insertion in a redblack tree takes O(log n) time 27

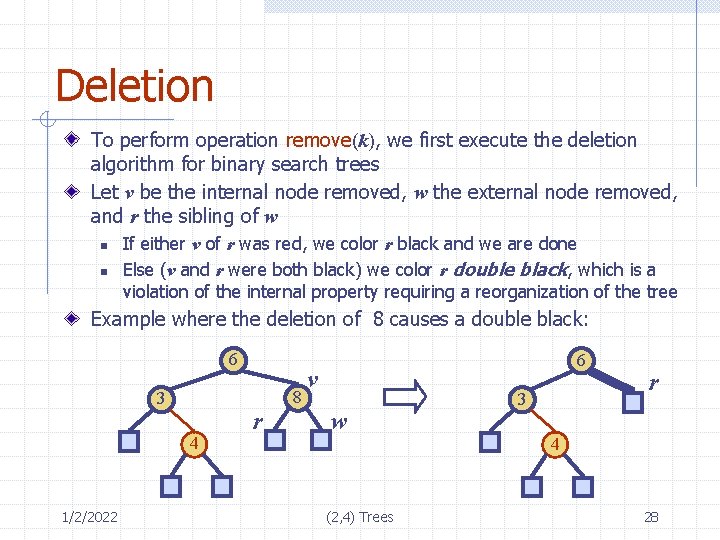
Deletion To perform operation remove(k), we first execute the deletion algorithm for binary search trees Let v be the internal node removed, w the external node removed, and r the sibling of w n n If either v of r was red, we color r black and we are done Else (v and r were both black) we color r double black, which is a violation of the internal property requiring a reorganization of the tree Example where the deletion of 8 causes a double black: 6 8 3 4 1/2/2022 r 6 v w (2, 4) Trees 3 r 4 28

Remedying a Double Black The algorithm for remedying a double black node w with sibling y considers three cases Case 1: y is black and has a red child n We perform a restructuring, equivalent to a transfer , and we are done Case 2: y is black and its children are both black n We perform a recoloring, equivalent to a fusion, which may propagate up the double black violation Case 3: y is red n We perform an adjustment, equivalent to choosing a different representation of a 3 -node, after which either Case 1 or Case 2 applies Deletion in a red-black tree takes O(log n) time 1/2/2022 (2, 4) Trees 29

Red-Black Tree Reorganization Insertion remedy double red Red-black tree action (2, 4) tree action result restructuring change of 4 -node representation double red removed recoloring split double red removed or propagated up Deletion remedy double black Red-black tree action (2, 4) tree action result restructuring transfer double black removed recoloring fusion double black removed or propagated up adjustment change of 3 -node representation restructuring or recoloring follows 1/2/2022 (2, 4) Trees 30