2 4 Reasoning with Properties of Algebra Goal

2. 4 Reasoning with Properties of Algebra

Goal 1: Using Properties from Algebra • Pg. 96 – – – – Addition property Subtraction property Multiplication property Division property Reflexive property Symmetric property Transitive property Substitution property If a = b, then a+c = b+c If a=b, then a-c=b-c If a=b, then ac=bc If a=b, then a c=b c a=a If a=b, then b=a If a=b and b=c, then a=c If a=b, then a can be substituted for b in any expression or equation.

Distributive Property • a (b + c) = ab + ac • Algebra Properties can be used to solve equations • Example: x + 3 = 7 By subtracting 3 from each side of the equation, you obtain 4.

Example 1: Writing Reasons Solve 5 x – 18 = 3 x +2 1. 5 x – 18 = 3 x + 2 2. 2 x – 18 = 2 3. 2 x = 20 4. x = 10 1. Given 2. Subtraction property 3. Addition property 4. Division property

Example 2: Writing Reasons • Solve 55 z – 3(9 z + 12)= -64 1. 2. 3. 4. 5. 55 z – 3(9 z + 12)= -64 55 z – 27 z – 36 = -64 28 z = -28 z = -1 1. 2. 3. 4. 5. Given Distributiveproperty Simplify Addition property Division property

Example 3: Using properties in Real Life • Before exercising, you should find your target heart rate. This is the rate at which you achieve an effective workout while not placing too much strain on your heart. Your target heart rate (r) –in beats per minute can be determined from your age (a)—in years using the equation a = 220 – 10/7 r.

Find the following: a. Solve the equation for r and write a reason for each step. b. Use the result to find the target heart rate for a 16 -year old. c. Find the target rate for the following ages: 20, 30, 40, 50, and 60. What happens to the target heart rate as a person gets older?

a. a = 220 – 10/7 r 1. 2. 3. 4. a = 220 – 10/7 r a + 10/7 r = 220 10/7 r = 220 – a r = 7/10(220 – a) 1. 2. 3. 4. Given Addition property Subtraction property Multiplication property

b. Using a = 16, the target rate is: 1. r = 7/10(220 – a) 2. r = 7/10(220 – 16) 3. r = 142. 8 The target rate for a 16 year old is about 143 beats per minute 1. Given 2. Substitute 16 for a 3. Simplify
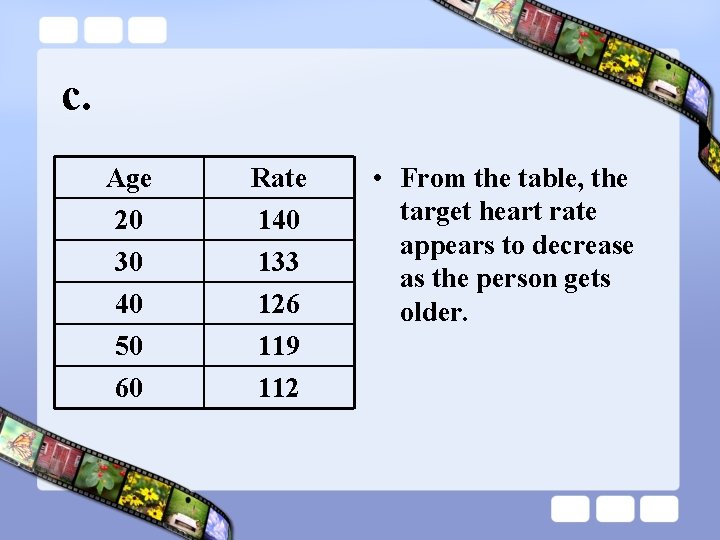
c. Age 20 30 Rate 140 133 40 50 60 126 119 112 • From the table, the target heart rate appears to decrease as the person gets older.

Goal 2: Using Properties of Length and Measure Segment Length • Reflexive: AB = AB • Symmetric: If AB=CD, then CD=BA • Transitive: If AB=CD and CD=EF, then AB=EF.

Angle Measure Properties • Reflexive: m A=m A • Symmetric: If m A = m B, then m B = m A. • Transitive: If m A = m B and m B = m C, then m A = m C.

Example 4: Using properties of length 1. AB = CD 1. Given 2. 3. 4. 5. 2. Addition property 3. Segment addition postulate 4. Segment addition postulate 5. Substitution property AB + BC = BC + CD AC = AB + BC BD = BC + CD AC = BD

Example 5: Using properties of measure 1. 2. 3. 4. 5. 6. 7. m 1 + m 2 = 66 m 1 + m 2+m 3 = 99 66 + m 3 = 99 m 3 = 33 m 3 = m 1, m 1 = m 4 m 3=m 4 m 4 = 33 1. 2. 3. 4. 5. 6. 7. Given Substitution Subtraction Given Transitive Substitution
- Slides: 14