2 4 PRIMITIVETESTS CLOSEST POINT Closest point forms

2. 4. PRIMITIVETESTS -CLOSEST POINT Closest point forms of intersection detection

Finding the closest point between two objects provides a number of benefits. If positive, the objects are separated, if negative, the objects are interpenetrating (and knowledge of the closest point can be used to provide contact information). Closest point forms of intersection detection Two different approaches can be used to find the minimum point: • Formulate the test as a minimisation problem and solve it using calculus. • Use the geometric properties of the objects to geometrically derive the closest point (considered here). cord of Keeping a reo ints the closest p objects between two can often be y incrementallat a low maintained cost (object providing coherency), testing. fast collision

• Closest Point on Line Segment to Point • Closest Point on AABB to Point • Closest Point on OBB to Point • Closest Point on Triangle to Point • Closest Point on Convex Polyhedron to Point • Closest Points of Two Lines • Closest Points of Two Line Segments • Closest Points of a Line Segment and a Triangle • Closest Points of Two Triangles Forms of closest point test Two illustrative forms of closest point test are explored next.

POINT TOOBB Closest point between an OBB and a Point

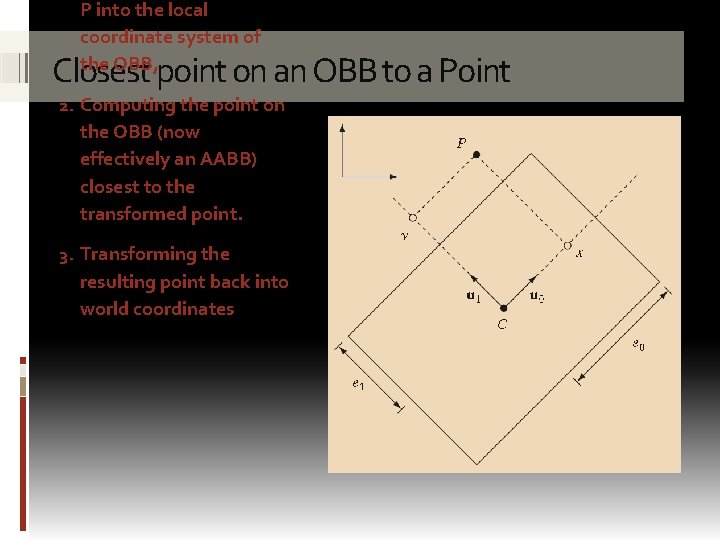
Consider an OBB with centre point C, orthogonal unit vectors (u 0, u 1, u 2) and half-width distances (e 0, e 1, e 2) and a point P. Closest point on an OBB to a Point

P into the local coordinate system of the OBB, Closest point on an OBB to a Point 2. Computing the point on the OBB (now effectively an AABB) closest to the transformed point. 3. Transforming the resulting point back into world coordinates

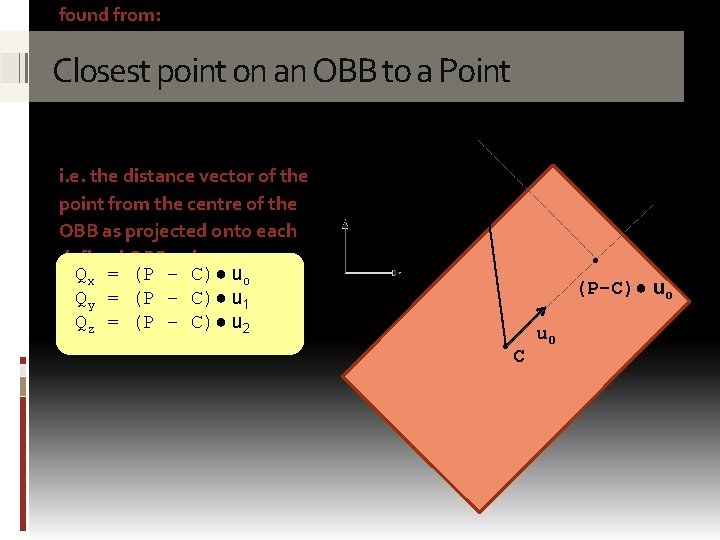
found from: Closest point on an OBB to a Point P ● i. e. the distance vector of the point from the centre of the OBB as projected onto each defined OBB axis Qx = (P – C)● uo Qy = (P – C)● u 1 Qz = (P – C)● u 2 P-C ● (P-C)● uo ● C u 0

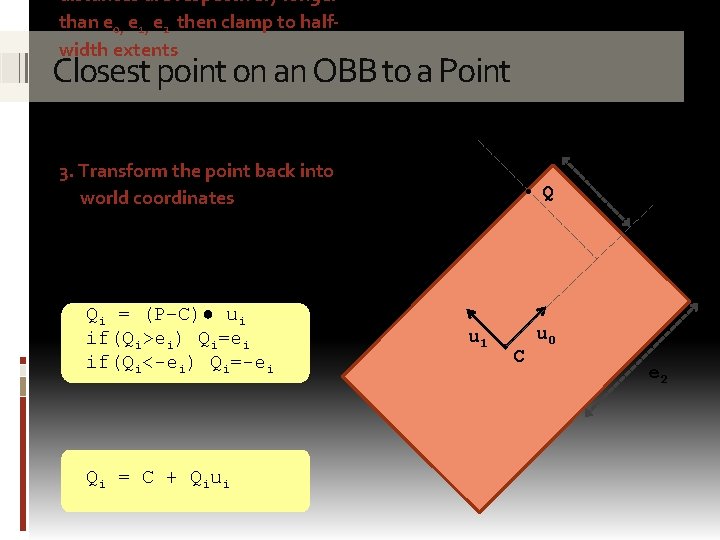
distances are respectively longer than e 0, e 1, e 2 then clamp to halfwidth extents Closest point on an OBB to a Point P ● 3. Transform the point back into world coordinates Qi = (P–C)● ui if(Qi>ei) Qi=ei if(Qi<-ei) Qi=-ei Qi = C + Qiui ● u 1 ● C Q e 1 u 0 e 2

Expressed as code: on an OBB to a Point Closest point Closest. Point. To. OBB(Point point, OBB box, out Point closest. Pt) { Vector distance = point- box. centre; Initially set closest point as box closest. Pt = box. centre; centre for (int i = 0; i < 3; i++) { Iterate over box Determine float length = Dot(distance, axis box. axis[i]); projection along axis Clamp if if (length > box. extent[i]) length = box. extent[i]; needed if (length < -box. extent[i]) length = -box. extent[i]; closest. Pt += length * box. axis[i]; Build world location component by moving } determine distance along } OBB axis

The separation (actual or squared) can then be determined simply as: Closest point on an OBB to a Point float distance = (closest. Pt – point). length() Somewha t obviously , compone if all n closest OB ts of the (expresse B point d space) ar in OBB e the half- less than w extents, t idth h point is w en the ithin the OBB.

POINT TOTRIANGLE Closest point between a Triangle and a Point

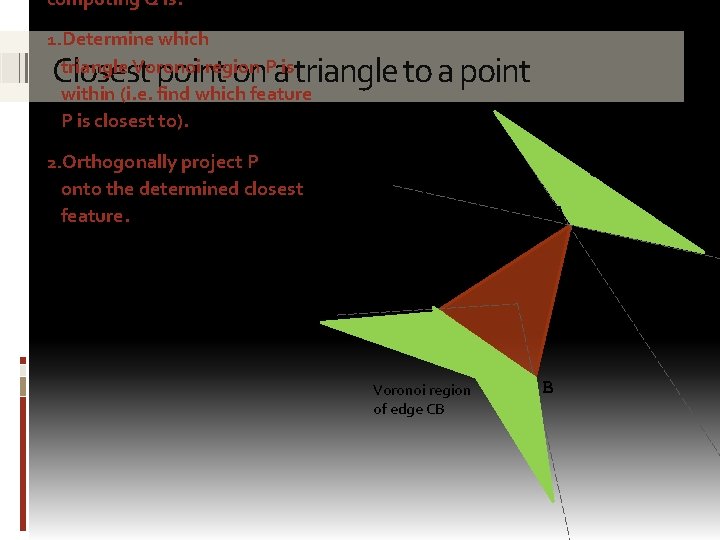
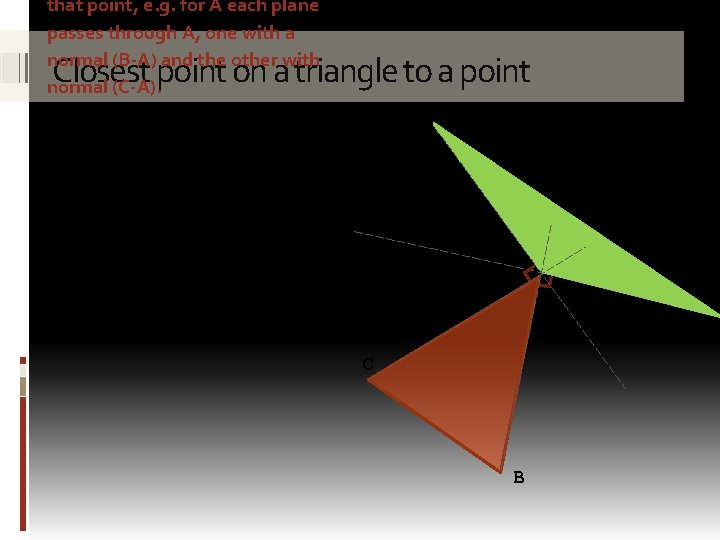
computing Q is: 1. Determine which triangle Voronoi region P is within (i. e. find which feature P is closest to). Closest point on a triangle to a point Vo ro 2. Orthogonally project P onto the determined closest feature. no A C Voronoi region of edge CB B i re A gio n of ve rte x. A

that point, e. g. for A each plane passes through A, one with a normal (B-A) and the other with normal (C-A). Closest point on a triangle to a point Vo ro no i re gio n A A C B of ve rte x A

and R is the projection of P onto the triangle’s plane, i. e. R = P – tn some for t, the barycentric coordinates of R (R = u. A + v. B + w. C) are given by: A Closest point on a triangle to a point C Voronoi region of edge CB n = rab rbc rca abc u = (B-A)×(C-A) = n ● ((A-P)×(B-P)) = n ● ((B-P)×(C-P)) = n ● ((C-P)×(A-P)) = rab + rbc + rca rbc/abc, v = rca/abc, w = rab/abc Aside: the barycentric coordinates of R are given as the ratios of the signed areas of triangles RAB, RBC, and RCA to the signed area of ABC B

1. Calculated area of the barycentric region must be <= 0 (i. e. for AB, rab <= 0) Closest point on a triangle to a point 2. The point must be within the positive half-spaces of the planes (assuming an edge AB): (X-A)●(B-A) = 0 and (X-B)●(A -B) = 0 (X-B)● (A-B) > 0 A C B Aside: It is notto test if sufficient just B, in that P is outside A with an for a triangle t A, P obtuse angle ade AB could be outsi e located and actually bi region of in the Vorono gure). edge CA (see fi B (X-A)● (B-A) > 0

Closest point on a Triangle to a Points ABC defined the triangle, point P is the source point, point Q is the closest Closest. Point. To. Triangle( triangle point to P Point a, Point b, Point c, Point p, out Point q { Build edge Vector ab = b – a, ac = c – a, bc = c - b; vectors Determine the parametric position s for the projection of P onto AB (i. e. P’ = A+s*AB, where s = snom/ (snom+sdenom), and then parametric position snom t for P =projected float Dot(p onto - a, ACab), sdenom = Dot(p - b, a - b); float tnom = Dot(p - a, ac), tdenom = Dot(p - c, a - c); if (snom <= 0. 0 f && tnom <= 0. 0 f) return a; Vertex Voronoi region hit early Parametric position u for P projected out onto BCunom = Dot(p - b, bc), udenom = Dot(p - c, b - c); float if (sdenom <= 0. 0 f && unom <= 0. 0 f) return b; if (tdenom <= 0. 0 f && udenom <= 0. 0 f) return c; Aside: the of P projection om point onto AB fr (B-A) and A is: (P-A)●to BA is: from P on). Added (P-B)●(A-B hey sum together tgth of AB to the len

Closest point on a Triangle to a Point Determine if P is outside (or on) edge AB by finding the area formed by vectors PA, PB and the triangle normal. A scalar Vector n = is. Cross(b - a, c - a); triple product used. float vc = Dot(n, Cross(a - p, b - p)); If P is outside of AB (signed area <= 0) and within Voronoi feature region, then return projection of P onto AB if (vc <= 0. 0 f && snom >= 0. 0 f && sdenom >= 0. 0 f) return a + snom / (snom + sdenom) * ab; Repeat the same test for P float onto BCva = Dot(n, Cross(b if (va <= 0. 0 f && unom >= return b + unom / (unom + Repeat the same test for P float onto CAvb = Dot(n, Cross(c if (vb <= 0. 0 f && tnom >= return a + tnom / (tnom + - p, c - p)); 0. 0 f && udenom >= 0. 0 f) udenom) * bc; - p, a - p)); 0. 0 f && tdenom >= 0. 0 f) tdenom) * ac; P must project onto inside face. Find closest point using the float u =coordinates va / (va + vb + vc); barycentric float v = vb / (va + vb + vc); float w = 1. 0 f - u - v; // = vc / (va + vb + vc) return u * a + v * b + w * c; } Lagrange Aside: The × b) · (c × d) = identity (a (a · d)(b · c) − (a · c)(b · sde)d to express can be u scalar triple three in a manner products be calculated that can kly. more quic

ed ect r i g D din a e r DIRECTED READING Directed mathematical reading

Directed reading • Read Chapter 5 (pp 125155) of Real Time Collision Detection ed ect r i g D din rea • Related papers can be found from: http: //realtimecollisiondetection. net/books/rtcd/references/

Summary Today we explored: ü Notion of closest point forms of intersection testing. ü Closest point to an OBB or triangle : o d o T cted e r i d e h t d a e üR material he t g n i d a e r r e üAft ave h , l a i r e t a m directed is the s i h t f i r e d n a po you l a i r e t a m f o type ore l p x e o t e k i l would t. c e j o r p a n i h t wi