2 4 More Modeling with Functions Model data

2. 4 More Modeling with Functions • Model data with a linear function • Evaluate and graph piecewise-defined functions • Evaluate and graph the greatest integer function • Use direct variation to solve problems Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Modeling with a Linear Function To model a quantity that is changing at a constant rate with f(x) = mx + b, the following formula may be used. f(x) = (constant rate of change)x + initial amount The constant rate of change corresponds to the slope of the graph of f, and the initial amount corresponds to the y-coordinate of the y-intercept. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

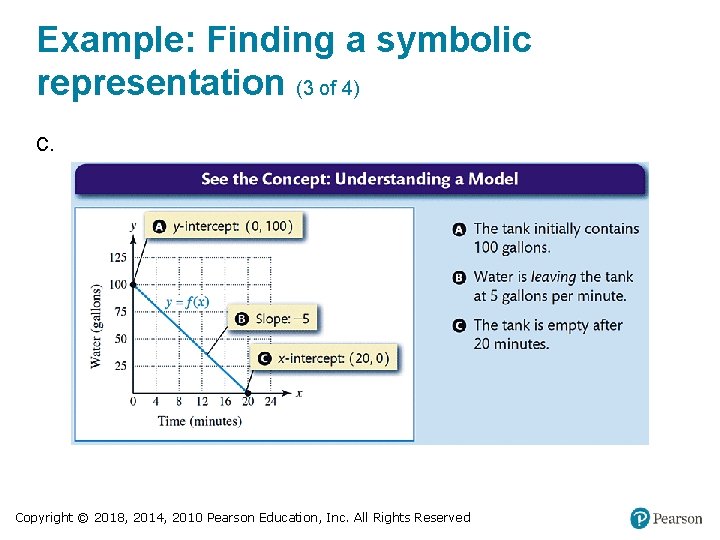
Example: Finding a symbolic representation (1 of 4) A 100 -gallon water tank, initially full of water, is being drained at a rate of 5 gallons per minute. a. Write a formula for a linear function f that models the number of gallons of water in the tank after x minutes. b. How much water is in the tank after 4 minutes? c. Graph f. Identify the x- and y-intercepts and interpret each. d. Discuss the domain and range of f. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Finding a symbolic representation (2 of 4) Solution a. Water in tank decreasing at 5 gal/min, so constant rate of change is − 5. The initial amount of water is 100 gal. f(x) = − 5 x + 10 b. After 4 min the tank contains: f(4) = − 5(4) + 100 = 800 gal Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Finding a symbolic representation (3 of 4) c. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Finding a symbolic representation (4 of 4) d. From the graph: the domain of f must be restricted to 0 ≤ x ≤ 20. For example, 21 is not in the domain of ƒ because f(21) = − 5(21) + 100 = − 5; the tank cannot hold − 5 gallons. Similarly, − 1 is not in the domain of ƒ because f(− 1) = − 5(− 1) + 100 = 105; the tank holds at most 100 gallons. The range is between 0 and 100 gallons. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Piecewise-Defined Functions A function f that models data and is defined on pieces of its domain is called a piecewise-defined function. If each piece is linear, the functions is a piecewiselinear function. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

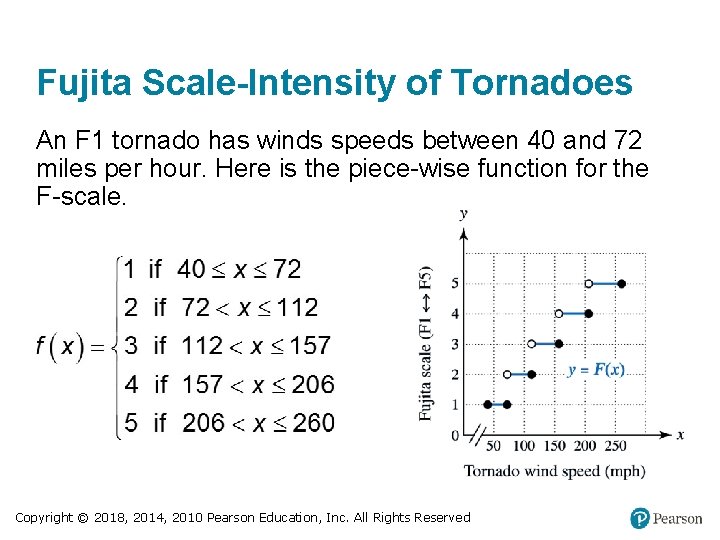
Fujita Scale-Intensity of Tornadoes An F 1 tornado has winds speeds between 40 and 72 miles per hour. Here is the piece-wise function for the F-scale. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

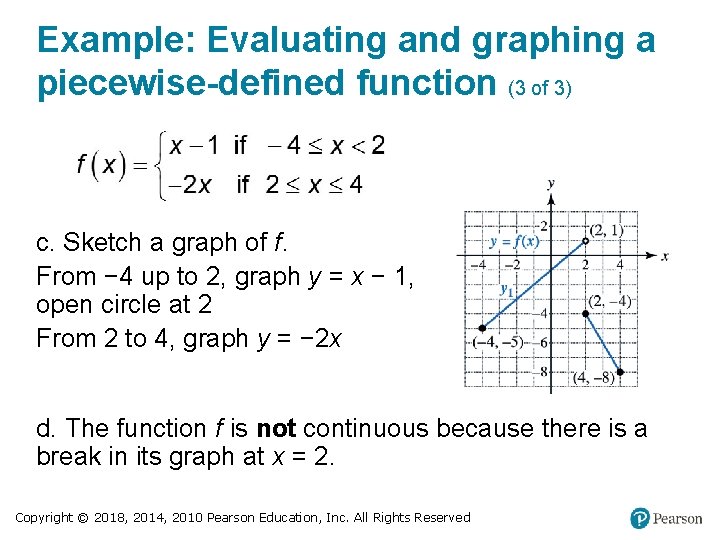
Example: Evaluating and graphing a piecewise-defined function (1 of 3) Use f(x) to complete the following: a. What is the domain of f ? b. Evaluate f(− 3), f(2), f(4), and f(5). c. Sketch a graph of f. d. Is f a continuous function on its domain? Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Evaluating and graphing a piecewise-defined function (2 of 3) Solution a. Function f is defined for − 4 ≤ x < 2 or 2 ≤ x ≤ 4. The domain is D = {x | − 4 ≤ x ≤ 4}, or [− 4, 4]. b. f(– 3) = − 3 − 1 = − 4 f(2) = − 2 · 2 = − 4 f(4) = − 2 · 4 = − 8 f(5) is undefined (5 is not in the domain) Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Evaluating and graphing a piecewise-defined function (3 of 3) c. Sketch a graph of f. From − 4 up to 2, graph y = x − 1, open circle at 2 From 2 to 4, graph y = − 2 x d. The function f is not continuous because there is a break in its graph at x = 2. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Greatest Integer Function Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

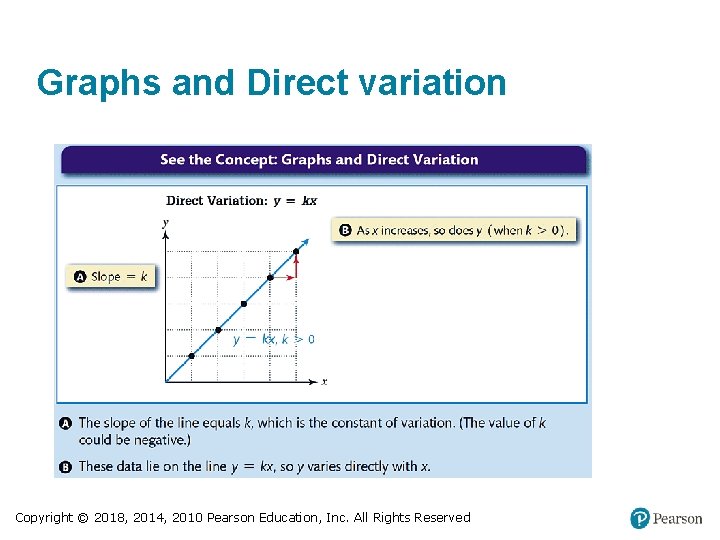
Direct Variation Let x and y denote two quantities. Then y is directly proportional to x, or y varies directly with x, if there exists a nonzero number k such that y = kx. The number k is called the constant of proportionality or the constant of variation. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Hooke’s Law (1 of 2) Hooke’s law states that the distance that an elastic spring stretches beyond its natural length is directly proportional to the amount of weight hung on the spring, as illustrated. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Hooke’s Law (2 of 2) This law is valid whether the spring is stretched or compressed. The constant of proportionality is called the spring constant. Thus if a weight or force F is applied and the spring stretches a distance x beyond its natural length, then the equation F = kx models this situation, where k is the spring constant. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Working with Hooke’s law (1 of 2) A 12 -pound weight is hung on a spring, and it stretches 2 inches. a. Find the spring constant. b. Determine how far the spring will stretch when a 19 pound weight is hung on it. Solution Let F = kx: F = 12 pounds, x = 2 inches. Thus 12 = k(2) so k = 6, and the spring constant equals 6. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Working with Hooke’s law (2 of 2) b. If F = 19 and F = 6 x, then Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Solving a Variation Problem (1 of 2) When solving a variation problem, the following steps can be used. STEP 1: Write the general equation for the type of variation problem that you are solving. STEP 2: Substitute given values in this equation so the constant of variation k is the only unknown value in the equation. Solve for k. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Solving a Variation Problem (2 of 2) STEP 3: Substitute the value of k in the general equation in Step 1. STEP 4: Use this equation to find the requested quantity. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Solving a direct variation problem (1 of 2) Let T vary directly with x, and suppose that T = 33 when x = 5. Find T when x = 31. Solution STEP 1: The equation for direct variation is T = kx. STEP 2: Substitute 33 for T, 5 for x. Then, solve for k. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Solving a direct variation problem (2 of 2) STEP 4: When x = 31, we have: T = 6. 6(31) = 204. 6 Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Graphs and Direct variation Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved