2 4 Modeling with Quadratic Functions Writing Quadratic

Writing Quadratic Equations • Given a point and the vertex -Use vertex form: •

Writing an equation using a vertex and a point Example 1. The graph shows

Writing an equation using a point and x-intercepts Example 2 A meteorologist creates a

Example 2 Continued b. What is the average rate of change in temperature over

Writing Equations to Model Data • When data have equally-spaced inputs, you can analyze

Writing an equation using 3 points Example 3 A baseball is thrown up in

Example 3 Continued A baseball is thrown up in the air. The table shows

Slides: 8

Download presentation

2. 4 Modeling with Quadratic Functions

Writing Quadratic Equations • Given a point and the vertex -Use vertex form: • Given a point and x-intercepts p and q -Use intercept form: • Given three points - Write and solve a system of three equations in three variables. Use the formula equation. to write each

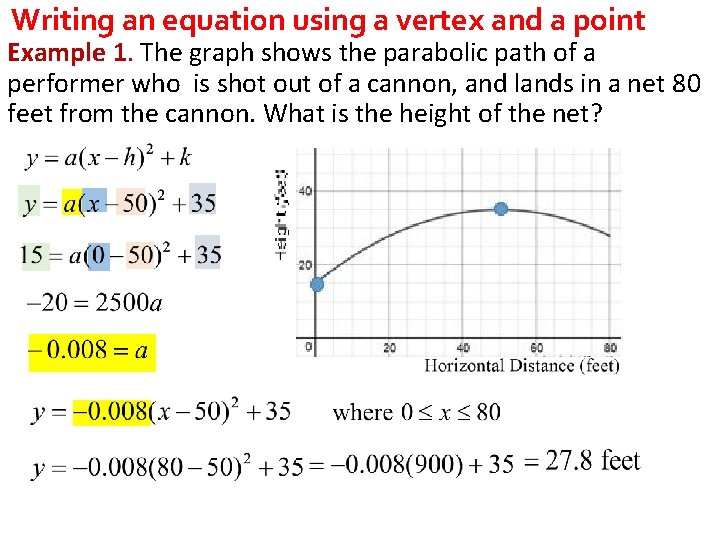
Writing an equation using a vertex and a point Example 1. The graph shows the parabolic path of a performer who is shot out of a cannon, and lands in a net 80 feet from the cannon. What is the height of the net?

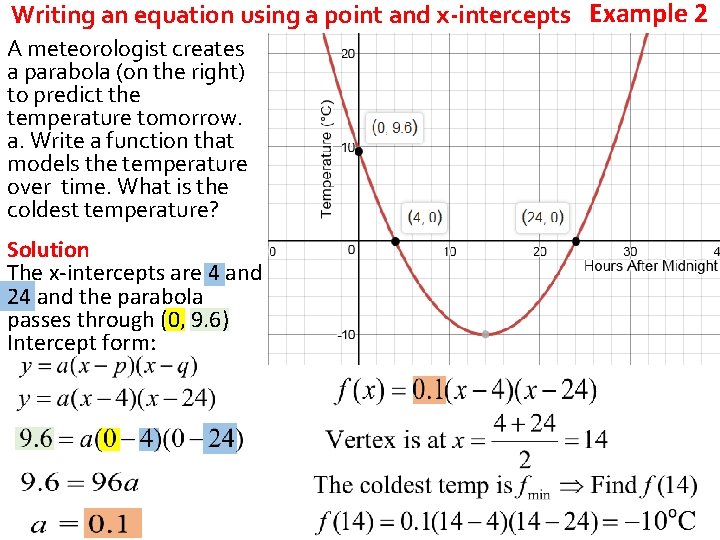
Writing an equation using a point and x-intercepts Example 2 A meteorologist creates a parabola (on the right) to predict the temperature tomorrow. a. Write a function that models the temperature over time. What is the coldest temperature? Solution The x-intercepts are 4 and 24 and the parabola passes through (0, 9. 6) Intercept form:

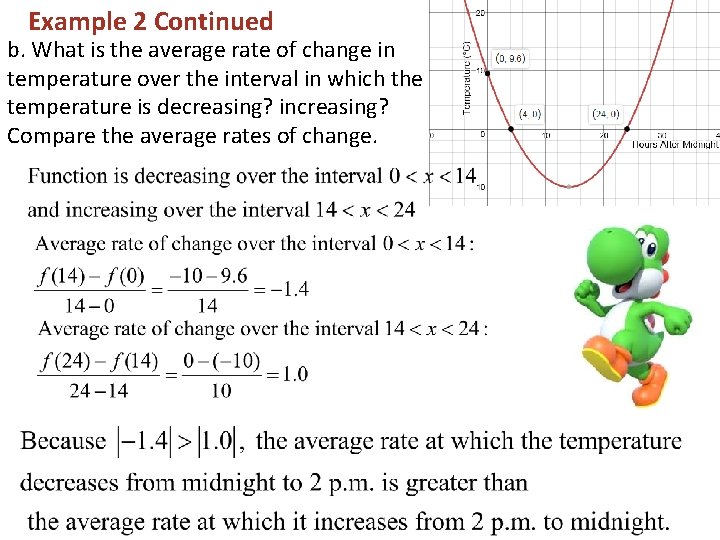
Example 2 Continued b. What is the average rate of change in temperature over the interval in which the temperature is decreasing? increasing? Compare the average rates of change.

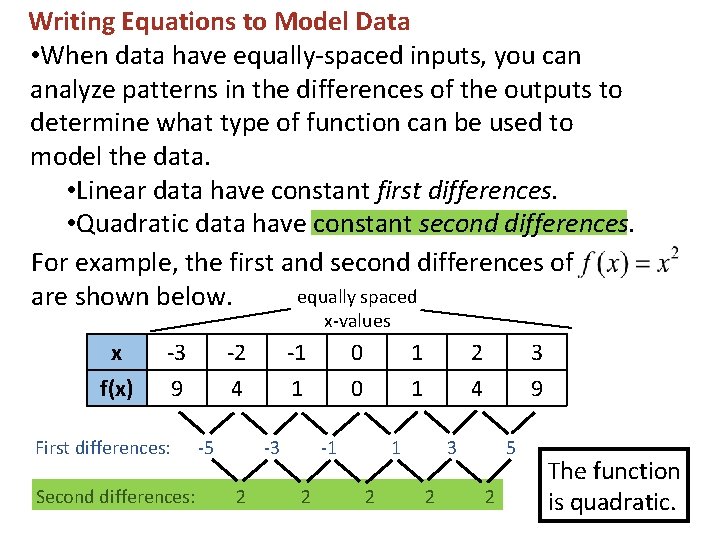
Writing Equations to Model Data • When data have equally-spaced inputs, you can analyze patterns in the differences of the outputs to determine what type of function can be used to model the data. • Linear data have constant first differences. • Quadratic data have constant second differences. For example, the first and second differences of equally spaced are shown below. x-values x f(x) -3 9 First differences: Second differences: -2 4 -5 -1 1 -3 2 0 0 1 1 -1 2 2 4 1 2 3 9 3 2 5 2 The function is quadratic.

Writing an equation using 3 points Example 3 A baseball is thrown up in the air. The table shows the heights y (in feet) of the baseball after x seconds. a. Write an equation for the path of the baseball. Solution Time, x 0 2 6 Three points (0, 6), (2, 22), and (6, 6) are given. Use Baseball height, y 6 22 6 the three points to write and solve a system of equations. Answer:

Example 3 Continued A baseball is thrown up in the air. The table shows the heights y (in feet) of the baseball after x seconds. b. Find the height of the baseball after 5 seconds. Solution Plug in 5 for x using the equation from part a. Time, x Baseball height, y 0 2 6 6 22 6 Answer: The height of the baseball after 5 seconds is 16 feet.