2 4 Modeling Motion in Matrices Objectives 1

2. 4 Modeling Motion in Matrices Objectives: 1. Use matrices to determine the coordinates of polygons under a given transformation.

2. 4 Modeling Motion in Matrices You can use simple matrices to describe motions which are called transformations. In geometry, you learned four basic transformations which are translations, reflections, rotations, and dilations. A polygon can be represented by a matrix. The x-coordinates are the first row of the matrix and the y-coordinates are the second row of the matrix. Suppose square ABCD has vertices A(-1, 3), B(3, 3), C(3, -1), and D( -1, - 1). Find the coordinates of the square after a translation of 1 unit left and 2 units down. Represent the vertices of the square ABCD as a matrix.

2. 4 Modeling Motion in Matrices Suppose square ABCD has vertices A(-1, 3), B(3, 3), C(3, -1), and D(-1, 1). Find the coordinates of the square after a translation of 1 unit left and 2 units down. Write the translation matrix. The translation matrix is the when added to the pre-image matrix you get the image matrix. It will have the same dimensions as the pre-image. The movement left/right is the first row and the movement up/down is the second row.

2. 4 Modeling Motion in Matrices Suppose square ABCD has vertices A(-1, 3), B(3, 3), C(3, -1), and D( -1, -1). Find the coordinates of the square after a translation of 1 unit left and 2 units down. Use the translation matrix to find the vertices of A’B’C’D’. This is the translated image of the square. This is A’B’C’D’. Then graph the pre-image ABCD and the image A’B’C’D’.

2. 4 Modeling Motion in Matrices Suppose square ABCD has vertices A(-1, 3), B(3, 3), C(3, -1), and D( -1, -1). Find the coordinates of the square after a translation of 1 unit left and 2 units down. Then graph the pre-image ABCD and the image A’B’C’D’.

2. 4 Modeling Motion in Matrices There are three lines over which figures are commonly reflected.

2. 4 Modeling Motion in Matrices Suppose square ABCD has vertices A(-1, 2), B(-4, 1), C(-3, -2), and D(0, -1). Find the image of the square after a reflection over the y-axis. First, write the vertices of the square as matrix.

2. 4 Modeling Motion in Matrices Suppose square ABCD has vertices A(-1, 2), B(-4, 1), C(-3, -2), and D(0, -1). Find the image of the square after a reflection over the y-axis. Choose the appropriate reflection matrix for the given reflection. Then multiple the pre-image and reflection matrix. Be careful to multiple the matrices in the correct order. This is A’B’C’D’.

2. 4 Modeling Motion in Matrices Suppose square ABCD has vertices A(-1, 2), B(-4, 1), C(-3, -2), and D(0, -1). Find the image of the square after a reflection over the y-axis. Then graph the pre-image ABCD and the image A’B’C’D’.

2. 4 Modeling Motion in Matrices There are three basic rotations about the origin for a figure.

2. 4 Modeling Motion in Matrices Suppose triangle PQR has vertices P(3, 2), Q(-1, 4), and R(1, -2). Find the image of the triangle after a rotation of 270° counterclockwise about the origin. First, write the vertices of the square as matrix.

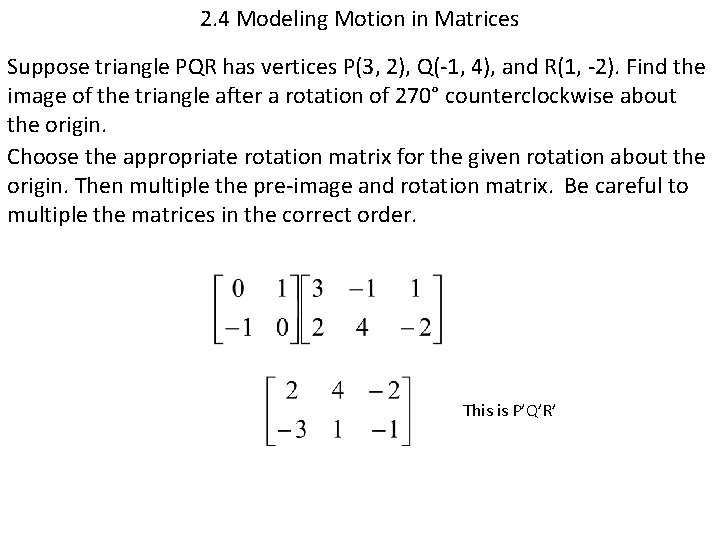
2. 4 Modeling Motion in Matrices Suppose triangle PQR has vertices P(3, 2), Q(-1, 4), and R(1, -2). Find the image of the triangle after a rotation of 270° counterclockwise about the origin. Choose the appropriate rotation matrix for the given rotation about the origin. Then multiple the pre-image and rotation matrix. Be careful to multiple the matrices in the correct order. This is P’Q’R’

2. 4 Modeling Motion in Matrices Suppose triangle PQR has vertices P(3, 2), Q(-1, 4), and R(1, -2). Find the image of the triangle after a rotation of 270° counterclockwise about the origin. Then graph the pre-image triangle PQR and the image triangle P’Q’R’.

Date Assignment number 93 -94 11 -25 odd, 26 9 Read pages 98 -101 for tomorrow.