2 4 Irreducible Matrices Reducible is reducible if

2. 4 Irreducible Matrices

Reducible is reducible if there is a permutation P such that where A 11 and A 22 are square matrices each of size at least one; otherwise A is called irreducible.

1 x 1 matrix: irr or reducible By definition, every 1 x 1 matrix is irreducible. Some authors refer to irreducible if a≠ 0 reducible if a=0
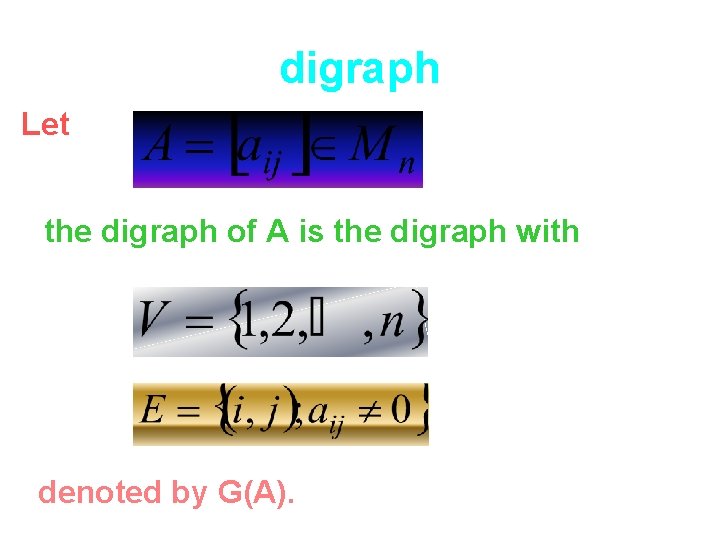
digraph Let the digraph of A is the digraph with denoted by G(A).
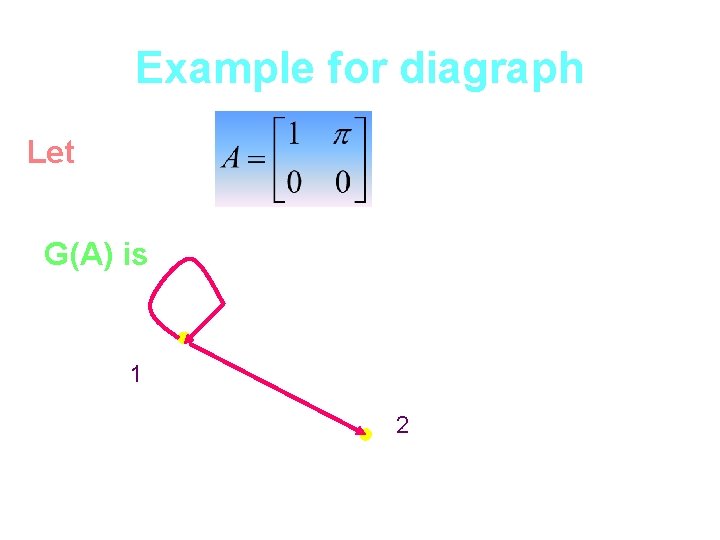
Example for diagraph Let G(A) is 1 2

strongly connected A digraph is called strongly connected if any vertices x, y, there is a directed path from x to y , and vice versa.
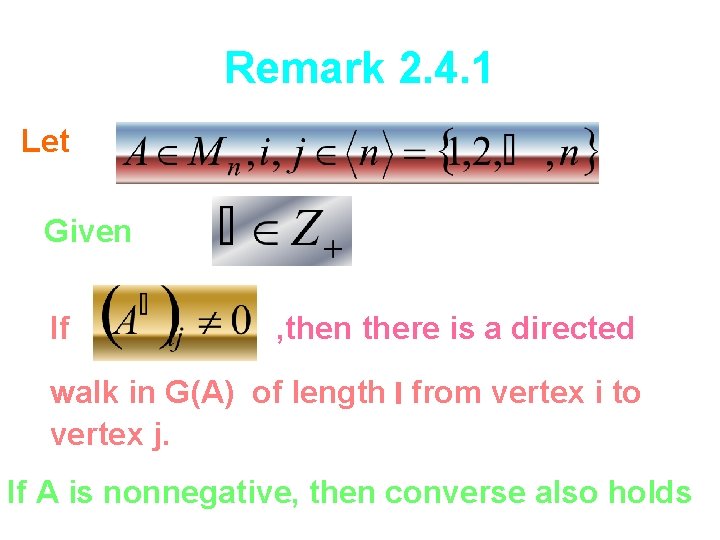
Remark 2. 4. 1 Let Given If , then there is a directed walk in G(A) of length l from vertex i to vertex j. If A is nonnegative, then converse also holds


An Equivalent relation on V Define a relation ~ on V by i~j if i=j or i≠j and there is a directed walk from vertex i to vertex j and vice versa. ~ is an equivalent relation.

Strongly Connected Component The strongly connected components are precisely the subgraphs induced by vertices that belong to a equivalent class.
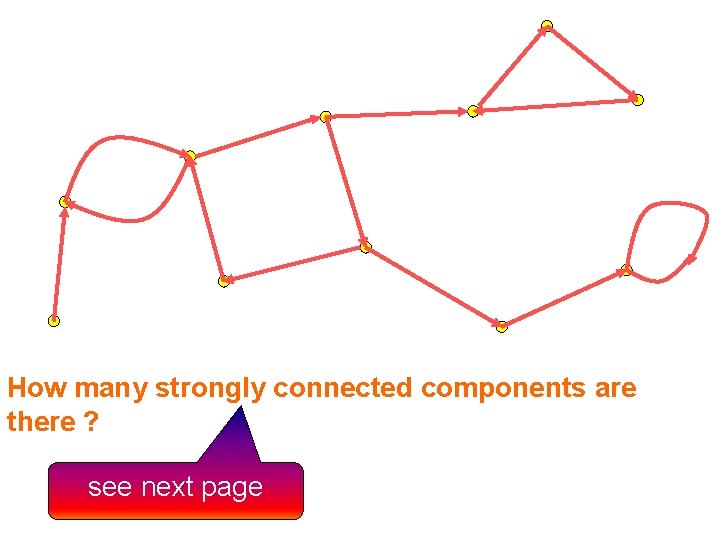
How many strongly connected components are there ? see next page
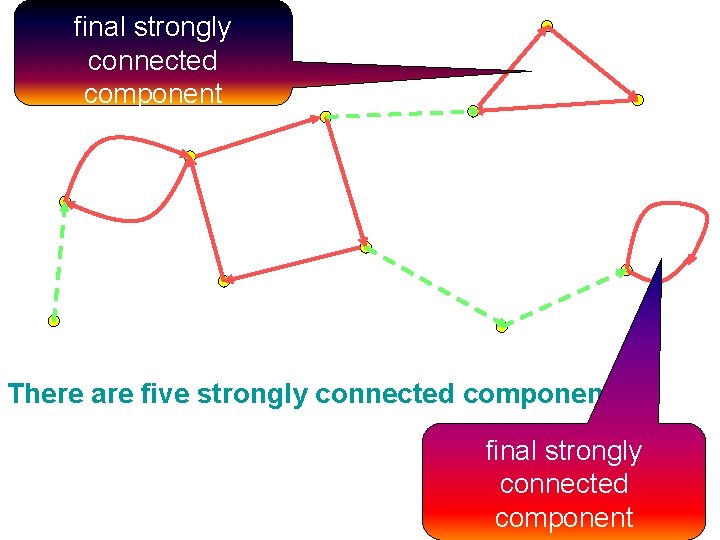
final strongly connected component There are five strongly connected components. final strongly connected component

Theorem 2. 4. 2 Let The following conditions are equivalent: (a) A is irreducible. (b) There does not exist a nonempty proper subset I of <n> such that (c) The graph G(A) is strongly connected.





Exercise 2. 4. 3 p. 1 (a) Show that a square matrix A is reducible if and only if there exists a permutation such that where A 11, A 22 are square matrices each of size at least one.



Exercise 2. 4. 3 p. 2 (b) Deduce that if A is reducible, then so is AT


Theorem 2. 4. 4 Let The following conditions are equivalent: (a) A is irreducible. (b) A has no eigenvector which is semipositive but not positive. i. e. every semipositive eigenvector of A is positive (c)






Remark If the degree of minimal polynomial of is m, then


Theorem 2. 4. 5 Let A is irreducible if and only if where m is the degree of minimal polynomial of A.


Exercise 2. 4. 6 Let A is irreducible if and only if for any semipositive vector x, if then x>0



Theorem 2. 2. 1 (Perron’s Thm) (a) (b) (c) p. 1

(d) (e) (f) A has no nonnegative eigenvector other than (multiples of) u. (g)

Theorem 2. 3. 5 (Perron-Frobenius Thm) If and , then

Corollary 2. 4. 7 Let If A is irreducible, then the conclusions (a), (b), (c), (d) and (f) of Perron Thm all hold.





Exercisse 2. 4. 8 Let Prove that if u is positive and y is nonzero then there is a unique real scalar c such that u+cy is semipositive but not positive.

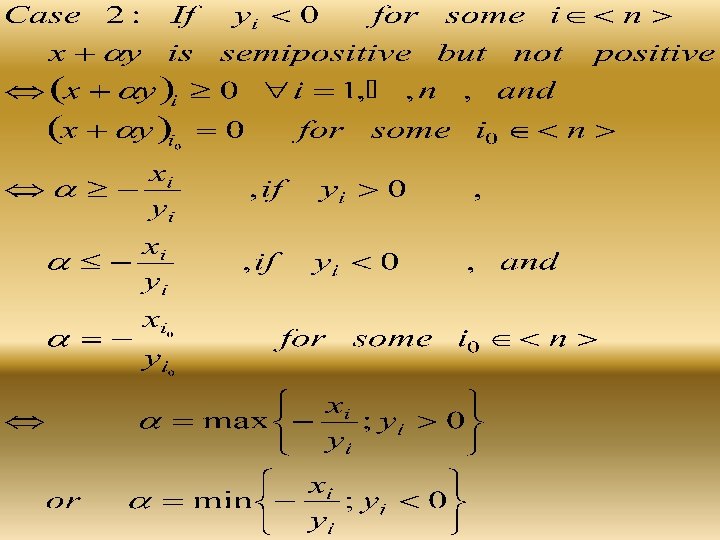

Remark 2. 4. 9 If A is nonnegative irreducible matrix and if x is nonzero nonnegative vector such that , then x must be the Perron vector of A.


Exercise 2. 4. 10 Show that the nxn permutation matrix with 1’s in positions (1, 2), (2, 3), …, (n-1, n) and (n, 1) is irreducible.


Exercise 2. 4. 11 (a) In below A and B denote arbitrary nxn nonnegative matrices. Prove or disprove the following statements: (a) If A is irreducdible, then AT is (b) irreducdible



Exercise 2. 4. 11 (b) If A is irreducible and p is a positive integer, then Ap is irreducible.



Exercise 2. 4. 11 (c) If Ap is irreducible for some positive integer, then A is irreducible.
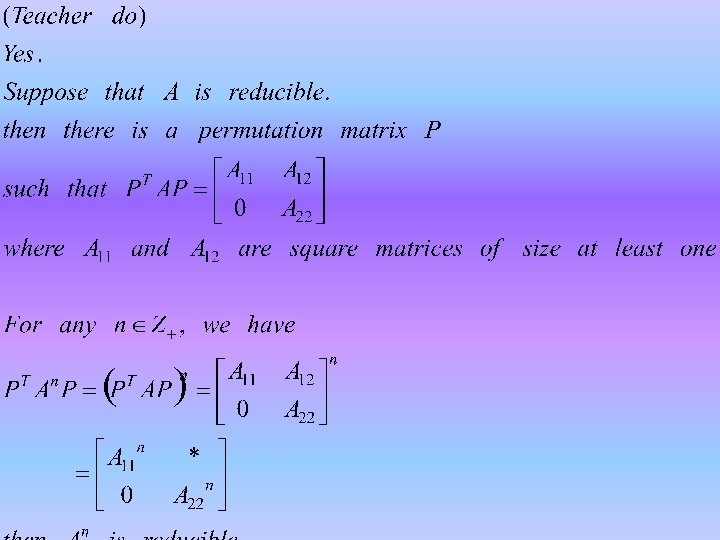


Exercise 2. 4. 11 (d) (c) If A and B are irreducible, then A+B is irreducible.

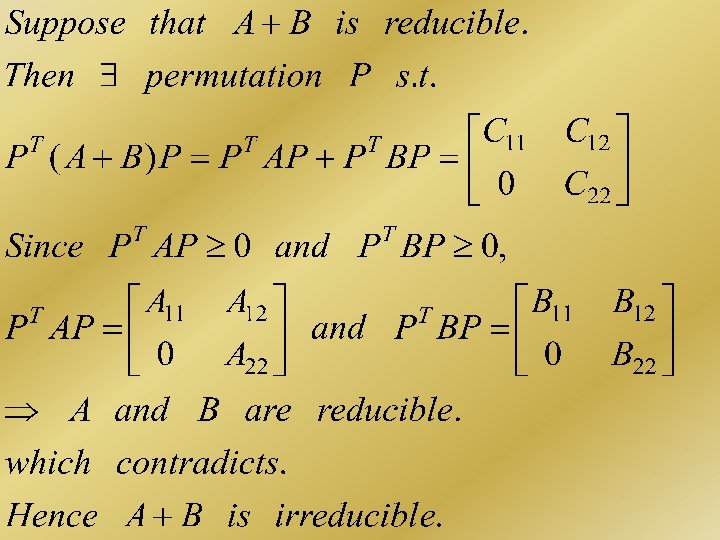

Exercise 2. 4. 11 (e) If A and B are irreducible, then AB is irreducible.



Exercise 2. 4. 11 (f) If all eigenvalues of A are 0, then A is reducible.


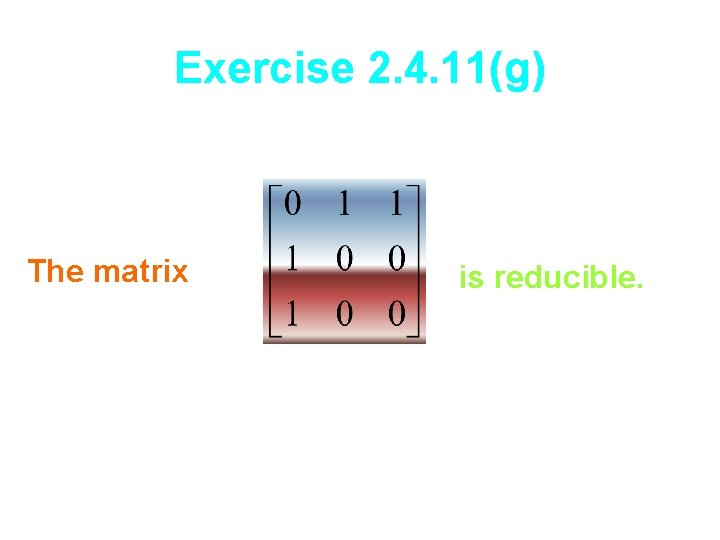
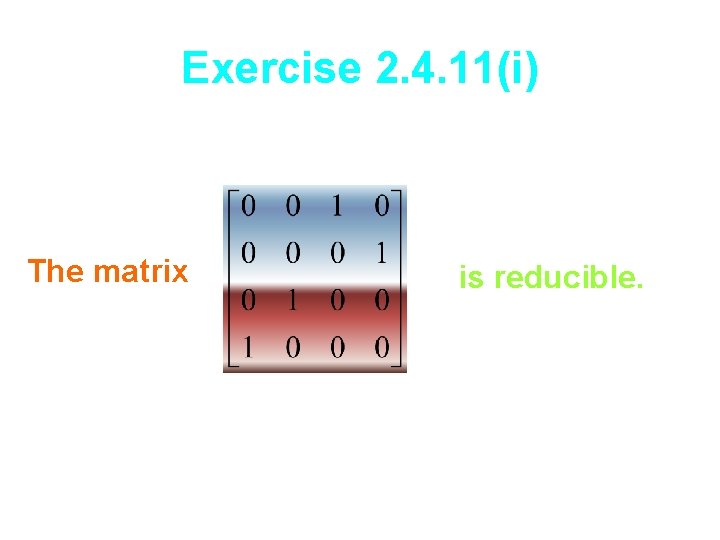
Exercise 2. 4. 11(g) The matrix is reducible.
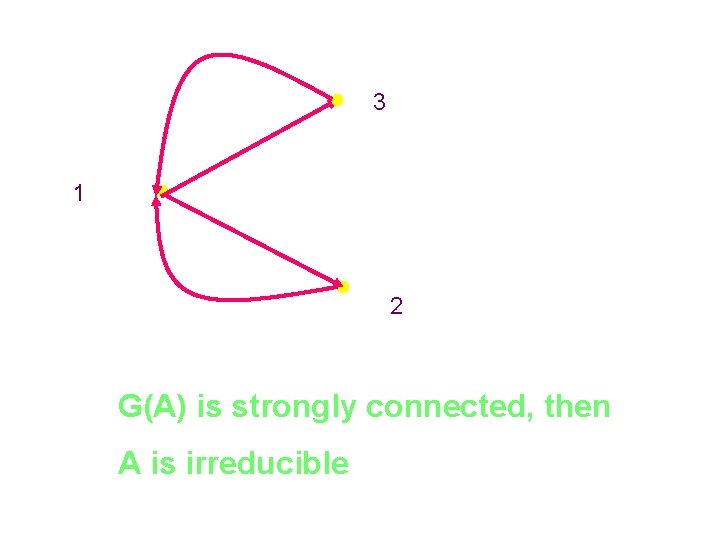
3 1 2 G(A) is strongly connected, then A is irreducible
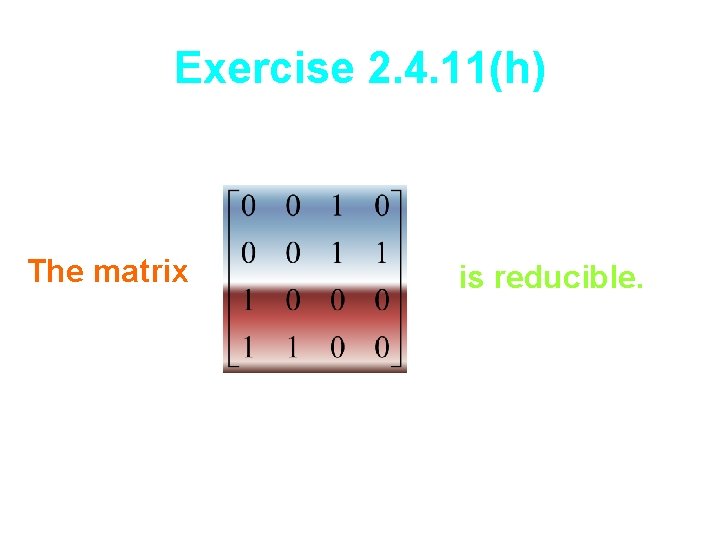
Exercise 2. 4. 11(h) The matrix is reducible.
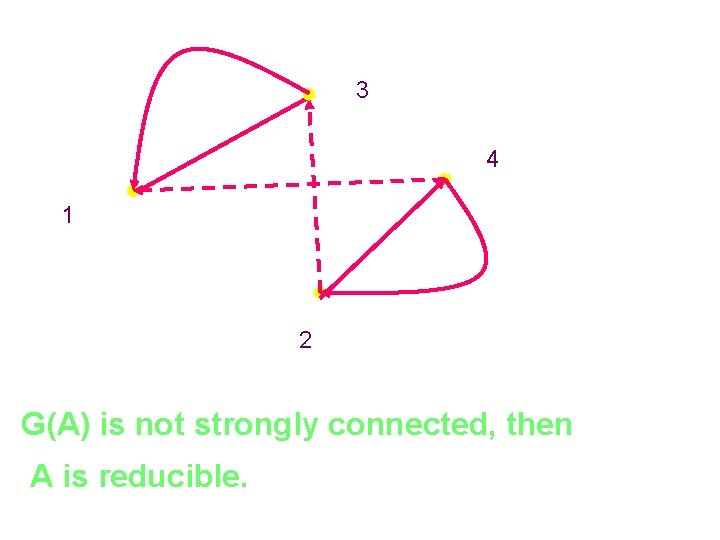
3 4 1 2 G(A) is not strongly connected, then A is reducible.
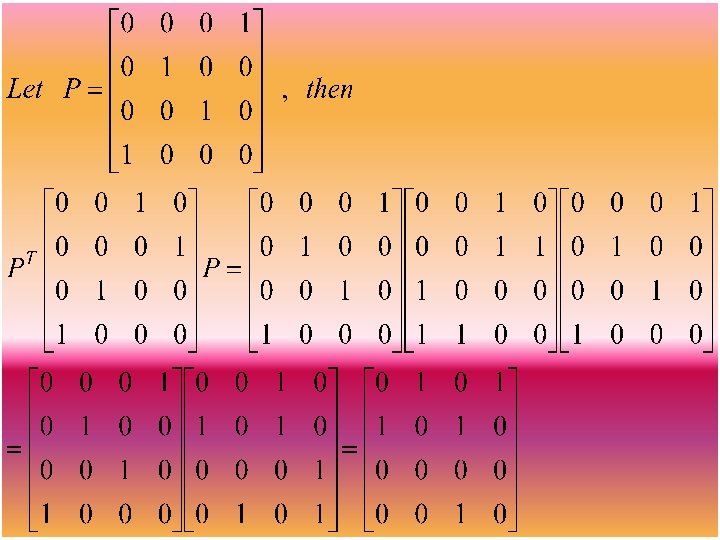
Exercise 2. 4. 11(i) The matrix is reducible.
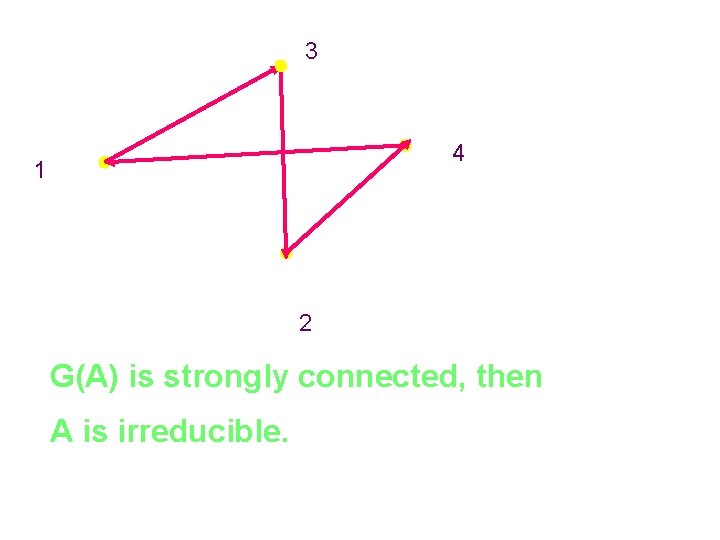
3 4 1 2 G(A) is strongly connected, then A is irreducible.

Exercisse 2. 4. 11(j) A is irreducible if and only if is irreducible.





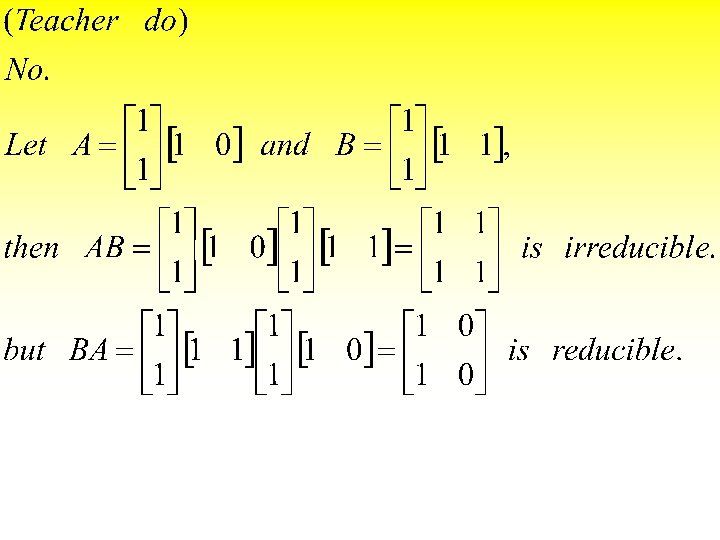
Exercisse 2. 4. 11(k) If AB is irreducible, then BA is irreducible


Exercise 2. 4. 12. Let A be an nxn irreducible nonnegative matrix. Prove that if then all row sums of A are equal. Give an example to show that the result no longer holds if the irreducibility assumption is removed.
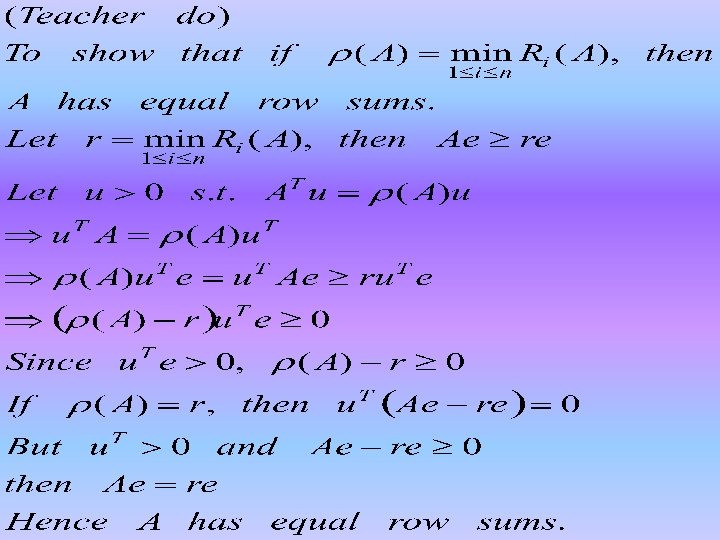
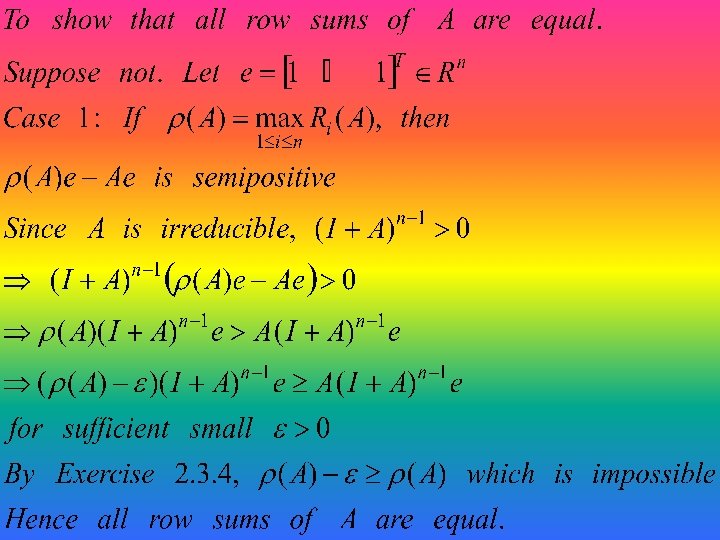



- Slides: 89