2 4 Building a System of Geometry Knowledge

2. 4 Building a System of Geometry Knowledge Obj: Identify Properties to use in Proofs

Algebraic Properties of Equality Let a, b, and c be real numbers or expressions representing real numbers Addition prop: if a=b, then a+c=b+c Subtraction Prop if a=b, then a-c=b-c Multiplication Prop: if a=b, then ac=bc Division Prop: if a=b and c not equal 0, then a/c=b/c Substitution Prop: if a=b, you may replace a with b in any true equation containing and the resulting equation will still be true. * You can perform the same operation to both side of an equation and the equality will still hold

Example of use of Algebraic Properties Solve the equation and justify each step 2 x + 6 = 24

Equivalence Properties of Equality Reflexive Prop: for any real number a, a=a Symmetric Prop: For all real numbers a and b, if a=b, then b=a Transitive Prop: For all real numbers a, b, and c, if a=b and b=c, then a=c.

Equivalence Properties of Congruence Reflexive Prop: figure A Symmetric Prop: if figure A Transitive Prop: If figure A then figure A figure C figure A figure B, then figure B, and figure B figure A figure C,

Two- Column Proof l A proof in which the statements are written in the lefthand column and the reasons are given in the righthand column.

How to Prove a Theorem l Include the following parts – – – Given (hypothesis of theorem) Prove (Conclusion of theorem) Picture 2 columns of statements and reasons Conclusion

How long is AC? How long is BD? What is true about AC and BD? Why?

*First think through before writing!!! Ex: Given AB = CD. Prove that AC=BD Statement Reasons A B C D

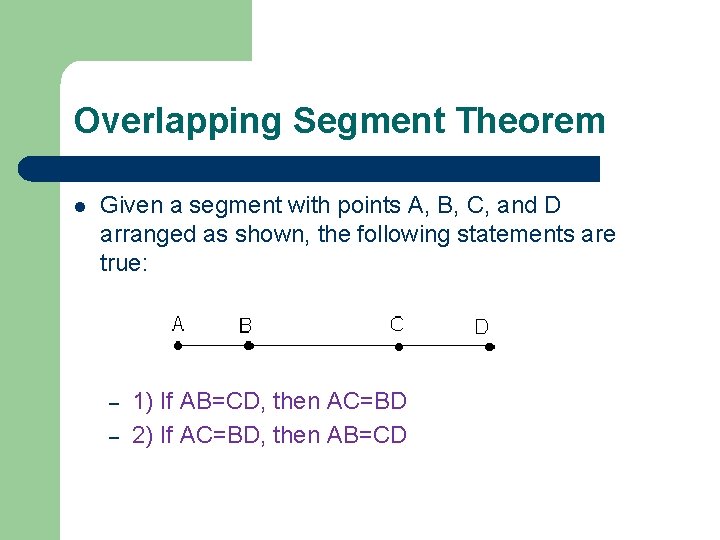
Overlapping Segment Theorem l Given a segment with points A, B, C, and D arranged as shown, the following statements are true: – – 1) If AB=CD, then AC=BD 2) If AC=BD, then AB=CD

Overlapping Angle Theorem l Given <AOD with pts. B and C in its interior, the following statements are true: – – 1) If m<AOB=m<COD, then m<AOC=m<BOD 2) if m<AOC=m<BOD, then m<AOB=m<COD

Practice: Fill in the missing pieces of the proof for the 2 nd part of the overlapping segment theorem Given: ______ Prove: AB = CD Statements Picture: Reasons l AC = BD 1) _________ l _________ 2) Segment Addition Postulate l _________ 3) Segment Addition Postulate l AB + BC = CD + BC 4) ___________ l AB = CD 5) ___________

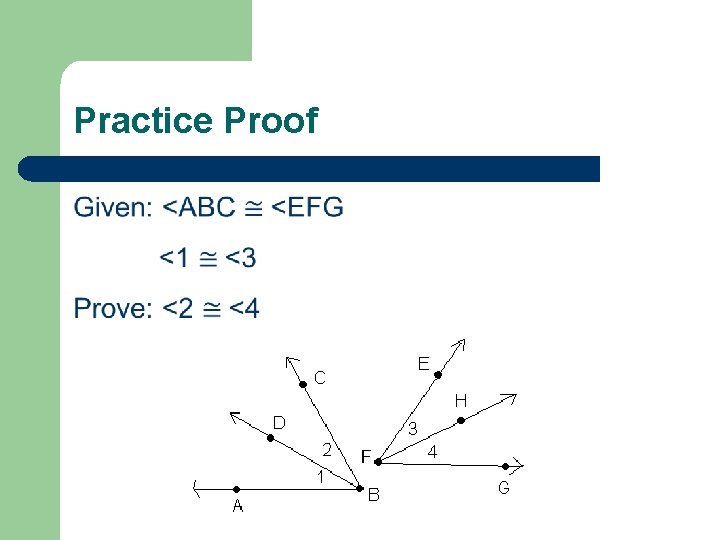
Practice Proof

Statement Reason