2 4 An Introduction to Problem Solving Strategy

§ 2. 4 An Introduction to Problem Solving

Strategy for Problem Solving General Strategy for Problem Solving 1) 2) 3) 4) UNDERSTAND the problem. • Read and reread the problem. • Choose a variable to represent the unknown. • Construct a drawing, whenever possible. • Propose a solution and check. TRANSLATE the problem into an equation. SOLVE the equation. INTERPRET the result. • Check the proposed solution in the problem. • State your conclusion. Martin-Gay, Beginning and Intermediate Algebra, 4 ed 2

Finding an Unknown Number Example: The product of twice a number and three is the same as the sum of five times the number and 12. Find the number. 1. ) UNDERSTAND Read and reread the problem. If we let x = the unknown number, then “twice a number” translates to 2 x, “the product of twice a number and three” translates to 2 x · 3, “five times the number” translates to 5 x, and “the sum of five times the number and 12” translates to 5 x + 12. Continued Martin-Gay, Beginning and Intermediate Algebra, 4 ed 3
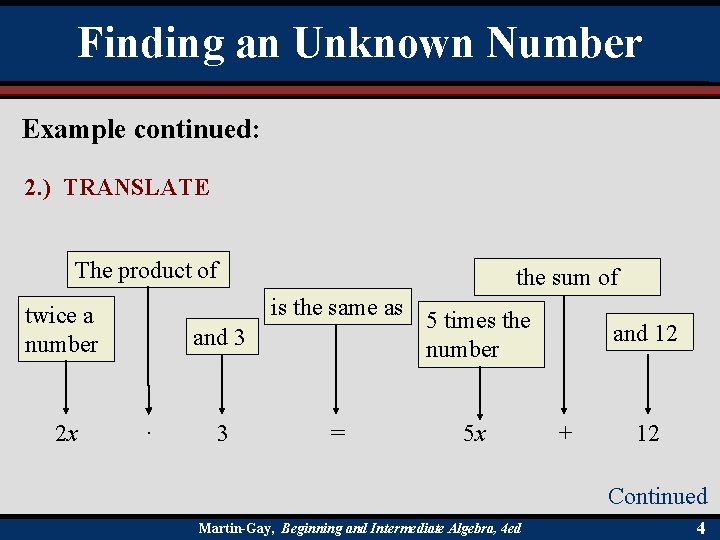
Finding an Unknown Number Example continued: 2. ) TRANSLATE The product of is the same as twice a number 2 x the sum of and 3 · 3 = 5 times the number 5 x and 12 + 12 Continued Martin-Gay, Beginning and Intermediate Algebra, 4 ed 4

Finding an Unknown Number Example continued: 3. ) SOLVE 2 x · 3 = 5 x + 12 6 x = 5 x + 12 Simplify left side. 6 x + (– 5 x) = 5 x + (– 5 x) + 12 Add – 5 x to both sides. x = 12 Simplify both sides. 4. ) INTERPRET Check: Replace “number” in the original statement of the problem with 12. The product of twice 12 and 3 is 2(12)(3) = 72. The sum of five times 12 and 12 is 5(12) + 12 = 72. We get the same results for both portions. State: The number is 12. Martin-Gay, Beginning and Intermediate Algebra, 4 ed 5

Solving a Problem Example: A car rental agency advertised renting a Buick Century for $24. 95 per day and $0. 29 per mile. If you rent this car for 2 days, how many whole miles can you drive on a $100 budget? 1. ) UNDERSTAND Read and reread the problem. Let’s propose that we drive a total of 100 miles over the 2 days. Then we need to take twice the daily rate and add the fee for mileage to get 2(24. 95) + 0. 29(100) = 49. 90 + 29 = 78. 90. This gives us an idea of how the cost is calculated, and also know that the number of miles will be greater than 100. If we let x = the number of whole miles driven, then 0. 29 x = the cost for mileage driven Martin-Gay, Beginning and Intermediate Algebra, 4 ed Continued 6

Solving a Problem Example continued: 2. ) TRANSLATE Daily costs mileage costs plus 2(24. 95) + maximum budget is equal to 0. 29 x = 100 Continued Martin-Gay, Beginning and Intermediate Algebra, 4 ed 7

Solving a Problem Example continued: 3. ) SOLVE 2(24. 95) + 0. 29 x = 100 49. 90 + 0. 29 x = 100 Simplify left side. 49. 90 – 49. 90 + 0. 29 x = 100 – 49. 90 Subtract 49. 90 from both sides. 0. 29 x = 50. 10 Simplify both sides. Divide both sides by 0. 29. x 172. 75 Simplify both sides. Martin-Gay, Beginning and Intermediate Algebra, 4 ed Continued 8

Solving a Problem Example continued: 4. ) INTERPRET Check: Recall that the original statement of the problem asked for a “whole number” of miles. If we replace “number of miles” in the problem with 173, then 49. 90 + 0. 29(173) = 100. 07, which is over our budget. However, 49. 90 + 0. 29(172) = 99. 78, which is within the budget. State: The maximum number of whole number miles is 172. Martin-Gay, Beginning and Intermediate Algebra, 4 ed 9
- Slides: 9