2 4 5 10 12 Simplify Simplifying Radical
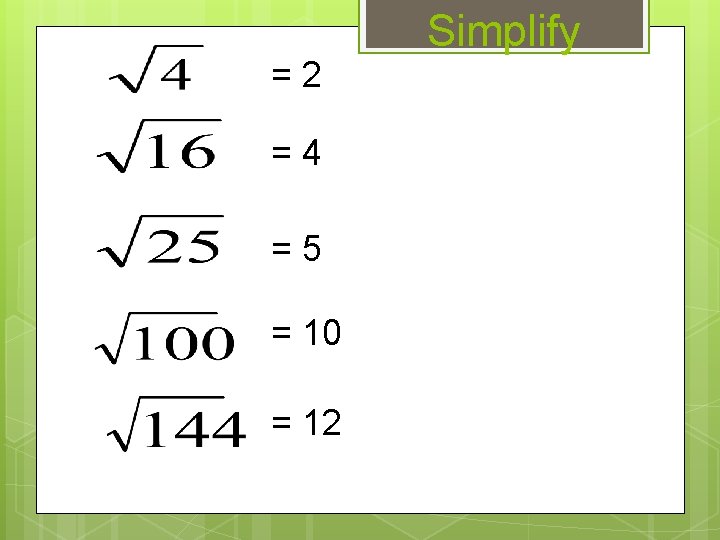









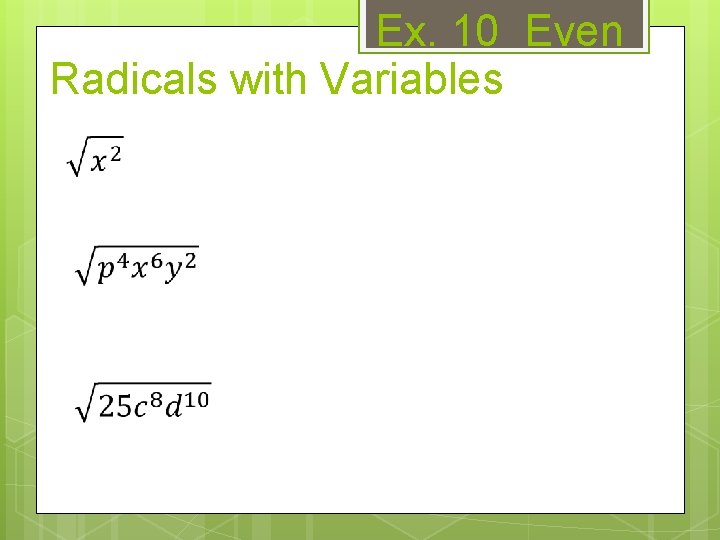







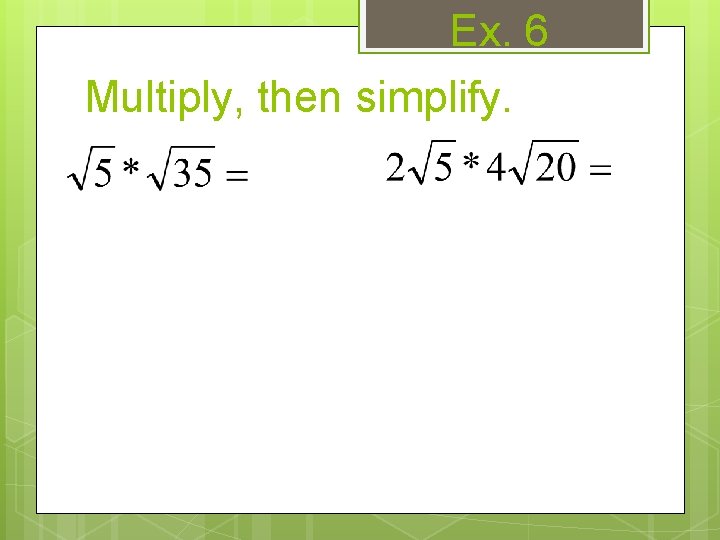


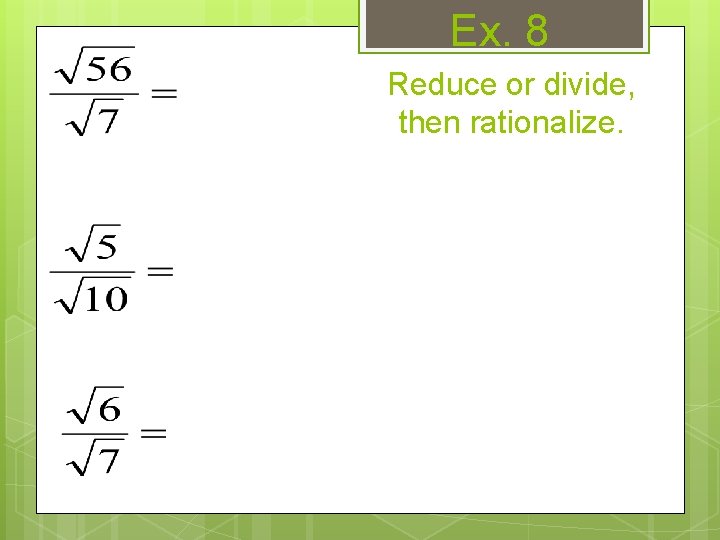

- Slides: 25
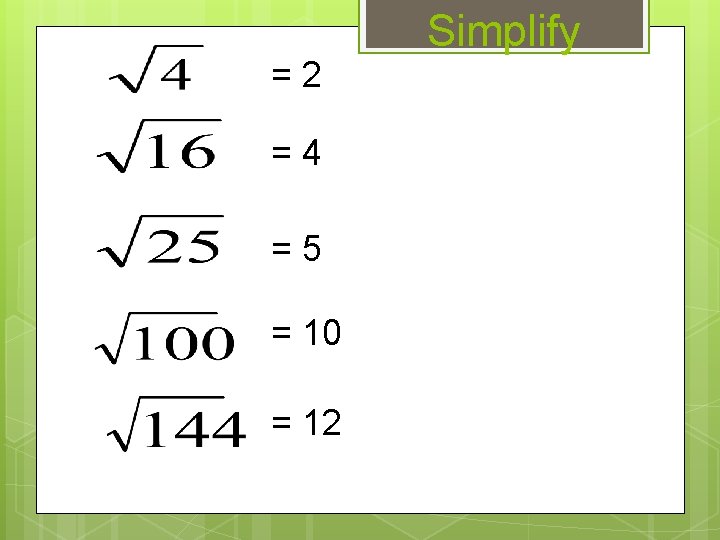
=2 =4 =5 = 10 = 12 Simplify

Simplifying Radical Expressions A radical expression is in its simplified form if it contains no perfect squares as factors.

Objective - To simplify rational and irrational square roots. List of Perfect Squares

Objective - To simplify irrational roots. Example: Check using a calculator!

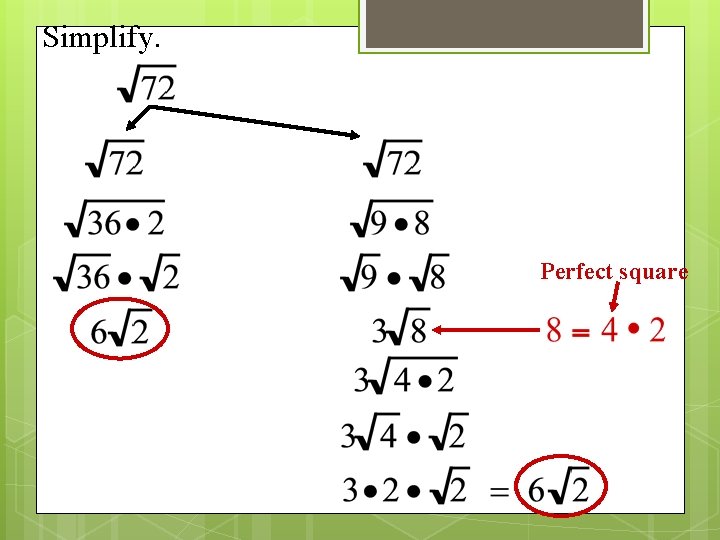
Simplify. To simplify the number by hand must have a perfect square factor. Can’t be simplified No perfect square factors

Simplify each irrational root. 1) 4) 2) 5) 3) 6)

Simplify. Perfect square

Simplify each irrational root. 1) 4) Already Simplified 2) 5) 3) 6)

Ex. 1 Simplify

Ex. 2 Simplify

Radicals with Variables To simplify radicals with variables: divide even exponents by 2; for odd exponents, pull out the largest even exponent, take the square root of that, and leave the remainder under the radical.
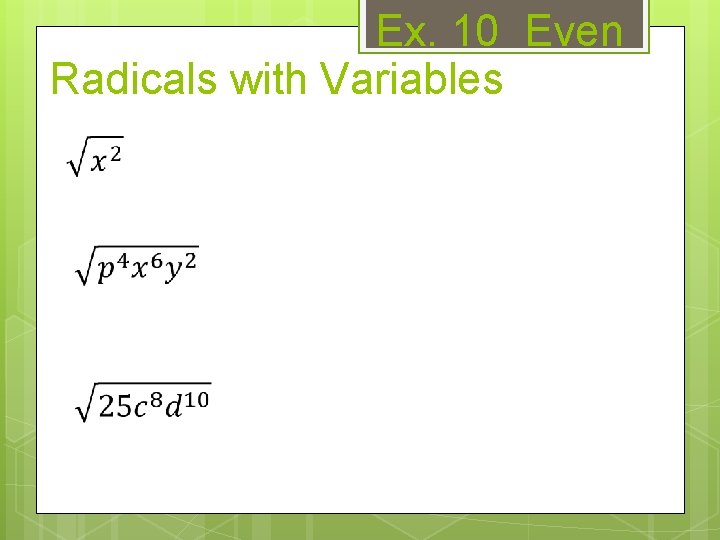
Ex. 10 Even Radicals with Variables

Ex. 11 Odd Radicals with Variables

Combine Like Radicals Miller + Miller To combine radicals: combine the coefficients of like radicals. They must have the same last name.

Ex. 3 Simplify Your Turn

Ex. 4 Simplify, then combine.

Ex. 5 Simplify, then combine.

Slide 10 - 18 Example The greatest perfect square factor of 96 a 4 b is 16 a 4. Use the product rule of square roots to separate the factors into two radicals. Find the square root of 16 a 4 and leave 6 b in the radical. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

Slide 10 - 19 Example Solution The greatest perfect square factor of 32 x 5 is 16 x 4. Use the product rule of square roots to separate the factors into two radicals. Find the square root of 16 x 4 and leave 2 x in the radical.

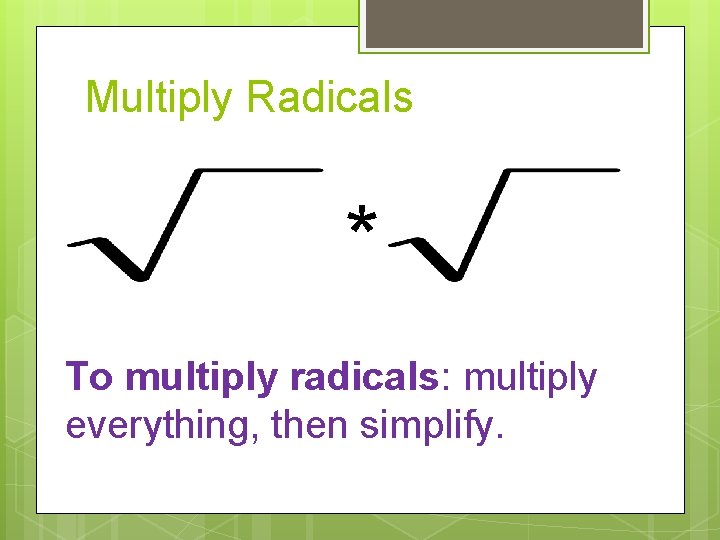
Multiply Radicals * To multiply radicals: multiply everything, then simplify.
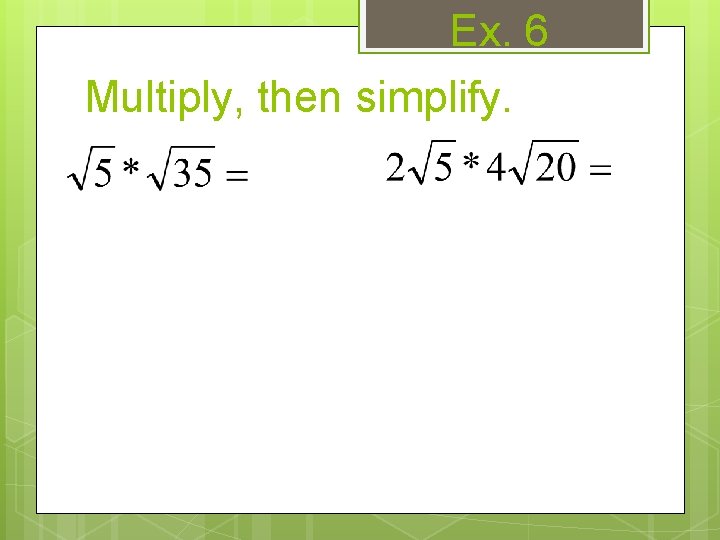
Ex. 6 Multiply, then simplify.

Ex. 7 Squared and Square Root Cancel

Dividing Radicals To divide radicals: reduce or divide what you can and rationalize the denominator. A square root CANNOT be in the denominator.
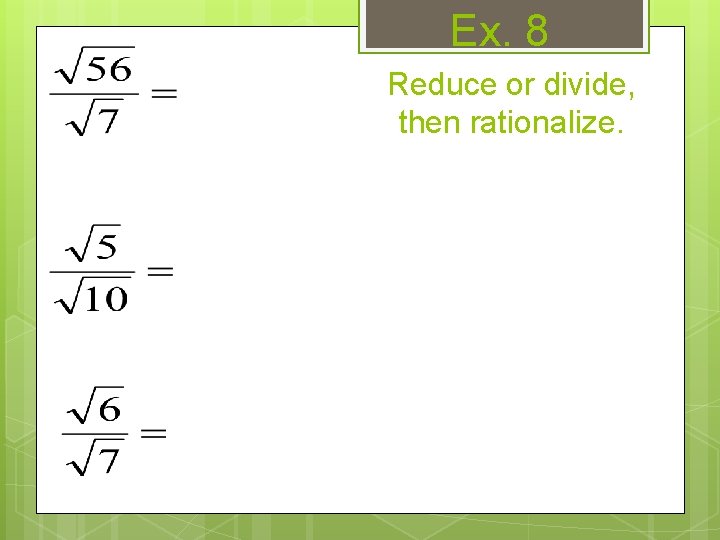
Ex. 8 Reduce or divide, then rationalize.

Ex. 9