2 3 Solving Linear Equations Groups Section 2



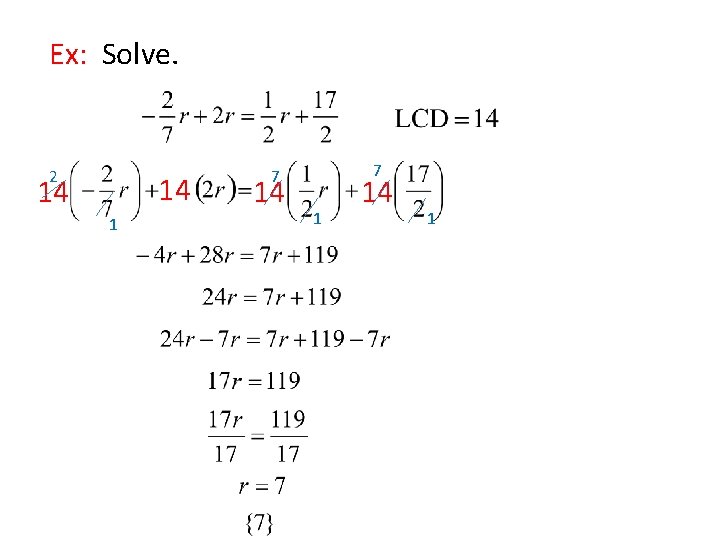
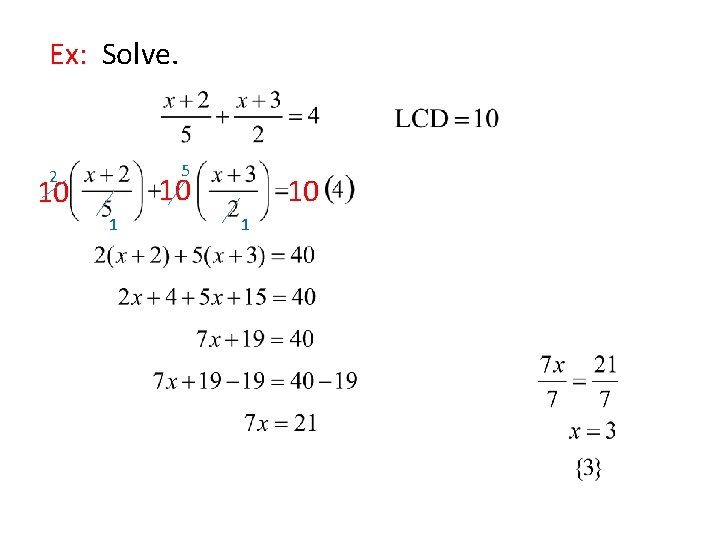


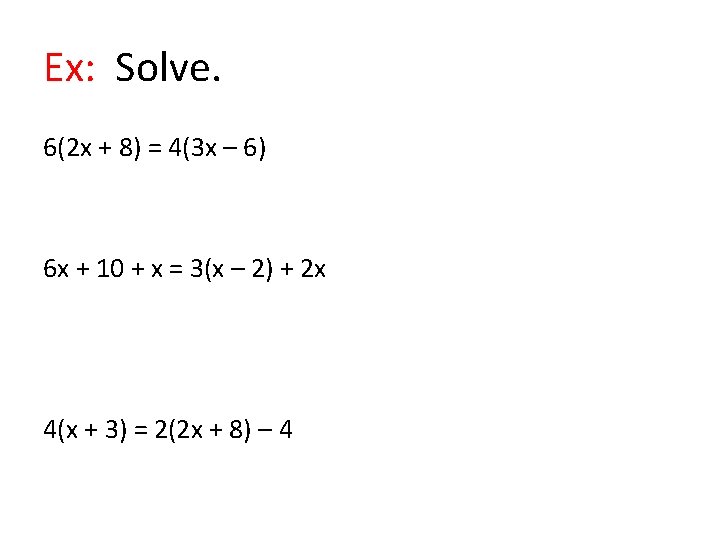



- Slides: 11

2. 3 Solving Linear Equations

Groups • Section 2. 2 Pg 122: 15, 53, 62, 77 • Section 2. 3 Page 132: 1, 23, 29

Clearing Fractions Multiply EVERY term on each side of the eqn. by the LCD.
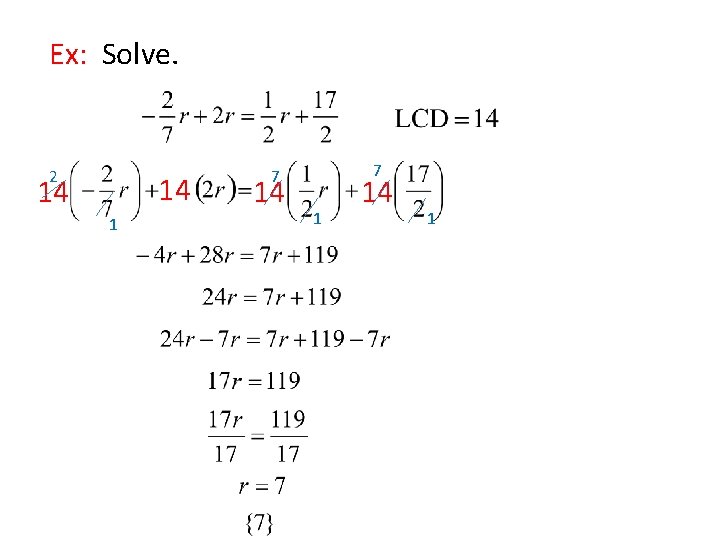
Ex: Solve. 2 14 14 1 7 7 14 1
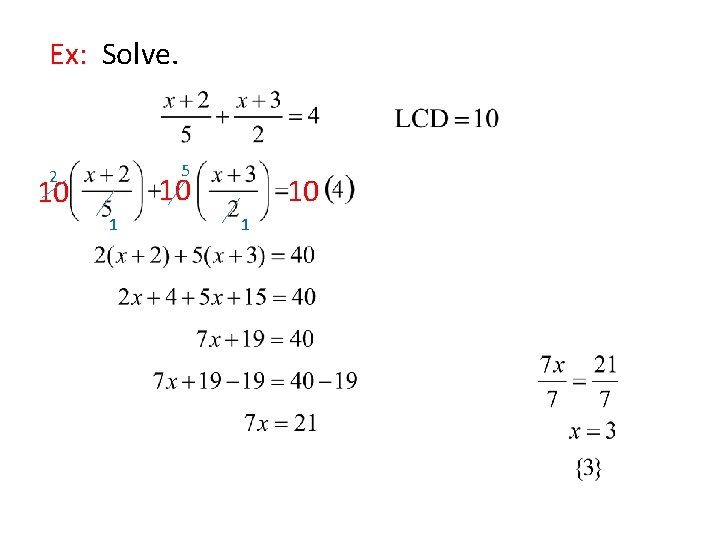
Ex: Solve. 5 2 10 10 1

Steps for Solving a Linear Eqn 1. Use dist. prop. to eliminate ( ) a. Clear fractions by mult. every term by LCD b. Simplify each side of eqn. 2. Use add. prop. of equality to get all variable terms on one side of eqn and all constants on other side 3. Use mult. prop. of equality to get the coefficient of the variable to be 1 (like x or 1 x) 4. Check soln. in original eqn (if necessary)

Types of Equations Answer: 1. Conditional Eqn– has (at least) one solution, but not infinitely many 2. Identity – infinitely many solutions (all real #s are solns) 3. Inconsistent Eqn – no soln x= {x|x is a real number} “No solution” or ø
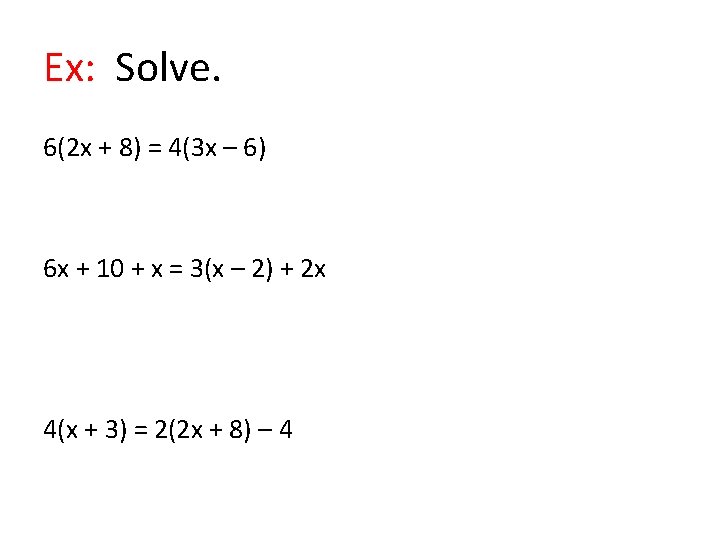
Ex: Solve. 6(2 x + 8) = 4(3 x – 6) 6 x + 10 + x = 3(x – 2) + 2 x 4(x + 3) = 2(2 x + 8) – 4

Ex: Solve. 6(2 x + 8) = 4(3 x – 6) 6(2 x) + 6(8) = 4(3 x) – 4(6) 12 x + 48 = 12 x – 24 12 x + 48 – 12 x = 12 x – 24 – 12 x 48 = -24 No Variables remain & stmt is false -> inconsistent eqn. (so there is NO solution) Ans: ø

Ex: Solve. 6 x + 10 + x = 3(x – 2) + 2 x 6 x + 10 + x = 3(x) – 3(2) + 2 x 7 x + 10 = 3 x – 6 + 2 x 7 x + 10 = 5 x – 6 7 x – 5 x + 10 = -6 – 5 x 2 x + 10 = -6 2 x + 10 – 10 = -6 – 10 2 x = -16 2 2 x = -8 {-8} • Distribute • Combine like terms • Add. Prop of equality • Add. Prop. of equality • Mult. Prop. Of equality Conditional Eqn.

Ex: Solve. 4(x + 3) = 2(2 x + 8) – 4 4(x) + 4(3) = 2(2 x) + 2(8) – 4 4 x + 12 = 4 x + 16 – 4 4 x + 12 = 4 x + 12 – 4 x 12 = 12 No Variables remain & stmt is true -> identity (so all real #s are solutions) Ans: {x|x is a real number}