2 3 Modeling Real World Data with Matrices

2. 3 Modeling Real World Data with Matrices Objectives: Model data using matrices. Add, subtract, and multiply matrices.

Matrix: A rectangular array of terms called elements. Dimensions: In a matrix they are m x n matrix: A matrix with m rows and n columns. “m by n” Row matrix: A matrix with only one row. Column matrix: A matrix with only one column. Square matrix: A matrix with the same number of rows as columns.

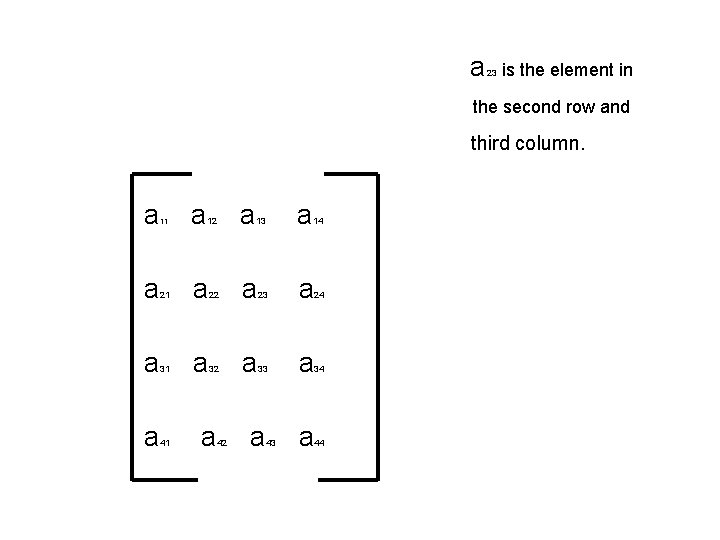
a 23 is the element in the second row and third column. a 11 a 12 a 13 a 14 a 21 a 22 a 23 a 24 a 31 a 32 a 33 a 34 a 41 a a 44 a 42 43

Ex. 1 During the summer of 2000, Ms. Robbins received several types of grains on her farm to feed her livestock. a. ) Use a matrix to represent the data. June – 15, 000 bushels of corn - 2, 000 bushels of soybeans - 500 bushels of oats July – 13, 500 bushels of corn - 6, 500 bushels of soybeans - 1, 000 bushels of oats Aug. - 14, 000 bushels of corn - 5, 500 bushels of soybeans - 1500 bushels of oats. b) Use a symbol to represent the number of bushels of soybeans in August.

Equal Matrices: Two matrices are equal iff they have the same dimensions and are identical, element by element. Ex. 2) Find the values of x and y for which the matrix equation is: y 4 x y– 3 2 x + 1 Addition of Matrices: The sum of two m x n matrices is an m x n matrix in which the elements are the sum of the corresponding elements of the given matrices.

Ex. 3) Find A + B if A= -7 4 and B = 6 10 5 0 8 -9 3 -1 -2 5 Subtraction The difference A – B of two m x n matrices is equal to the sum of A + (-B), where –B of Matrices: represents the additive inverse of B. Ex. 4) Find S - T if S = 2 -1 3 -4 -2 -8 and T = -5 -4 1 7 -8 4

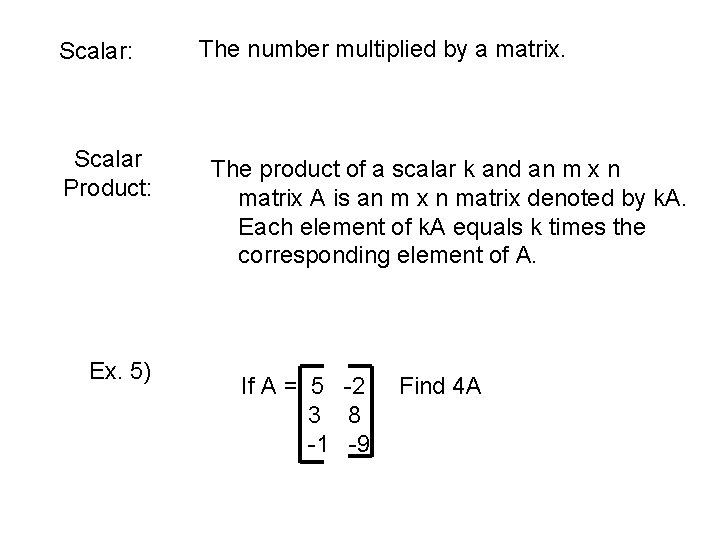
Scalar: Scalar Product: Ex. 5) The number multiplied by a matrix. The product of a scalar k and an m x n matrix A is an m x n matrix denoted by k. A. Each element of k. A equals k times the corresponding element of A. If A = 5 -2 3 8 -1 -9 Find 4 A

Product of Two Matrices: The product of an m x n matrix A and an n x r matrix B is an m x r matrix AB. The ijth element of AB is the sum of the products of the corresponding elements in the ith row of A and the jth column of B. *Can only multiply if the number of columns in A is the same as the number of rows in B.

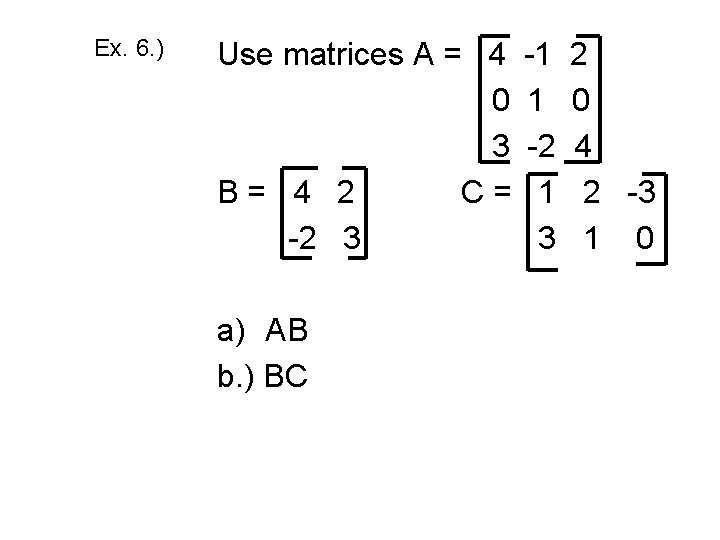
Ex. 6. ) Use matrices A = 4 0 3 B= 4 2 C= -2 3 a) AB b. ) BC -1 1 -2 1 3 2 0 4 2 -3 1 0