2 3 Continuity and Intermediate Value Theorem Continuity

2. 3 Continuity and Intermediate Value Theorem

Continuity • A function is continuous if you can draw the graph without picking up your pencil. Definition: A function y = f(x) is continuous at an interior point c in its domain if (the limit has to equal the value of the function at c)

Continuity (at endpoints) • A function y = f(x) is continuous at a left endpoint a or a right endpoint b in its domain if or If a function is not continuous anywhere on its graph, we say there is a discontinuity at that point.

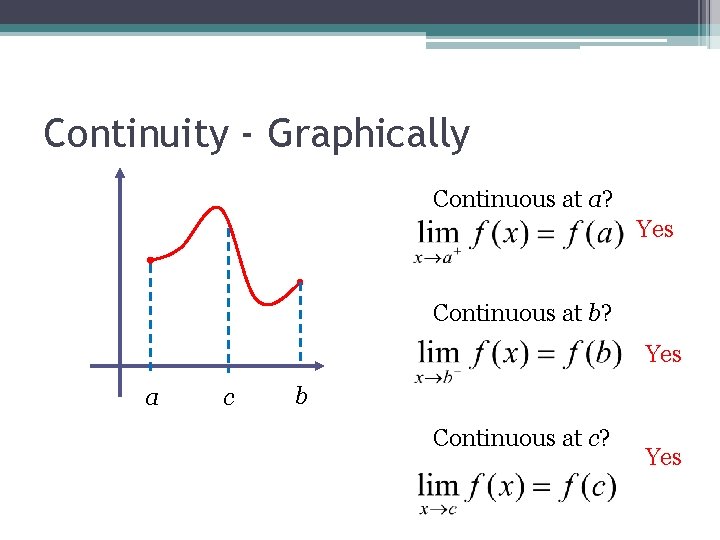
Continuity - Graphically Continuous at a? Yes Continuous at b? Yes a c b Continuous at c? Yes

Discontinuities • Is continuous for all real numbers? This is an example of a nonremovable discontinuity at x = 0. (vertical asymptote)

Discontinuities • Is f(x) = [x] continuous for all real numbers? Since the limit does not exist, we can say the function is discontinuous. This is another example of a nonremovable discontinuity at x = 0. (jump)

Discontinuities • Is the function all real numbers? continuous for Sin constantly oscillates, so we cannot say that these two limits are the same. Thus, the limit as x approaches 0 does not exist and there is a discontinuity here. Another nonremovable discontinuity. (infinite oscillation)

Discontinuities • Is continuous everywhere? (1, 2) because f(1) does not exist. This is an example of a removable discontinuity at x = 1. (hole)

Removing a Discontinuity (hole) • How can we make continuous? The only place in question is at x = 1. When you cancel out like factors in the top and bottom, this means there is a hole at where the denominator was equal to 0. To be continuous, the limit as x approaches 1 has to be the value of the function at 1. Therefore, to be continuous, f(1) = 2.

Removing a Discontinuity (hole) • How can we make continuous? We can now turn the original function into a piecewise so that f(1) not only exists, but is equal to the limit as x approaches 1, which was 2.

Properties of Continuous Functions • If two functions are continuous, then ▫ ▫ The sum of the functions is also continuous. The difference of the functions is also continuous The product of the functions is also continuous. The result of multiplying one of the functions by a constant is also continuous. ▫ The quotient of the functions is also continuous provided the denominator ≠ 0

Theorem Involving Composites • If f(x) = │x │ and g(x) = cos x, what is f(g(x))? f(g(x)) = │cos x│ If f and g are both continuous functions, the composites of two continuous functions is also always continuous.

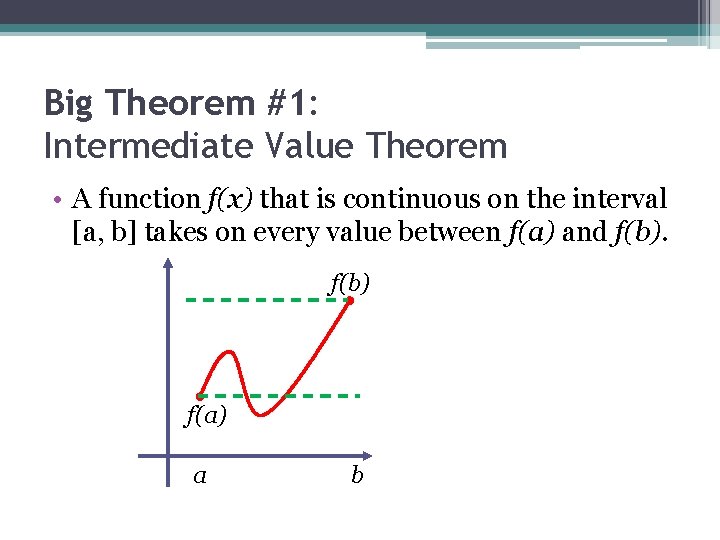
Big Theorem #1: Intermediate Value Theorem • A function f(x) that is continuous on the interval [a, b] takes on every value between f(a) and f(b) f(a) a b

Intermediate Value Theorem • Show using the IVT that has a root between x = 2 and x = 3. f(x) is discontinuous only at x = – 1, so on the interval [2, 3] the function is continuous. Since f is cont. on [2, 3] and f(2) and f(3) have opposite signs, there is a value c in the Interval where f(c) = 0 by the Intermediate Value Theorem.