2 3 C Parallel and Perpendicular Lines Objectives

2 -3 C Parallel and Perpendicular Lines Objectives: • How do you know if slopes are parallel or perpendicular? • What are skew lines?

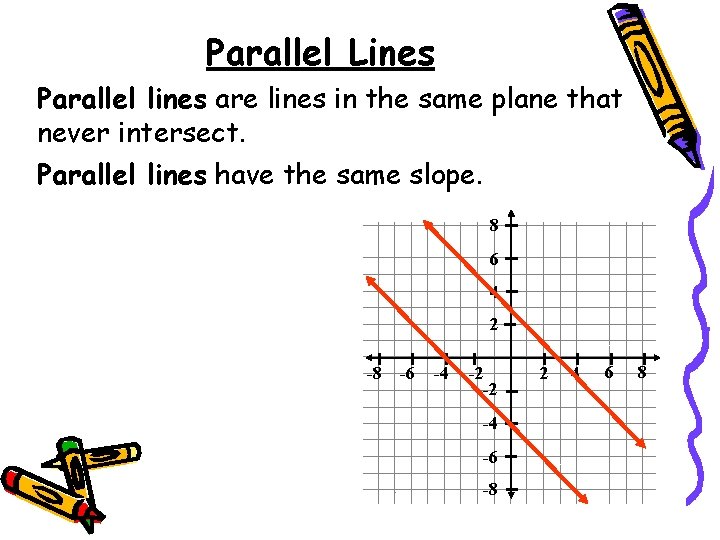
Parallel Lines Parallel lines are lines in the same plane that never intersect. Parallel lines have the same slope. 8 6 4 2 -8 -6 -4 -2 -2 -4 -6 -8 2 4 6 8

Example 1 Determine whether these lines are parallel. y = 4 x + 2 y = 4 x -6 and The slope of both lines is 4. So, the lines are parallel.

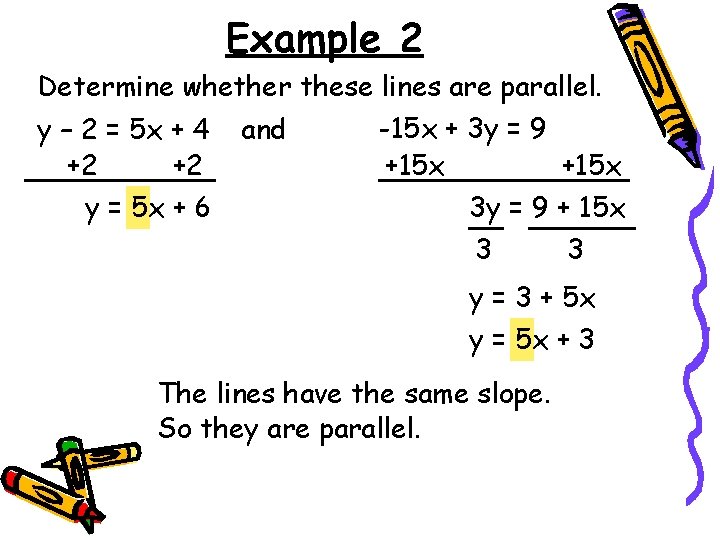
Example 2 Determine whether these lines are parallel. -15 x + 3 y = 9 y – 2 = 5 x + 4 and +2 +2 +15 x y = 5 x + 6 3 y = 9 + 15 x 3 3 y = 3 + 5 x y = 5 x + 3 The lines have the same slope. So they are parallel.

Example 3 Determine whether these lines are parallel. -5 = -2 y + 8 x y = -4 x + 2 and +2 y + 2 y 2 y - 5 = 8 x +5 +5 2 y = 8 x + 5 2 2 Since these lines have different slopes, they are not parallel.

Practice Determine whether the graphs are parallel lines. 1. no 1) y = -5 x – 8 and y = 5 x + 2 2) 3 x – y = -5 and 5 y – 15 x = 10 2. yes 3) 4 y = -12 x + 16 and y = 3 x + 4 3. no

Practice Write the slope-intercept form of the equation of the line passing through the point (0, 2) and parallel to the line 3 y – x = 0. 3 y = x Y = ⅓x m=⅓ y = ⅓x + b 2 = ⅓(0) + b 2=b y = ⅓x + 2

Practice Determine whether the graphs of the equations are parallel lines. 1) 3 x – 4 = y and y – 3 x = 8 2) y = -4 x + 2 and -5 = -2 y + 8 x 1. yes 2. no

Skew lines are noncoplanar lines. (Noncoplanar lines cannot intersect. )

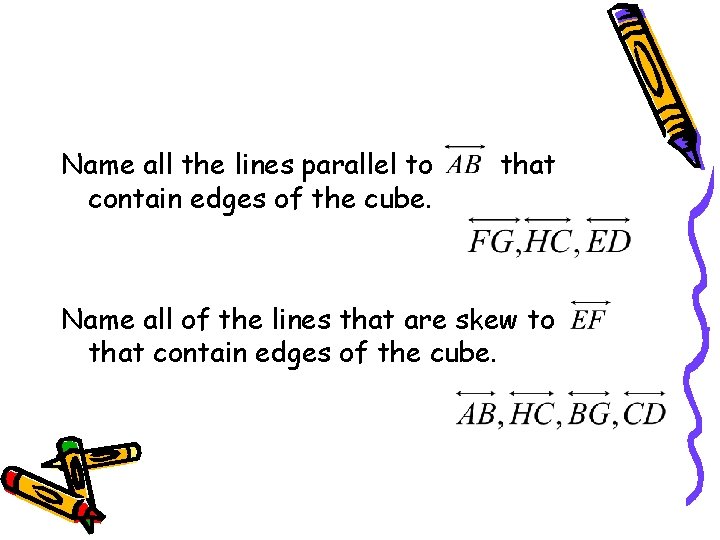
Name all the lines parallel to contain edges of the cube. that Name all of the lines that are skew to that contain edges of the cube.

2 -3 C Parallel and Perpendicular Lines Objectives: • To determine whether the graphs of two equations are perpendicular

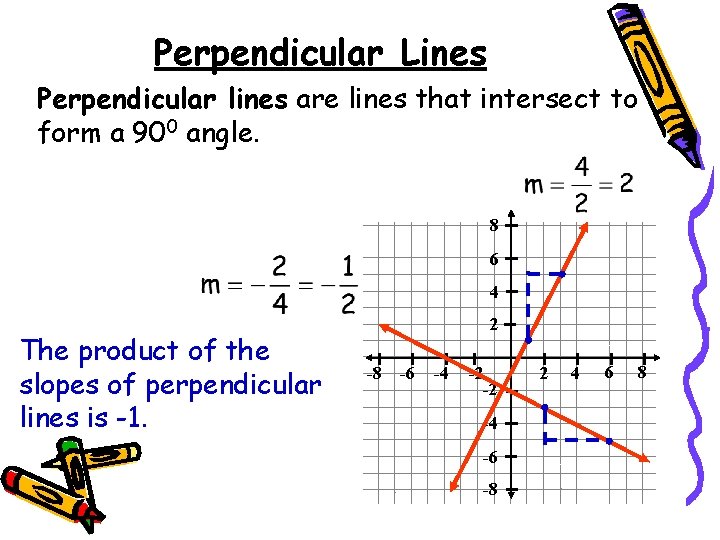
Perpendicular Lines Perpendicular lines are lines that intersect to form a 900 angle. 8 6 4 The product of the slopes of perpendicular lines is -1. 2 -8 -6 -4 -2 -2 -4 -6 -8 2 4 6 8

Example 1 Determine whether these lines are perpendicular. and y = -3 x - 2 m = -3 Since the product of the slopes is -1, the lines are perpendicular.

Example 2 Determine whether these lines are perpendicular. y = 5 x + 7 m=5 and y = -5 x - 2 m = -5 5 x (-5) = -25 Since the product of the slopes is not -1, the lines are not perpendicular.

Practice Determine whether these lines are perpendicular. 1) 2 y – x = 2 and y = -2 x + 4 1. no 2) 4 y = 3 x + 12 and -3 x + 4 y – 2 = 0 2. no

Example 3 Write an equation for the line containing (-3, -5) and perpendicular to the line y = 2 x + 1. First, we need the slope of the line y = 2 x + 1. m=2 Second, we need to find out the slope of the line that is perpendicular to y = 2 x + 1. Lastly, we use the slope formula to find our equation. y = mx + b y = 2 x + b − 5 = 2(− 3) +b − 5 = − 6 +b b=1 y = 2 x + 1

Practice Write an equation for the line containing the given point and perpendicular to the given line. 1) (0, 0); y = 2 x + 4 y = −½x 2) (-1, -3); x + 2 y = 8 Y = − 2 x +1

Homework p. 144, 1 -9, 15 -17