2 26 Addition rule union and intersections Topic

2. 26 Addition rule- union and intersections

Topic: Addition Rule- union, intersection EQ: How can we find the probability of events? 1. A cylinder has a radius of 3 and a height of 20. If you put three 3 inch radius tennis balls inside this cylinder, how much empty space is there? 2. Janae has a mold to make her own custom crayons in the shape pictured to the left. Janae can buy blocks of wax that are cubes with sides of length 5 cm. How many crayons can Janae make?

Warm Up Continued 3. A sculptor wants to remove stone from a cylindrical block 3 feet high and turn it into a cone. The diameter of the base of the cone and cylinder is 2 feet. How much stone must the sculptor remove? 4.

Warm Up #1 �A cylinder has a radius of 3 and a height of 20. If you put three 3 inch radius tennis balls inside this cylinder, how much empty space is there? Cylinder Sphere Calculations

Warm Up Answers #2 �Janae has a mold to make her own custom crayons in the shape pictured to the left. Janae can buy blocks of wax that are cubes with sides of length 5 cm. How many crayons can Janae make? Janae can make 5 candles

Warm Up #3 Answers �A sculptor wants to remove stone from a cylindrical block 3 feet high and turn it into a cone. The diameter of the base of the cone and cylinder is 2 feet. How much stone must the sculptor remove?

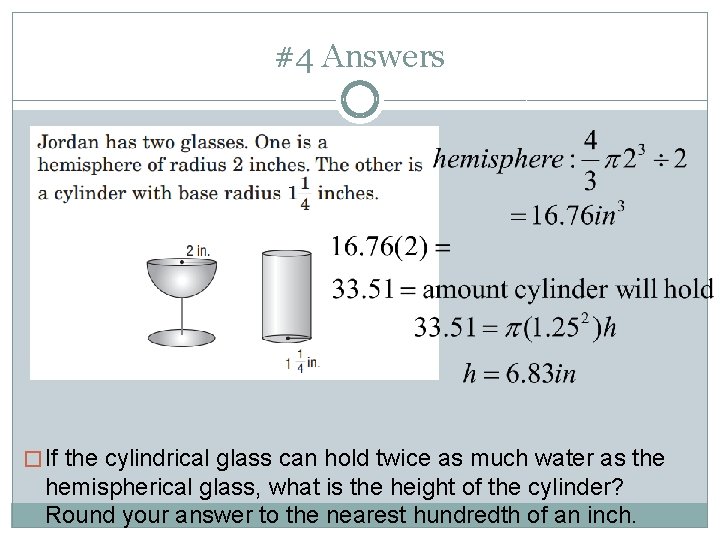
#4 Answers � If the cylindrical glass can hold twice as much water as the hemispherical glass, what is the height of the cylinder? Round your answer to the nearest hundredth of an inch.

EQ: How can we find the probability of events? �SWBAT solve probability problems involving the general addition rule, union, and intersection �S-CP-1 ; 3. 3. a. i �S-CP-7 ; �Given 2 MC and 2 CR problems, students will solve probability problems involving additional rule, union and intersection with 75% accuracy of higher.

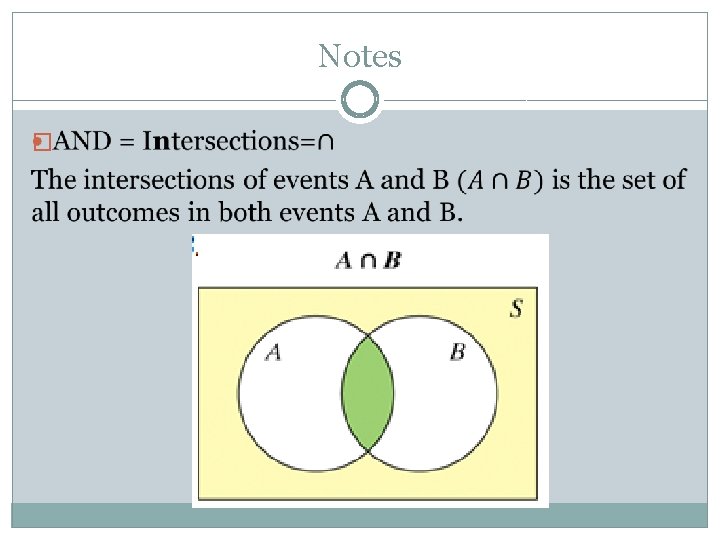
Notes �

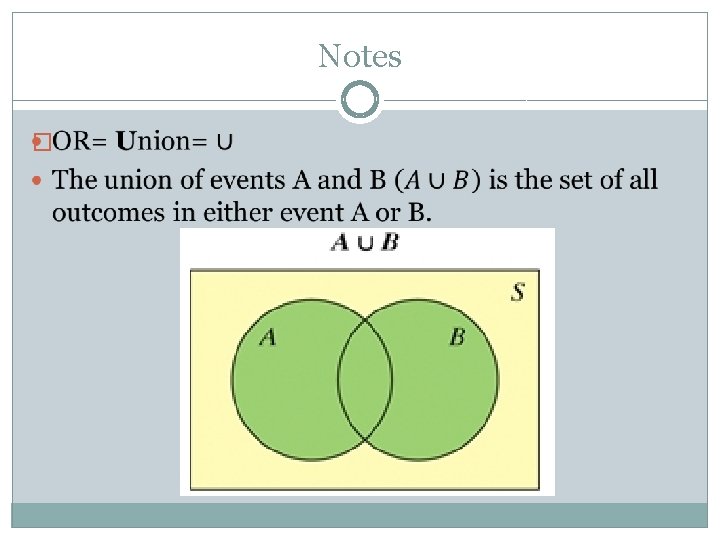
Notes �

Addition Rule for Probability (part 1) �

Example #1 �

Whiteboards: Independent �

Whiteboards: Independent �

Addition Rule Part 2 �

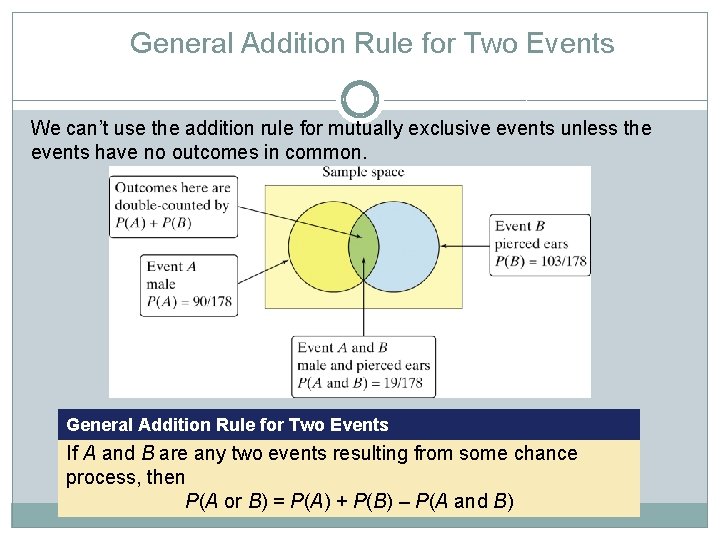
General Addition Rule for Two Events We can’t use the addition rule for mutually exclusive events unless the events have no outcomes in common. General Addition Rule for Two Events If A and B are any two events resulting from some chance process, then P(A or B) = P(A) + P(B) – P(A and B)

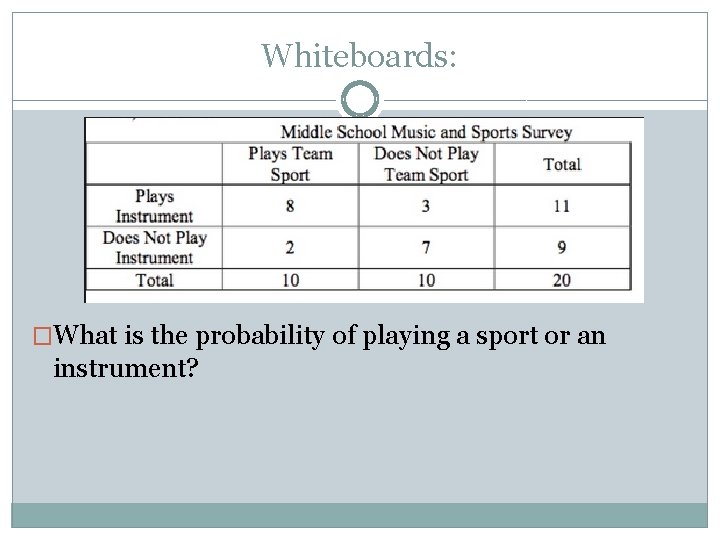
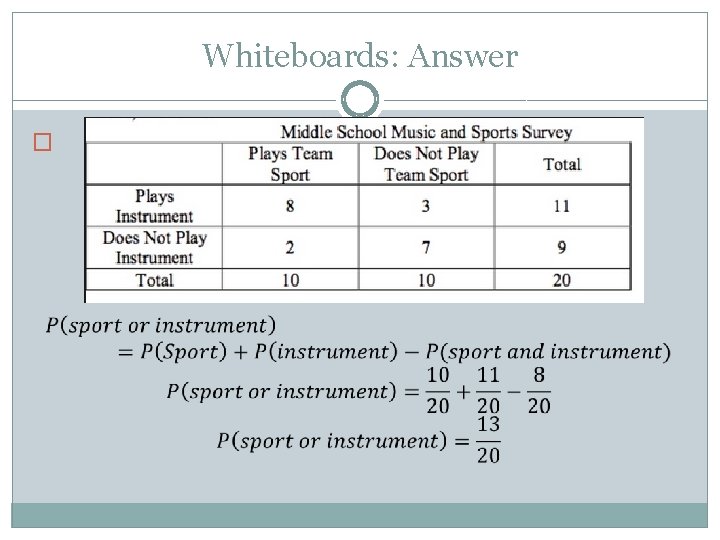
Whiteboards: �What is the probability of playing a sport or an instrument?

Whiteboards: Answer �

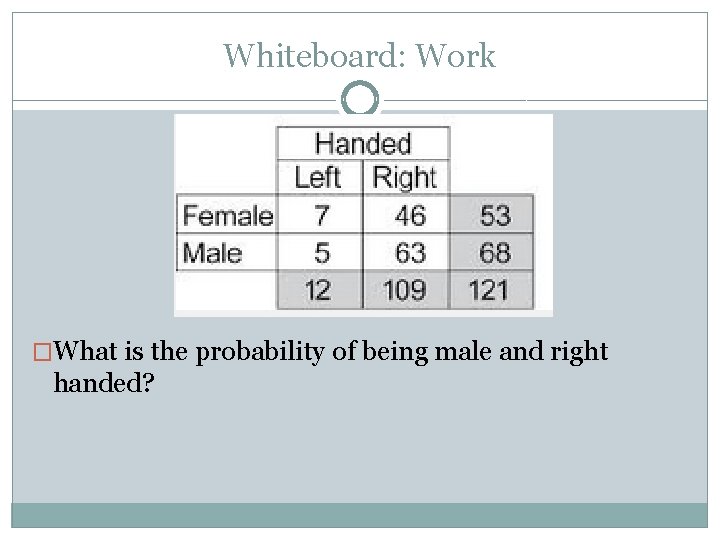
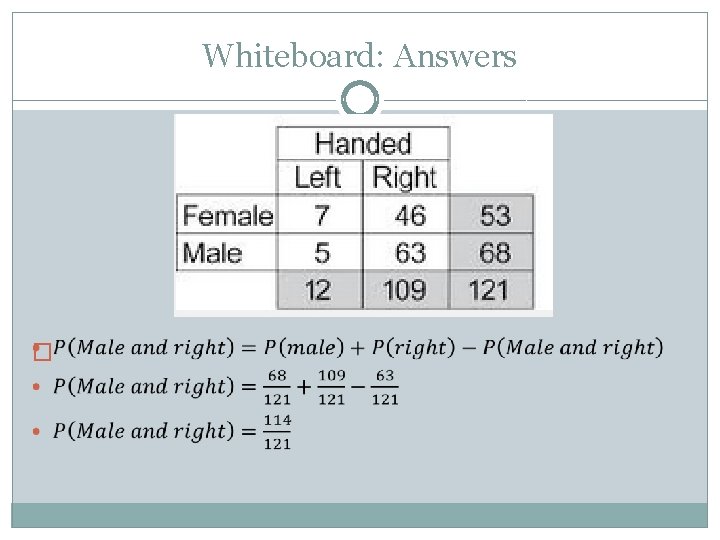
Whiteboard: Work �What is the probability of being male and right handed?

Whiteboard: Answers �

Whiteboard: Independent Work Find the probability for female or being right handed.

Whiteboard: Answers �

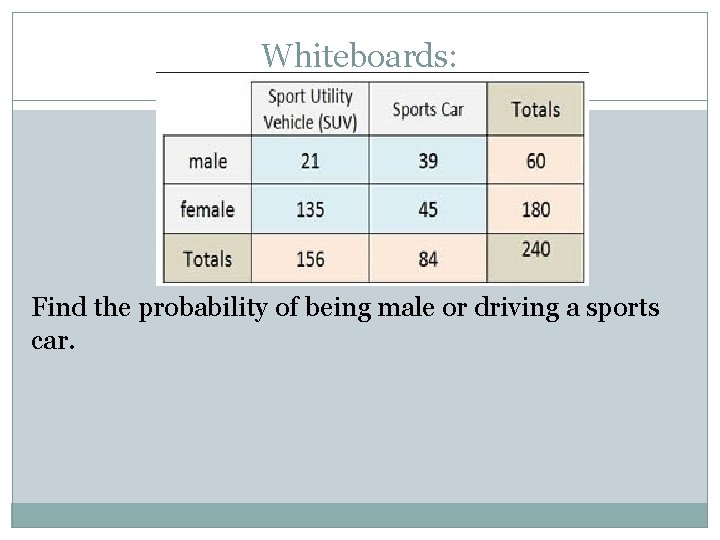
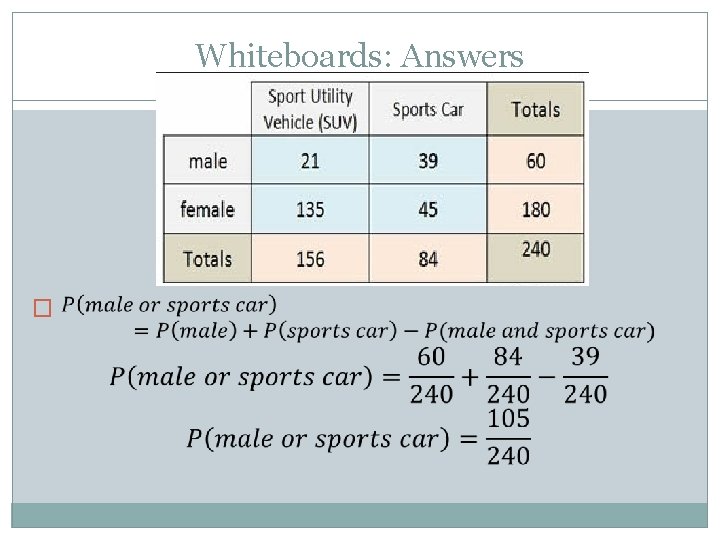
Whiteboards: Find the probability of being male or driving a sports car.

Whiteboards: Answers �

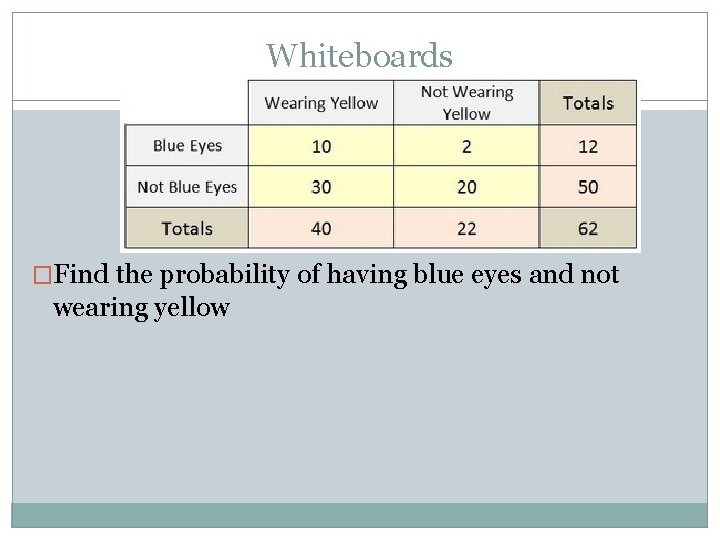
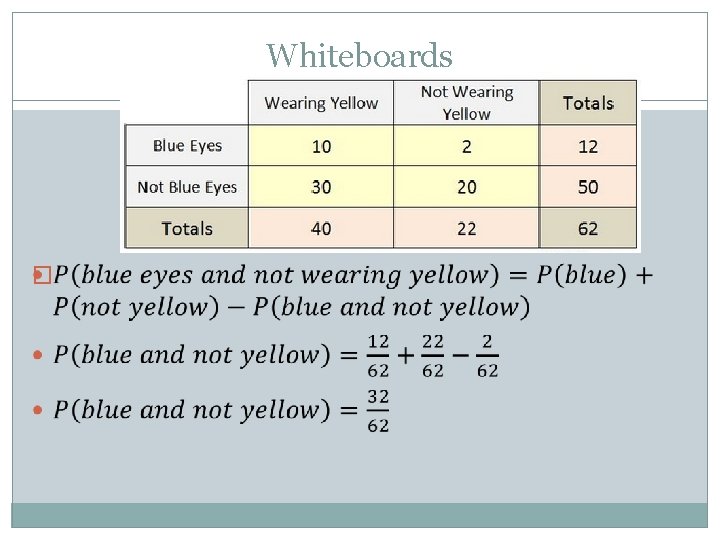
Whiteboards �Find the probability of having blue eyes and not wearing yellow

Whiteboards �

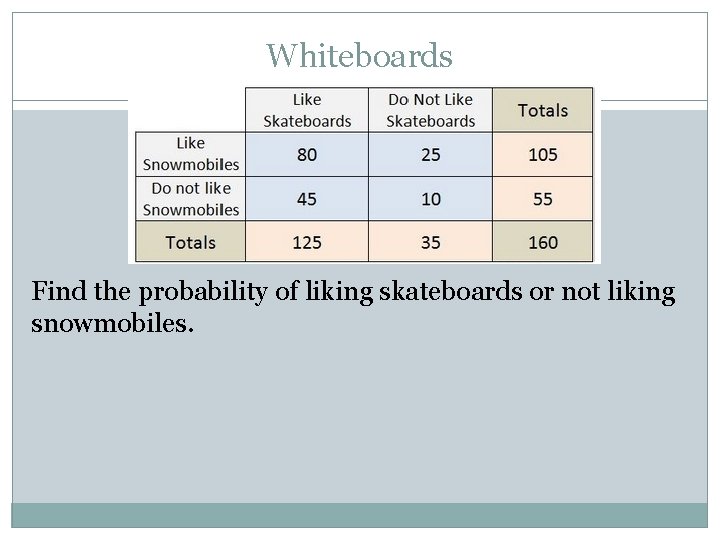
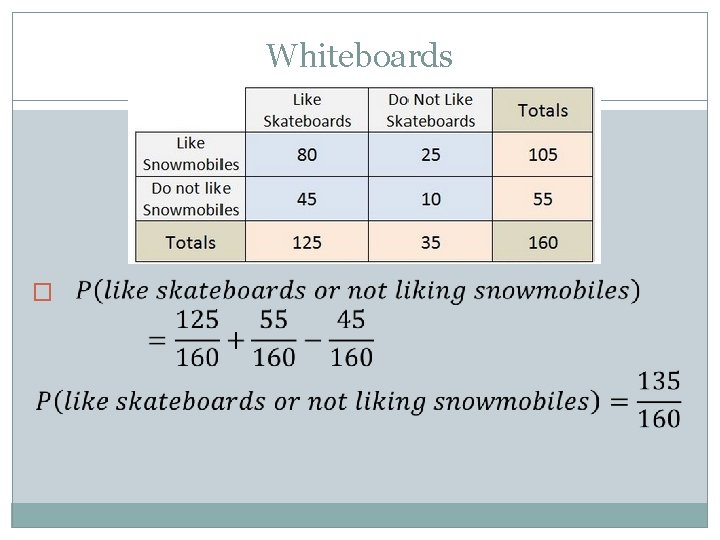
Whiteboards Find the probability of liking skateboards or not liking snowmobiles.

Whiteboards �

Example #2 �

Whiteboards- Independent �

Whiteboards- Independent �

Summary �

Practice Problem #1 �

Work �

Practice Problem #2 �In a pet store, there are 6 puppies, 9 kittens, 4 gerbils and 7 parakeets. If a pet is chosen at random, what is the probability of choosing a puppy or a parakeet?

Answers to #2 �

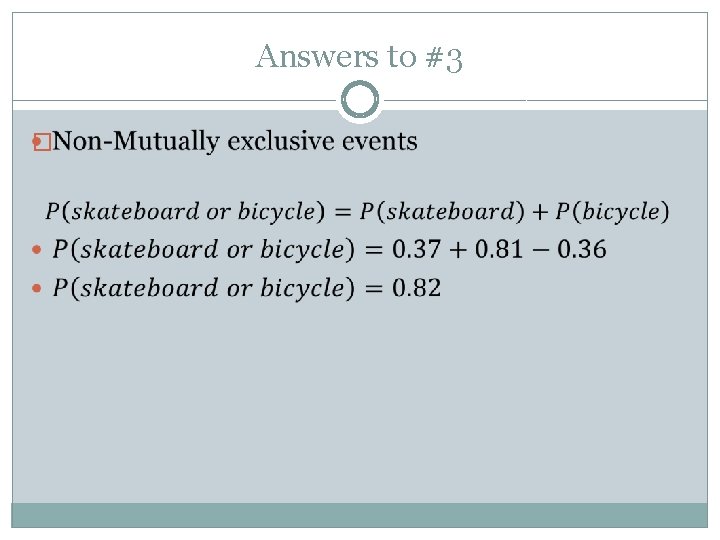
Practice Problem #3 �The probability of a Colorado teenager owning a skateboard is 0. 37, of owning a bicycle is 0. 81, and of owning both is 0. 36. If a Colorado teenager is chosen at random, what is the probability that the teenager owns a skateboard or a bicycle?

Answers to #3 �

Practice Problem #4 �A number from 1 to 10 is chosen at random. What is the probability of choosing a 5 or an even number?

Answers Practice Problem #4 �

Practice Problem #5 �A single 6 -sided die is rolled. What is the probability of rolling a number greater than 3 or an even number?

Answers Practice Problem #5 �

Practice Problem #6 �In a group of 101 students, 30 are freshman and 41 are sophomores. Find the probability that a student picked from this group at random is either a freshman or a sophomore.

Answers Practice Problem #6 �

Practice Problem #7 In a group of 101 students 40 are juniors, 50 are female, and 22 are female juniors. Find the probability that a student picked from this group at random is either junior or female.

Answers Practice Problem #7 �

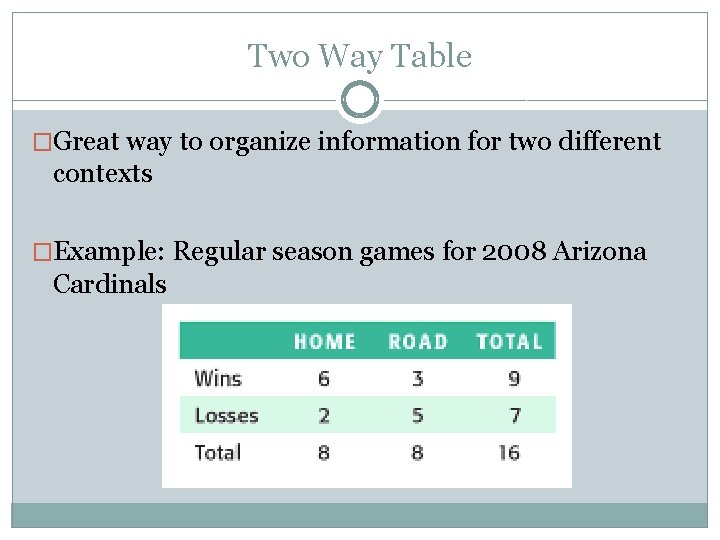
Two Way Table �Great way to organize information for two different contexts �Example: Regular season games for 2008 Arizona Cardinals

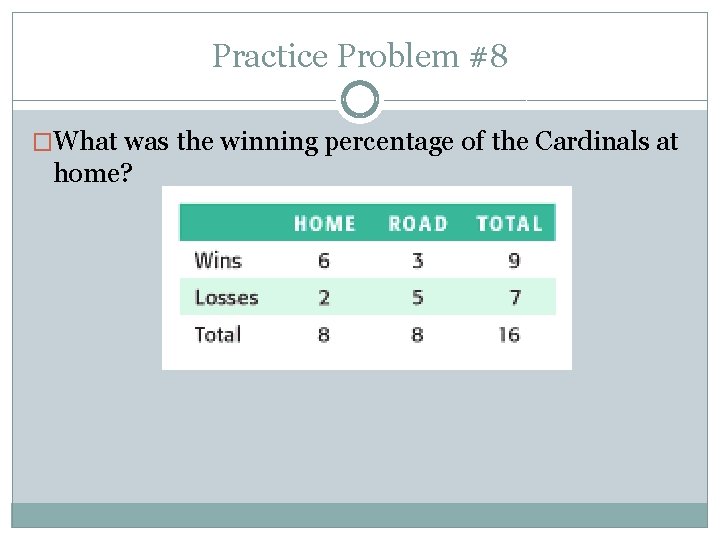
Practice Problem #8 �What was the winning percentage of the Cardinals at home?

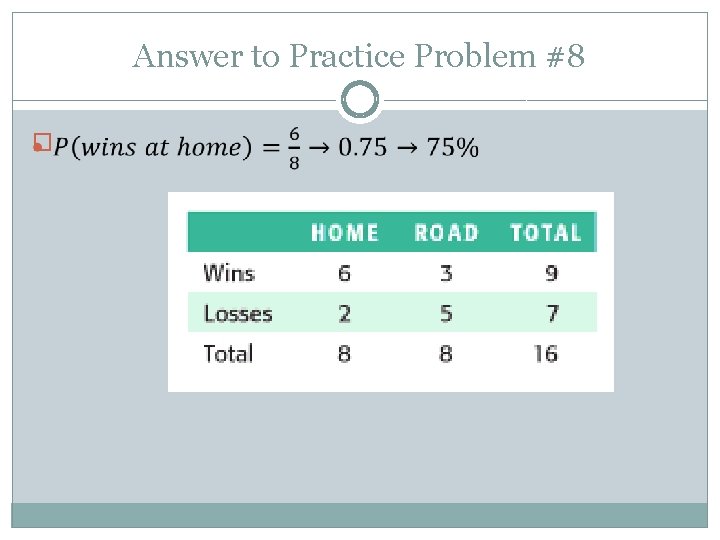
Answer to Practice Problem #8 �

Practice Problem #9 �Probability of total wins �Probability of losses on the road �Probability of total losses

Answers Practice Problem #9 �

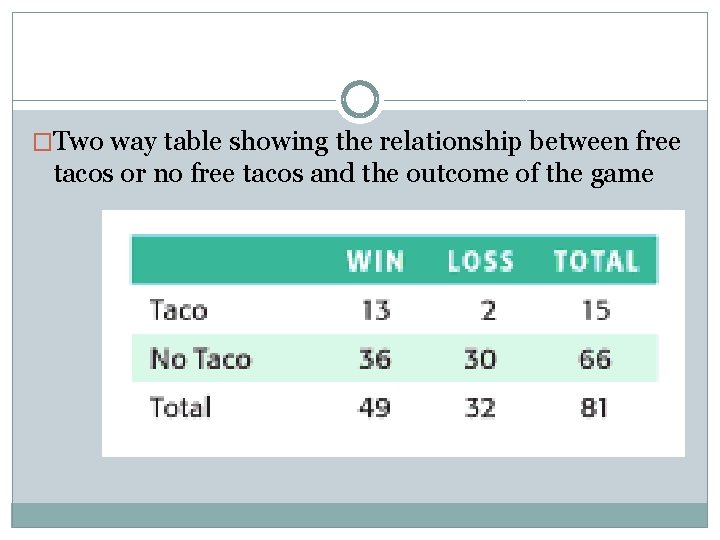
�Two way table showing the relationship between free tacos or no free tacos and the outcome of the game

Find the probability of a free taco and a win

Find the probability of a free taco and a win �

WORKSHEET

Worksheet Answers #1 �

Worksheet Answers #2 �

DOL #1 and #2 1. What is the probability of wins on the road? In a group of 365 students 120 are seniors, 80 are female, and 22 are female seniors. Find the probability that a student picked from this group at random is either senior or female.

DOL #3 and #4 3. In a pet store, there are 12 puppies, 5 kittens, 6 snakes, and 10 rabbits. Find the probability of selecting a rabbit or snake. 4. A spinner has 4 equal sectors colored yellow, blue, green, and red. What is the probability of landing on red or blue after spinning this spinner?

DOL #1 and #2 ANSWERS � �

DOL #3 and #4 - Answers � �