2 2 The Revised Simplex Method The simplex

§ 2. 2 The Revised Simplex Method The simplex method for LP : G. B. Dantzig 1951 Key idea: Phase 1: find a bfs of Note that an LP may not have a solution Example min s. t. 2008/3/4 Shi-Chung Chang, NTUEE, GIIE, GICE 1

Phase 2 Allow one of the zero components of the bfs to become positive and force one of the original positive components to become zero. => How to pick “entering” and “leaving” component Cost Traditional form of the simplex method: Tableau => read by yourself Here we consider matrix form for conciseness of presentation and later developments. 2008/3/4 Shi-Chung Chang, NTUEE, GIIE, GICE 2

SLP: s. t. Assume P(A)=m. Partition A=[B: D] B: m linearly indep. columns of A (Assume the first m cols. ) (SLP) subject to 2008/3/4 (3. 1) Shi-Chung Chang, NTUEE, GIIE, GICE 3

If When and a basic solution from (3. 1) (note that may not ≥ 0 ) (3. 2) Substituting(3. 2) into the cost function (3. 3) Define (3. 4) as the relative cost vector => To minimize Z, we need only adjust Q: How? 2008/3/4 Shi-Chung Chang, NTUEE, GIIE, GICE 4

Example subject to + + =2 =5 =6 In matrix form. 2008/3/4 Shi-Chung Chang, NTUEE, GIIE, GICE 5

2008/3/4 Shi-Chung Chang, NTUEE, GIIE, GICE 6

Define the vector of simplex multipliers Compute in two steps: Assume that If If is non degenerate is optimal and increasing 2008/3/4 it does not pay to increase then the cost Z can possible be decreased by Shi-Chung Chang, NTUEE, GIIE, GICE 7

Q: (1) any limitations on increasing ? (2) If there are more than one component of r < 0 => which should we change to increase? Simplex method chooses one entering variable, Normally one with the most negative Q: which component should leave? the first one to reach 0 => 2008/3/4 satisfied again. Shi-Chung Chang, NTUEE, GIIE, GICE 8

If we consider bringing into the basis, i. e. , as the entering variable => => 2008/3/4 Shi-Chung Chang, NTUEE, GIIE, GICE 9

Mathematically, let => be the new value vector of => The ith component of is zero when i. e. when 2008/3/4 Shi-Chung Chang, NTUEE, GIIE, GICE 10

To maintain feasibility, the smallest of these ratios for i where >0 determines how large can be. Say, it happens at l th components of Þ The new bfs has and leaves the basis while R earranging 2008/3/4 enters , w e can get Shi-Chung Chang, NTUEE, GIIE, GICE 11

Revised Simplex Algorithm( one iteration) Step 1: Giving is the basis B such that Step 2: Solve to get Step 3 : Calculate If r ≥ 0 => optimal solution achieved, STOP Find K = arg Step 4 : Solve Step 5 : Find for y If , => unbounded solution, STOP Step 6 : Update the basic solution Step 7 : Update the basis Return to step 2 2008/3/4 Shi-Chung Chang, NTUEE, GIIE, GICE 12

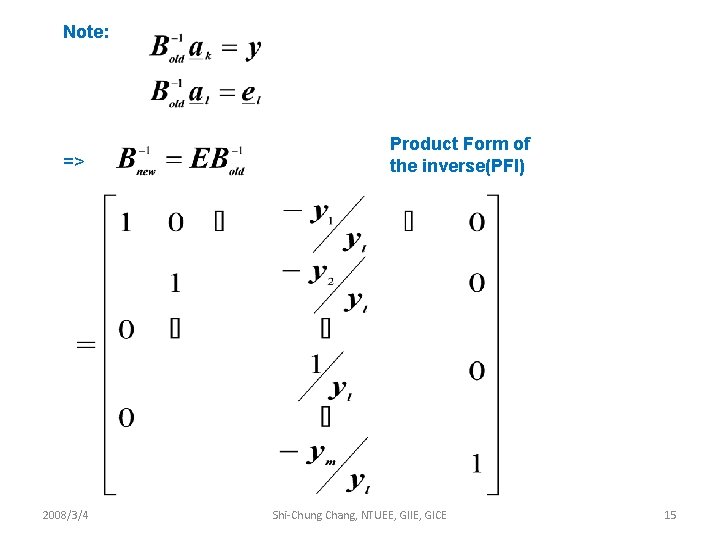
How to Update Basis Note that in the simplex algorithm we need to solve (step 2) (step 4) Where B’s differ by only one column between any two subsequent iterations. => How to calculate B’s efficiently? 2008/3/4 Shi-Chung Chang, NTUEE, GIIE, GICE 13

Recall (rank one update) 2008/3/4 Shi-Chung Chang, NTUEE, GIIE, GICE 14

Note: => 2008/3/4 Product Form of the inverse(PFI) Shi-Chung Chang, NTUEE, GIIE, GICE 15

Some Computational Aspects Let be the elementary matrices after K pivot iterations. => • For large-scale problems, store followers: 2008/3/4 ‘s as vector and update Shi-Chung Chang, NTUEE, GIIE, GICE and y as 16

• What if is small in pivoting? Þ Use LU or QR decompositions in computing If B is the current basis Note that => upper Hessenberg 2008/3/4 Shi-Chung Chang, NTUEE, GIIE, GICE 17

Using a sequence of elimination steps on H: • • Store QR-decomposition Do givens transformation on H • The simplex method is theoretically an exponential algorithm In practice, 2(n + m) iterations, i. e. , a linear function of (n + m) 2008/3/4 Shi-Chung Chang, NTUEE, GIIE, GICE 18

Convergence and Degeneracy Convergence: If the objective function value strictly decreases after every iteration, the simplex algorithm never repeats a basis and it converges in a finite number of iterations. why? Degeneracy: If for a such that => x is a degenerate 2008/3/4 Shi-Chung Chang, NTUEE, GIIE, GICE 19

Property: in the pivoting step, => i. e. no change in cost. => Problem: cycling among degenerate => no guarantee of convergence => need an anti-cycling algorithm 2008/3/4 Shi-Chung Chang, NTUEE, GIIE, GICE 20

How to get an initial feasible solution? (p) Þ (PH 1) subject to 2008/3/4 Shi-Chung Chang, NTUEE, GIIE, GICE 21

• (P) has a feasible solution in (PH 1) Q: • can solve (PH 1) using revised simplex with as the initial feasible solution 2008/3/4 Shi-Chung Chang, NTUEE, GIIE, GICE 22

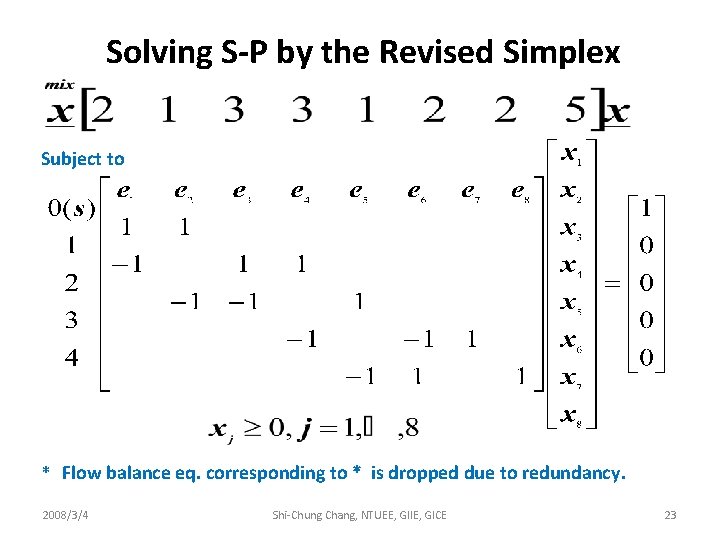
Solving S-P by the Revised Simplex Subject to * Flow balance eq. corresponding to * is dropped due to redundancy. 2008/3/4 Shi-Chung Chang, NTUEE, GIIE, GICE 23

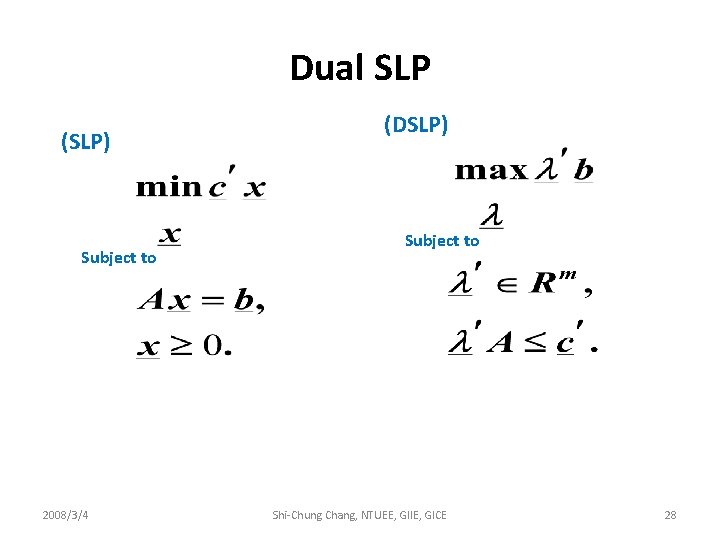
Chapter 3 Duality § 3. 1 Dual LP Consider (SLP) Subject to 2008/3/4 Shi-Chung Chang, NTUEE, GIIE, GICE 24

Dual Viewpoint • From the optimality condition, if optimal solution to SLP => corresponding partition of A matrix such that Note that in Simplex Method, we have

Dual Viewpoint (Cont. ) Note that The l’ we are looking for must satisfy (3. 5) for any The root of (3. 5) comes from So, Note that l*’ in (3. 5) and (3. 6) satisfies (3. 7) and (3. 8).

Dual Objective Function Now consider the objective function From inequality (3. 8) that then for any bfs we have and from (3. 9) l*’ is the one that leads to the maximum while satisfying (3. 7) and (3. 8) value

Dual SLP (SLP) Subject to 2008/3/4 (DSLP) Subject to Shi-Chung Chang, NTUEE, GIIE, GICE 28