2 2 Linear Transformations in Geometry For an

2. 2 Linear Transformations in Geometry For an animation of this topic visit http: //www. ies. co. jp/math/java/misc/don_trans. html

Library of basic matrices What matrices do we have in our library of basic matrices?

Library of basic matrices What matrices do we have in our library of basic matrices? We should have these basic matrices in our library Identity Matrix Rotations Scaling

Problem 32

Problem 32 Answer: 3 I

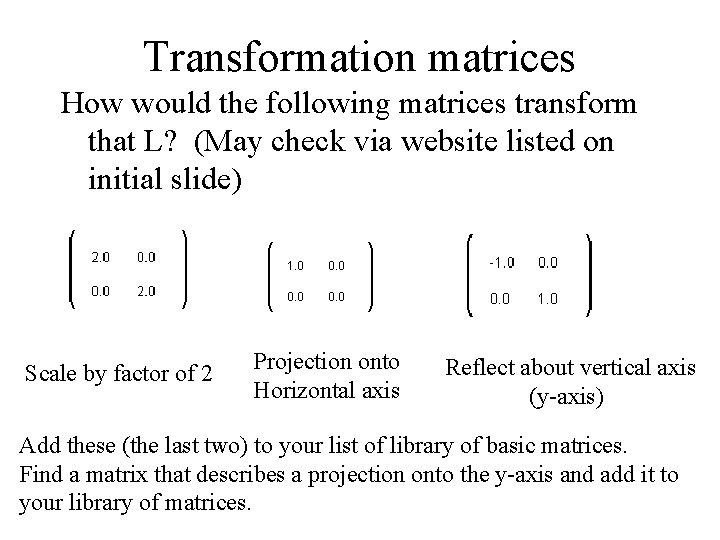
Transformation matrices Use your knowledge of matrix multiplication (and your library of matrices) to predict what affect these matrices would have on our dog. How would the following matrices transform that L? (May check via website listed on initial slide)

Transformation matrices How would the following matrices transform that L? (May check via website listed on initial slide) Scale by factor of 2 Projection onto Horizontal axis Reflect about vertical axis (y-axis) Add these (the last two) to your list of library of basic matrices. Find a matrix that describes a projection onto the y-axis and add it to your library of matrices.

What type of Linear Transformation results from these matrices (Answer on next slide)

What type of Linear Transformation results from these matrices Reflect about Horizontal axis Horizontal Shear rotated 45 degrees and scaled by root 2 Add the first one to your library of basic matrices. We will generalize the last two before adding them.

What do you think that these matrices would do to our dog?

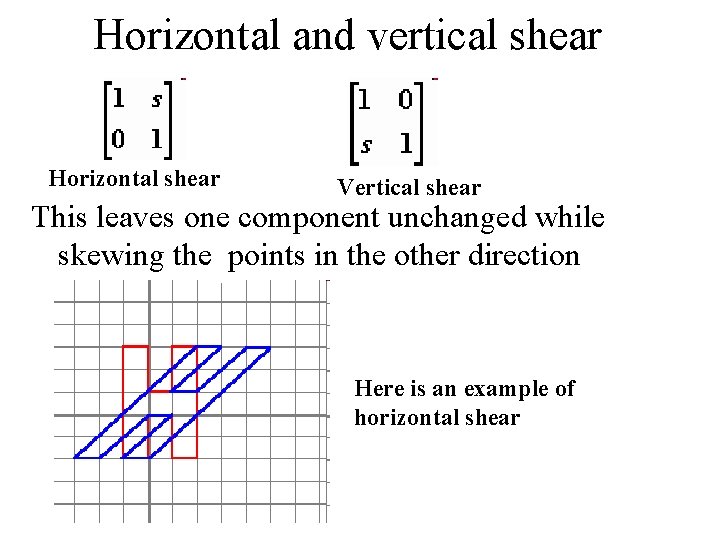
Horizontal and vertical shear Horizontal shear Vertical shear This leaves one component unchanged while skewing the points in the other direction Here is an example of horizontal shear

Recall: Scaling For any positive constant k, the matrix Defines a scaling by k times. If k is between 0 and 1 then the scaling is a contraction. If k >1 then the scaling is a dilation (enlargement)

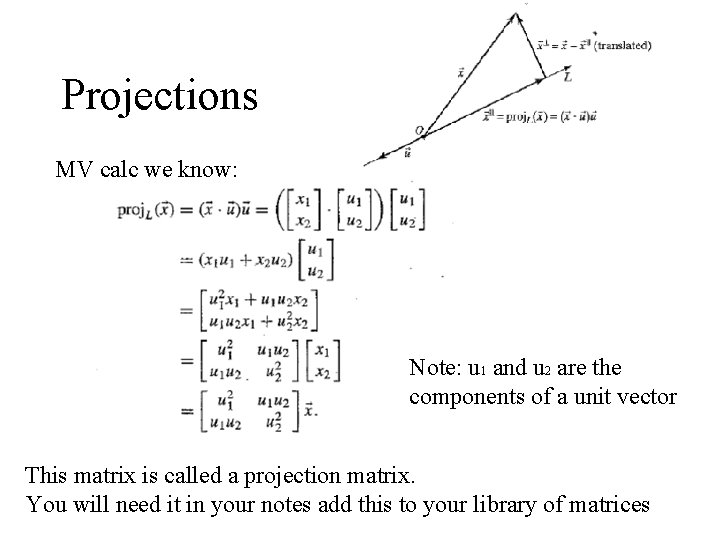
Projections Consider a line L in the coordinate plane, running through the origin. Any vector in _ can be written as + = The transformation T(x) = projection onto x is called the

Projections MV calc we know: Note: u 1 and u 2 are the components of a unit vector This matrix is called a projection matrix. You will need it in your notes add this to your library of matrices

Example 2 Find the matrix A of the projection onto the Line spanned by

Example 2 Solution

From your knowledge of matrix multiplication what would these matrices do to our dog?

One directional scaling (Note this is not in our text book) These matrices multiply one component of b while leaving the other unchanged. For example Notice that the x components are halved while the y is unchanged

Combined scaling This will multiply the x component by r and the y component by s Horizontal scaling Vertical scaling Combined scaling Add these to our library of basic matrices What would a single component scaling or combined scaling matrix look like in Rn?

What matrices should we have in our library of basic matrices?

What matrices should we have in our library of basic matrices? Identity Matrix Projection Matrices Projection onto x-axis Projection onto y-axis Rotation Matrix One directional Scaling Mixed Scaling Horizontal Shear Vertical Shear Scaling

Homework: p. 65 1 -6, 8 -10, 26 a-c only, 30, 31

Rotations