2 2 Linear Models Correlation Linear functions Y





















- Slides: 29

2. 2 Linear Models & Correlation

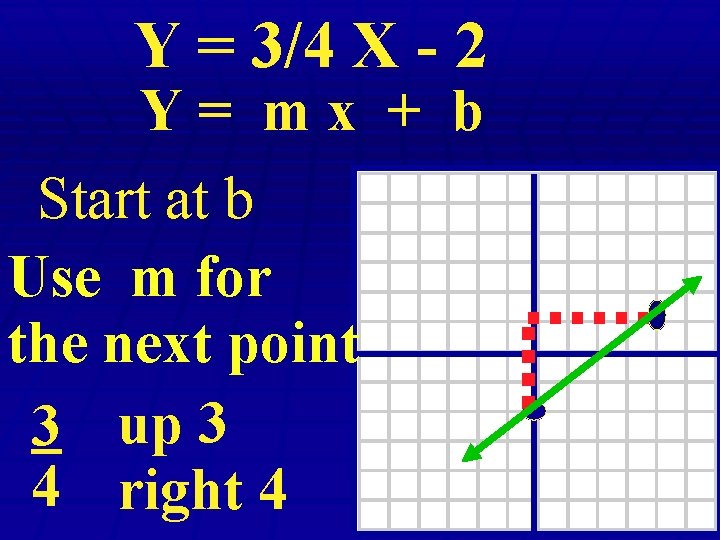
Linear functions Y = am x + b slope m = y 2 y 1 On the calculator a=m y intercept

Y = 3/4 X - 2 Y= mx + b Start at b Use m for the next point 3 up 3 4 right 4

Find an equation through (1, 5) and (-2, -1). Need m and b m = y 2 - y 1 m = -1 - 5 m = -6 -2 - 1 -3 x 2 - x 1 m =2

Find an equation through (1, 5) and (-2, -1). Need m and b y= mx + b y = 2 x +3 5 = 2(1) + b 5=2+b 3=b

Find an equation through (1, 5) and (-2, -1). Need m and b Shortcut : Use Calculator.

Find an equation through (1, 5) and (-2, -1). Put the ordered pairs into 2 Stat 1 2 -2 Edit 5 -1

Find an equation through (1, 5) and (-2, -1). Stat Calc 4: Lin Reg (ax + b) y = ax + b a=2 b=3

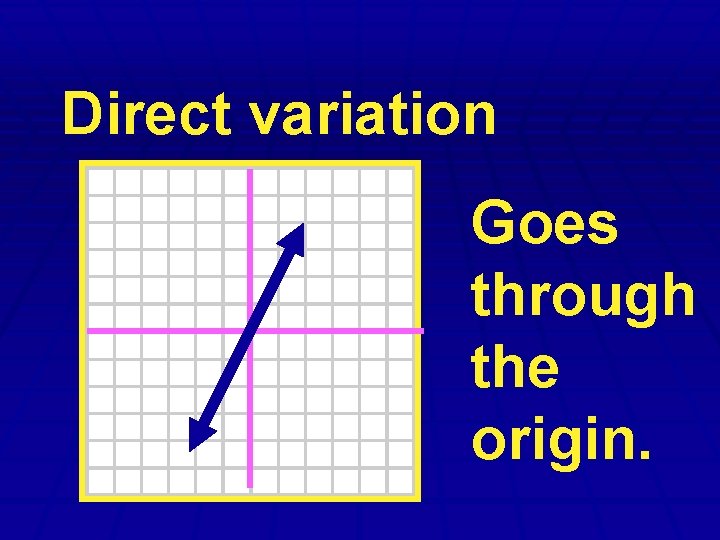
Direct Variation y=kx Y varies directly. k is the constant of variation.

Y=kx same as y = k x

How to find k y x y = k x 2 8 8 3 12 =4 2 4 16 5 20 12 = 4 3

Direct variation Goes through the origin.

Not direct

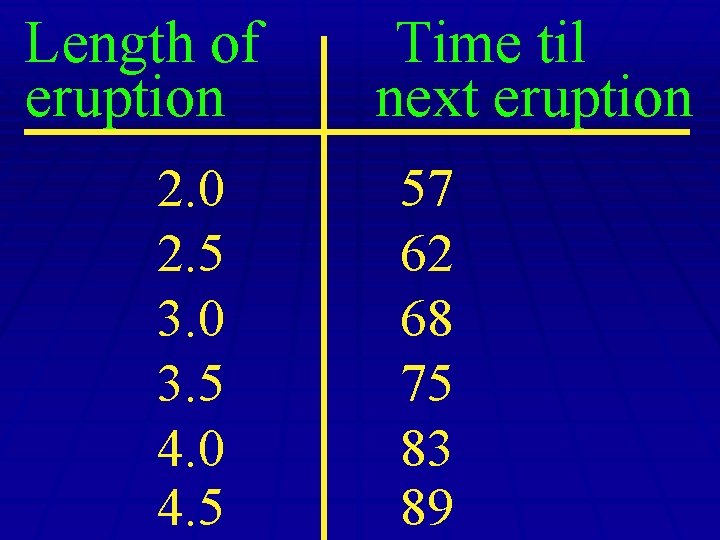
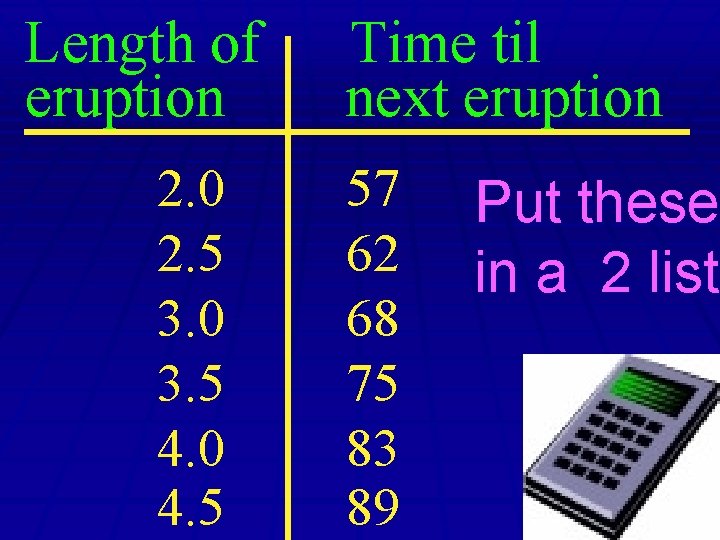
Old Faithful Problem

Length of eruption 2. 0 2. 5 3. 0 3. 5 4. 0 4. 5 Time til next eruption 57 62 68 75 83 89

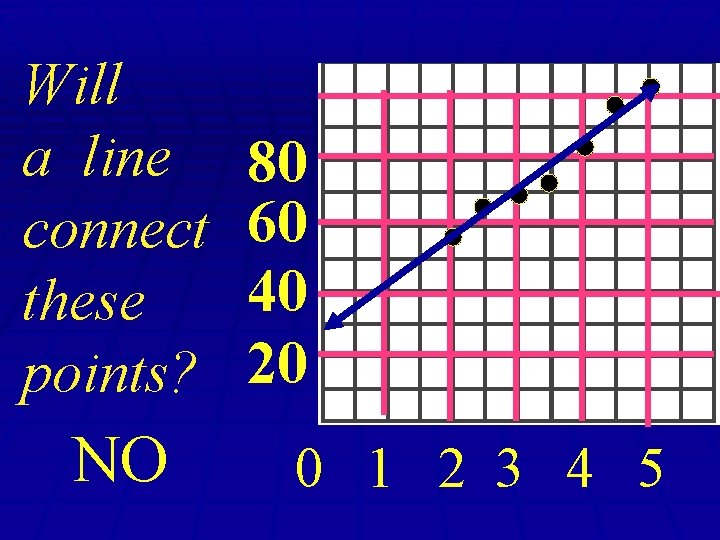
2. 0 2. 5 3. 0 3. 5 4. 0 4. 5 57 62 68 75 83 89 80 60 40 20 0 1 2 3 4 5

Will a line connect these points? NO 80 60 40 20 0 1 2 3 4 5

This scatter plot has numbers close to the line. You can write an equation to make a prediction.

Try to fit the line through the middle of the points. Choose two points on the line. ( , ) Find m. Find b.

Length of eruption 2. 0 2. 5 3. 0 3. 5 4. 0 4. 5 Time til next eruption 57 62 68 75 83 89 Put these in a 2 lists list

Stat Calc 4: Lin Reg (ax + b) y = ax + b y = 13. 1 X + 29. 6 a = 13. 1 correlation coefficient b = 29. 6 2 r =. 995 r =. 9976

Stat Calc 4: Lin Reg (ax + b) y = ax + b To turn r on, go a = 13. 1 Catalogue b = 29. 6 Diagnostic On 2 r =. 995 r =. 9976

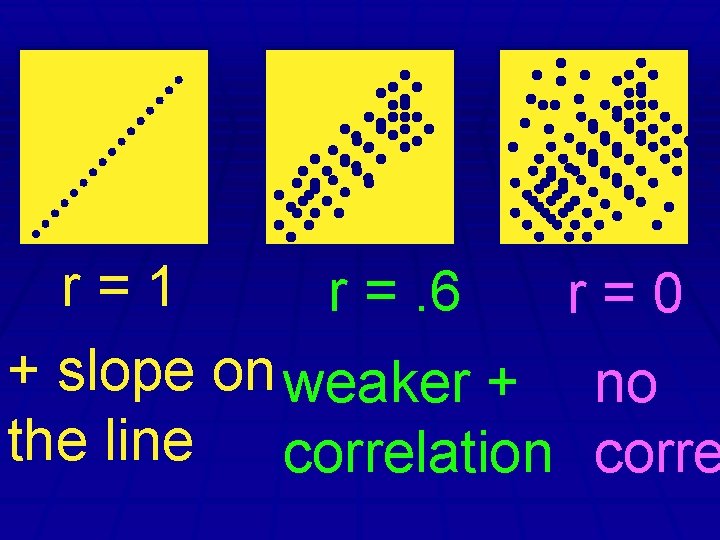
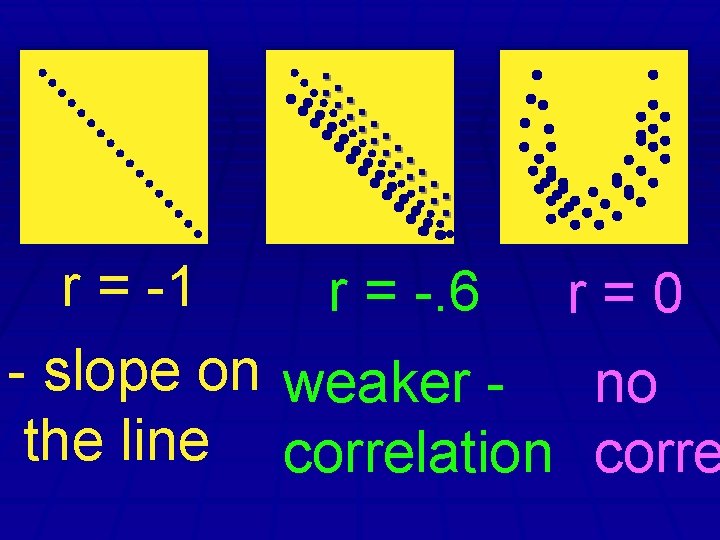
The correlation coefficient tells you how strong the line relation is. Are the dots in the scatter close to the line, or far awa

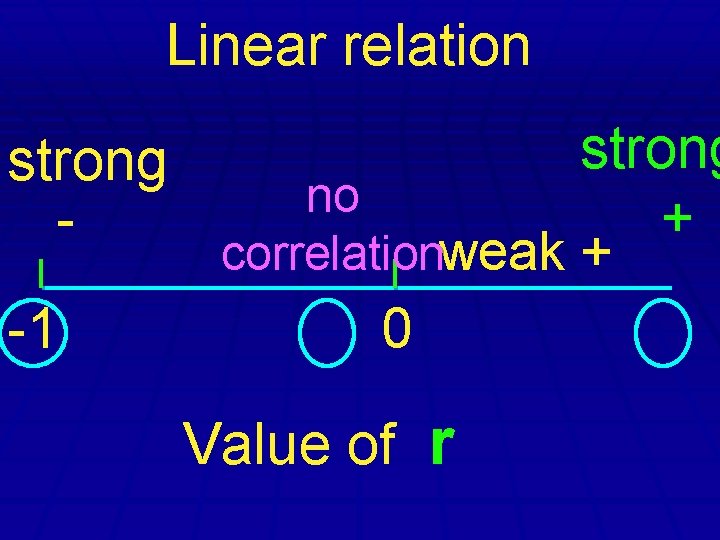
The correlation coefficient between -1 and +1. -1 < r < 1

r=1 r =. 6 r=0 + slope on weaker + no the line correlation corre

: : : r = -1 - slope on the line r = -. 6 r=0 weaker no correlation corre

Linear relation strong l -1 strong + no correlation weak + l 0 Value of r

In our Old Faithful problem y = ax + b a = 13. 1 b = 29. 6 2 r =. 995 r =. 9976 What does tha tell you?

Aspire to climb as high as you can dream.