2 2 Graphing quadratic functions 1 Standard Form

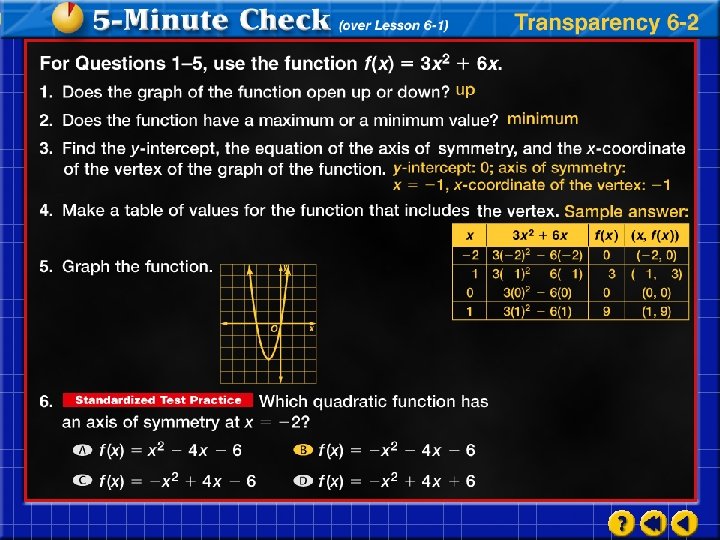
2. 2 Graphing quadratic functions 1. Standard Form – f(x)=ax 2 + bx + c. 3. y–intercept is c 4. Axis of symmetry and x-coordinate of the vertices – 5. The y-coordinate of the vertex is the maximum or minimum value.

2. 2 continued o If a > 0 then the parabola opens up and has a minimum value. o If a < 0 then it opens down and has a maximum value. o Minimum/Maximum point and min/max value are not the same. Min/Max value is the y-coordinate of the vertex. Min/Max point is the ordered pair (x, y) of the vertex.

1) f(x) = x 2 + 8 x + 9 o o Find the y-intercept 9 Find the axis of symmetry -8/2 = -4; x=4 (-4, -7) Find the vertex Find the maximum or minimum value -7, min. o Does the graph open up or down? Opens up

Find the vertex, a. o. s, y-intercept, direction and width of the parabola, table of points and graph. Find the maximum or minimum value. 2) y = 2 x 2 – 8 x + 6

3. f(x) = x 2 + 3 x – 1 A) B) C) D) V (-1. 5, -. 3. 25) a. o. s x=-1. 5 Y-int = -1 a=1, Opens up Standard width Minimum = -3. 25 x -3 -2 -3/2 (-1. 5) -1 0 f(x) -1 -3 -13/4 -3 -1 (-3. 25)

2. 2 examples 4. f(x) = 2 – 4 x + x 2 a. Find the y-intercept, the equation of the axis of symmetry, the vertex. b. Make a table of values that includes the vertex. c. Graph the function a. 2, x = 2, (2, -2) b. (0, 2), (1, -1), (2, -2), (3, -1), (4, 2)

2. 2 Classwork 5. f(x) = -x 2 + 2 x + 3 a. Determine whether the function has a maximum and minimum value. b. State the maximum and minimum value of the function. a. Maximum value b. 4

2. 2 Application 1. A souvenir shop sells about 200 coffee mugs each month for $6 each. The shop owner estimates that for each $. 50 increase in the price, he will sell about 10 fewer coffee mugs per month. a. How much should the owner charge for each mug in order to maximize the $8 monthly income from their sales? b. What is the maximum monthly income the owner can expect to make from these items? $1280