2 2 CONDITIONAL STATEMENTS Chapter 2 OBJECTIVES Identify

2 -2 CONDITIONAL STATEMENTS Chapter 2

OBJECTIVES Identify, write, and analyze the truth value of conditional statements. Write the inverse, converse, and contrapositive of a conditional statement.

2. 2 CONDITIONAL STATEMENTS You can describe some mathematical relationships using a variety of if-then statements. A conditional statement _______________ - Let p be the ________ - q be the___________ Hypothesis – the ____part of the statement. Conclusion – the _______ part of the statement. _________– show the set of things that satisfy the hypothesis lies inside the set of things that satisfy the conclusion.

IDENTIFYING THE HYPOTHESIS AND THE CONCLUSION What are the hypothesis and the conclusion of the conditional? If an animal is a robin, then the animal is a bird. Hypothesis (p): Conclusion (q): If an angle measures 130 degrees, then the angle is obtuse. Hypothesis (p): Conclusion (q):

WRITING A CONDITIONAL How can you write the following statement as a conditional? Vertical angles share a vertex. Step 1 – identify the hypothesis and the conclusion. Step 2 – write the conditional.

GUIDED PRACTICE Write a conditional statement from the sentence: “Dolphins are mammals”. Write a conditional statement from the sentence “Two angles that are complementary are acute. ”

TRUTH VALUE A conditional statement has a _____of either true (T) or false (F). It is false only when the hypothesis is true and the conclusion is false. To show a conditional is false, find only ____ counterexample for which the hypothesis is true and the conclusion is false.

FINDING THE TRUTH VALUE OF A CONDITIONAL Is the conditional true or false. If it is false, find a counterexample. A. If a woman is Pennsylvanian then she is American. B. If a number is divisible by 3, then it is odd.

NEGATION The negation of a statement p is the opposite of the statement. The symbol is ~p and is read “_____”. Ex. You can use negations to write statements related to a conditional.

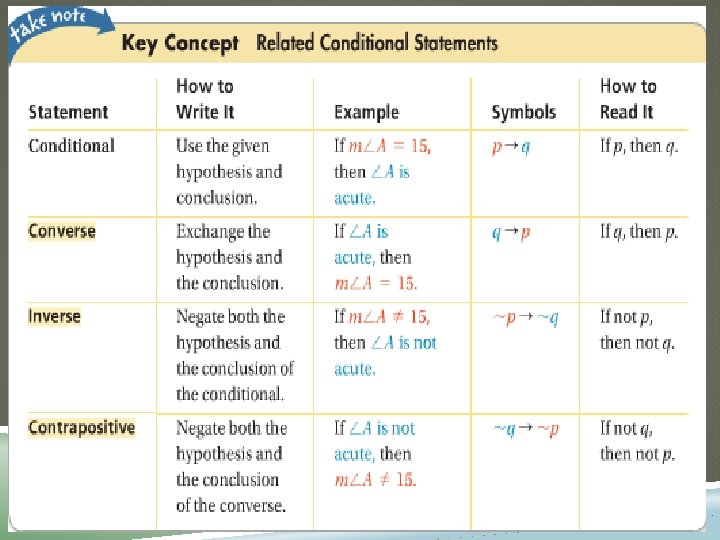
EQUIVALENT STATEMENTS Equivalent statements have_________ Conditional and contrapositive – They are either both true or both false. Converse and inverse –

WRITING AND FINDING TRUTH VALUES OF STATEMENTS What are the converse, inverse, and contrapositive of the following conditional. What are the truth values of each? If a statement is false, give a counterexample. If the figure is a square, then the figure is a quadrilateral.