2 1 Six Trig Functions for Right Triangles

2. 1 Six Trig Functions for Right Triangles sin ( ) = Opposite csc ( ) = Hypotenuse Opposite cos ( ) = Adjacent sec ( ) = Hypotenuse [secant] Adjacent tan ( ) = Opposite cot( ) = Adjacent Opposite Note: is an Acute angle. 12 [cosecant] 13 5 [cotangent] sin ( ) = 12 13 csc( ) = 13 12 cos( ) = 5 13 sec( ) = 13 5 tan( ) = 12 / 5 cot( ) = 5 / 12

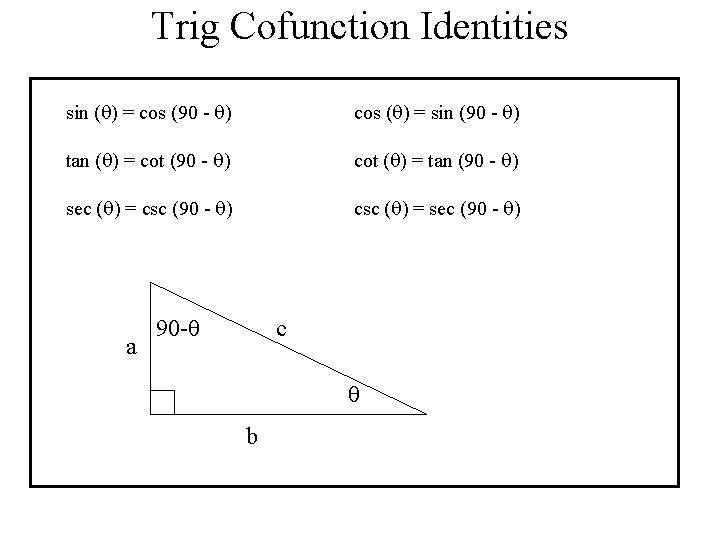
Trig Cofunction Identities sin ( ) = cos (90 - ) cos ( ) = sin (90 - ) tan ( ) = cot (90 - ) cot ( ) = tan (90 - ) sec ( ) = csc (90 - ) csc ( ) = sec (90 - ) a 90 - c b

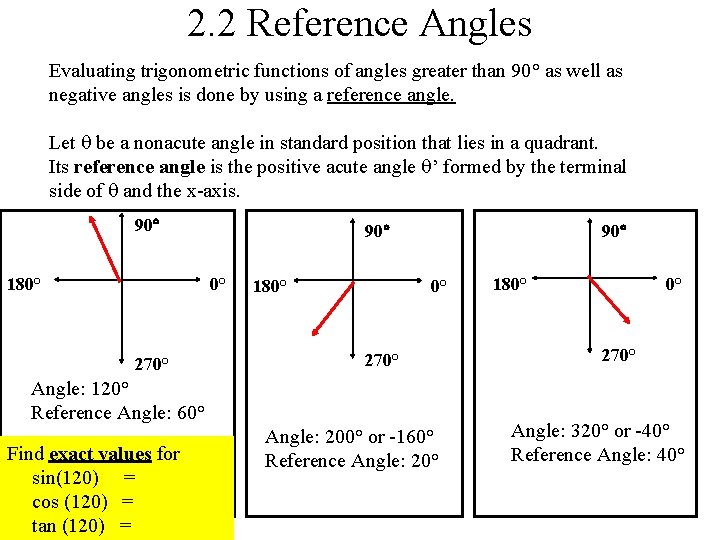
2. 2 Reference Angles Evaluating trigonometric functions of angles greater than 90° as well as negative angles is done by using a reference angle. Let be a nonacute angle in standard position that lies in a quadrant. Its reference angle is the positive acute angle ’ formed by the terminal side of and the x-axis. 90 180° 90 0° 270° Angle: 120° Reference Angle: 60° Find exact values for sin(120) = cos (120) = tan (120) = Angle: 200° or -160° Reference Angle: 20° 180° 0° 270° Angle: 320° or -40° Reference Angle: 40°

2. 3 Finding Trig Functions with Calculators • Make sure the calculator is in ‘DEGREE’ mode (Ti-83/84 – Use the ‘Mode’ Button) Examples: • Find sin (49º 12’) 12/60 =. 2 so, find sin (49. 2) =. 756995 2. Find sec (97. 977º) Secant is the reciprocal of cosine. Calculators do not have a ‘secant’ function so sec (97. 977) = 1/cos(97. 977) = -7. 205879 3. Sin =. 967709, Find Sin-1 (. 967709) = 74. 4º

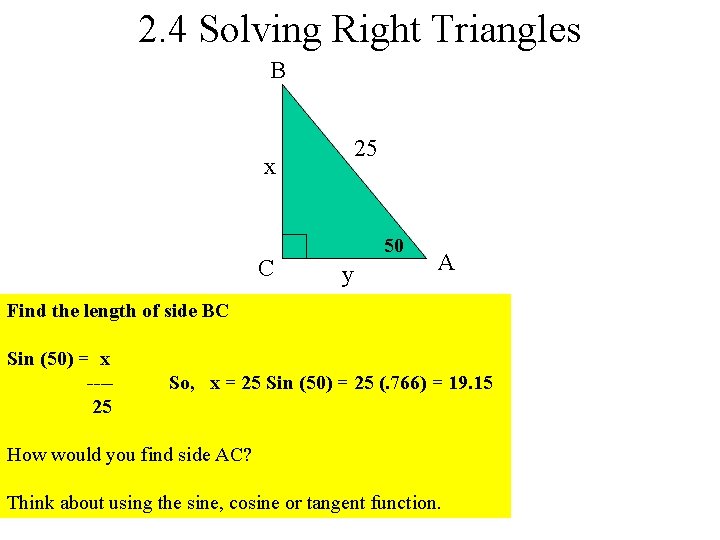
2. 4 Solving Right Triangles B 25 x C 50 y A Find the length of side BC Sin (50) = x ---25 So, x = 25 Sin (50) = 25 (. 766) = 19. 15 How would you find side AC? Think about using the sine, cosine or tangent function.

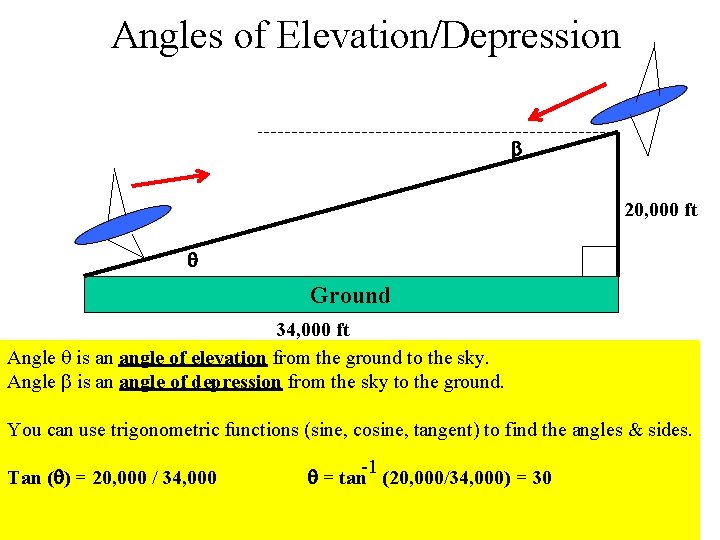
Angles of Elevation/Depression 20, 000 ft Ground 34, 000 ft Angle is an angle of elevation from the ground to the sky. Angle is an angle of depression from the sky to the ground. You can use trigonometric functions (sine, cosine, tangent) to find the angles & sides. Tan ( ) = 20, 000 / 34, 000 -1 = tan (20, 000/34, 000) = 30

2. 5 Bearing Application Problems Bearings are expressed using one of two methods: Method 1: (A single angle is given in degrees) 220º Method 2: (Directions and angle are given) S 40º W -- Measure the angle in a ‘clockwise’ direction from North -- Start with North/South Line -- Use an acute angle to show direction either east or west from the line. 220º 40º

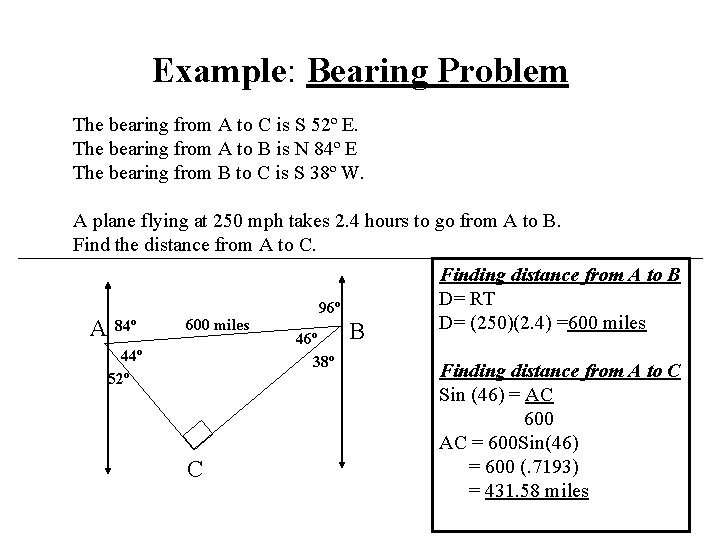
Example: Bearing Problem The bearing from A to C is S 52º E. The bearing from A to B is N 84º E The bearing from B to C is S 38º W. A plane flying at 250 mph takes 2. 4 hours to go from A to B. Find the distance from A to C. A 84º 600 miles 44º 52º C 96º 46º 38º B Finding distance from A to B D= RT D= (250)(2. 4) =600 miles Finding distance from A to C Sin (46) = AC 600 AC = 600 Sin(46) = 600 (. 7193) = 431. 58 miles