2 1 Relations and Functions Many every day

2. 1 Relations and Functions Many every day situations involve two quantities that are related in a certain way. In math we call this relationship a Relation. . Here are two examples 1. The simple interest I earned on an investment of $10, 000 for 1 year is related to the annual interest rate r by the formula I = 10, 000 r A Relation is any set of ordered pairs Example: { (2, 3), ( 4, 8), (6, 12)} 1

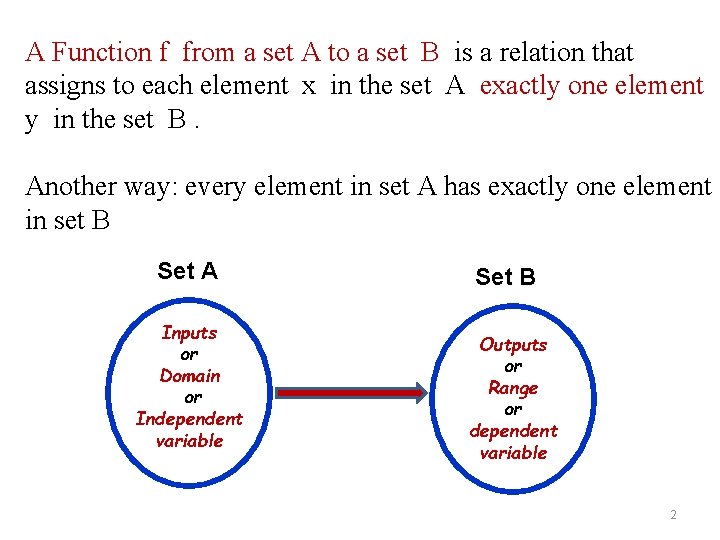
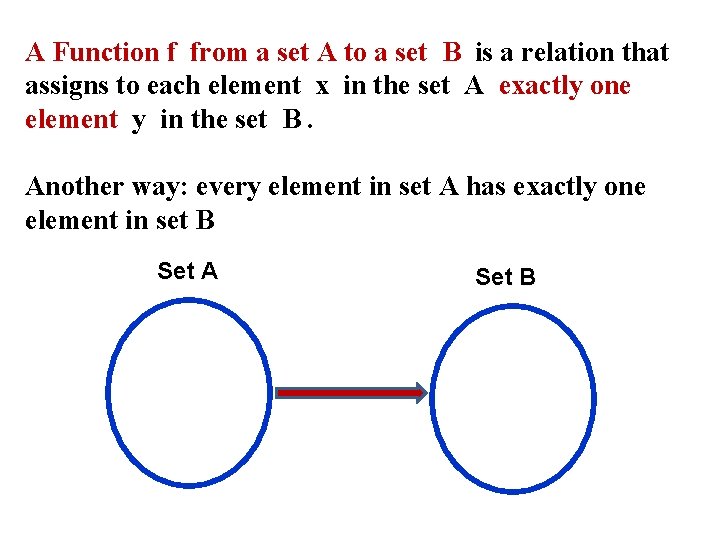
A Function f from a set A to a set B is a relation that assigns to each element x in the set A exactly one element y in the set B. Another way: every element in set A has exactly one element in set B Set A Inputs or Domain or Independent variable Set B Outputs or Range or dependent variable 2

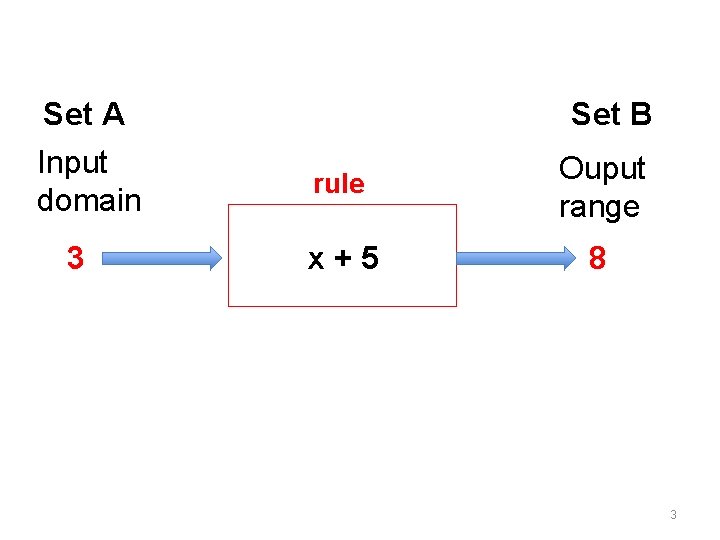
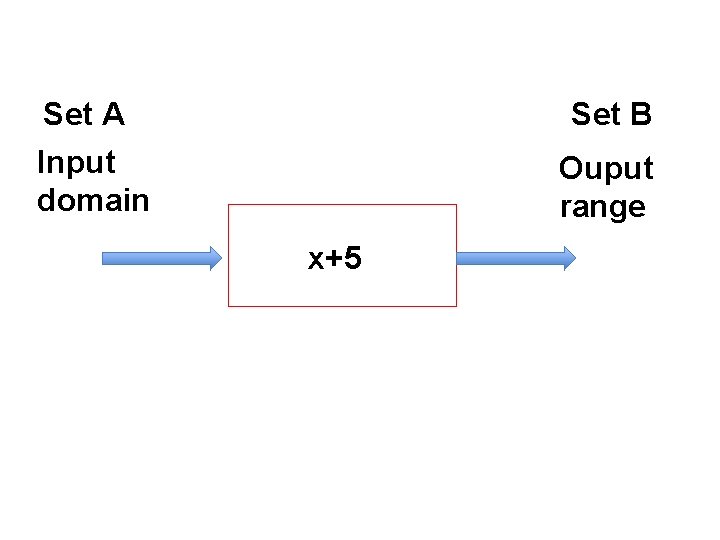
Set A Set B Input domain rule Ouput range x+5 8 3 3

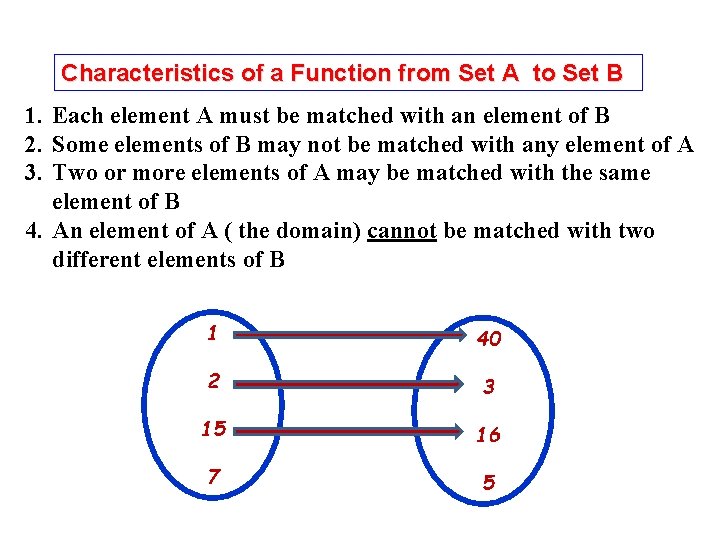
Characteristics of a Function from Set A to Set B 1. Each element A must be matched with an element of B 2. Some elements of B may not be matched with any element of A 3. Two or more elements of A may be matched with the same element of B 4. An element of A ( the domain) cannot be matched with two different elements of B 1 40 2 3 15 16 7 5 4

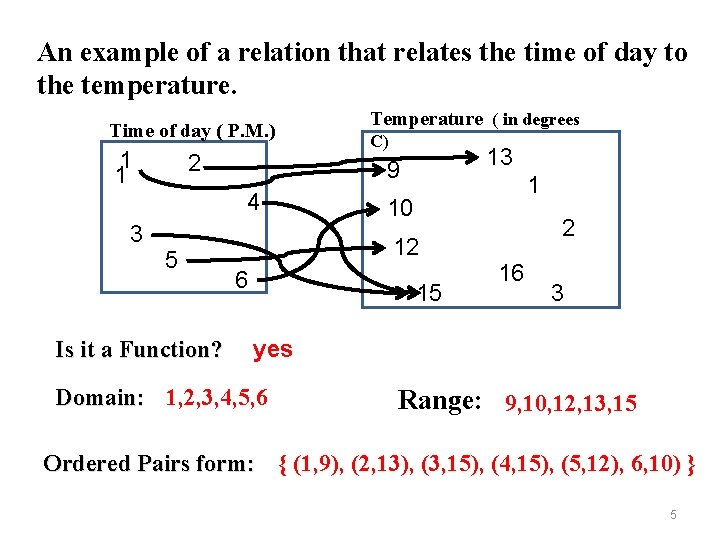
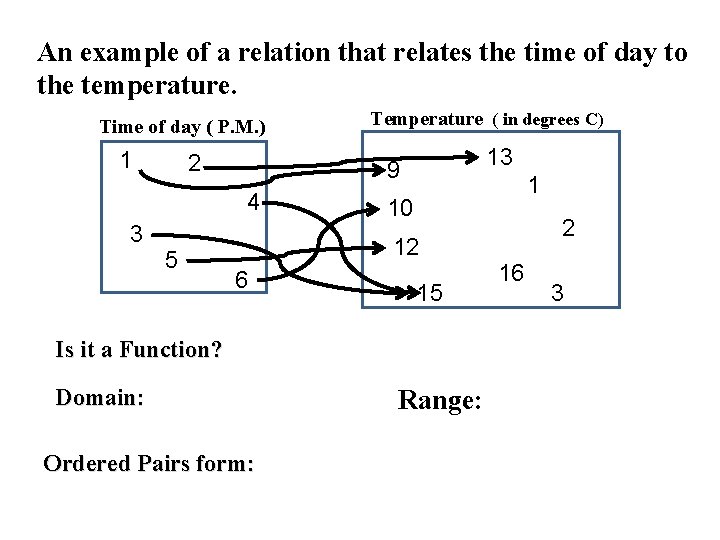
An example of a relation that relates the time of day to the temperature. Time of day ( P. M. ) 1 1 2 5 Is it a Function? C) 13 9 4 3 Temperature ( in degrees 1 10 12 6 15 2 16 3 yes Domain: 1, 2, 3, 4, 5, 6 Range: 9, 10, 12, 13, 15 Ordered Pairs form: { (1, 9), (2, 13), (3, 15), (4, 15), (5, 12), 6, 10) } 5

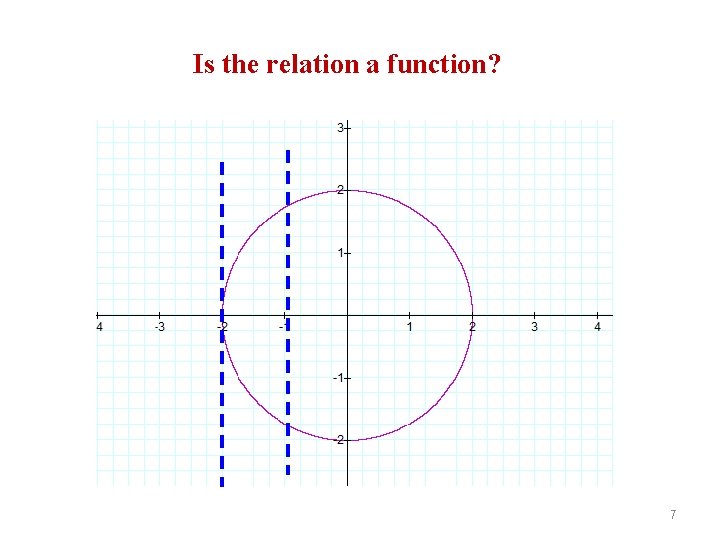
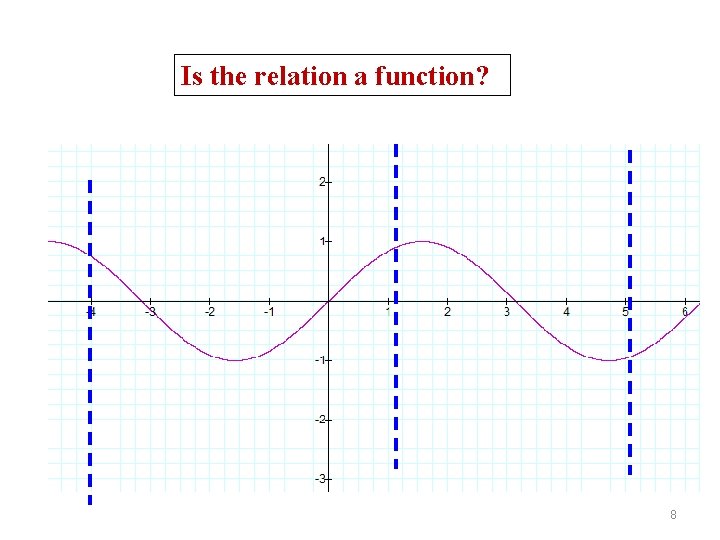
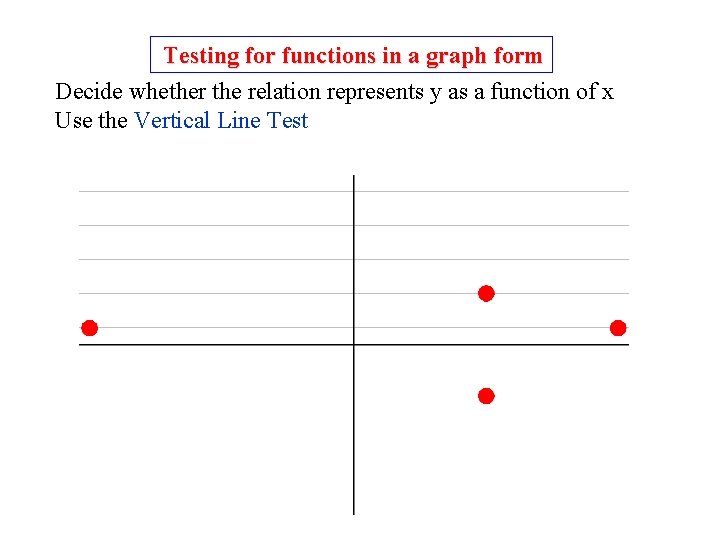
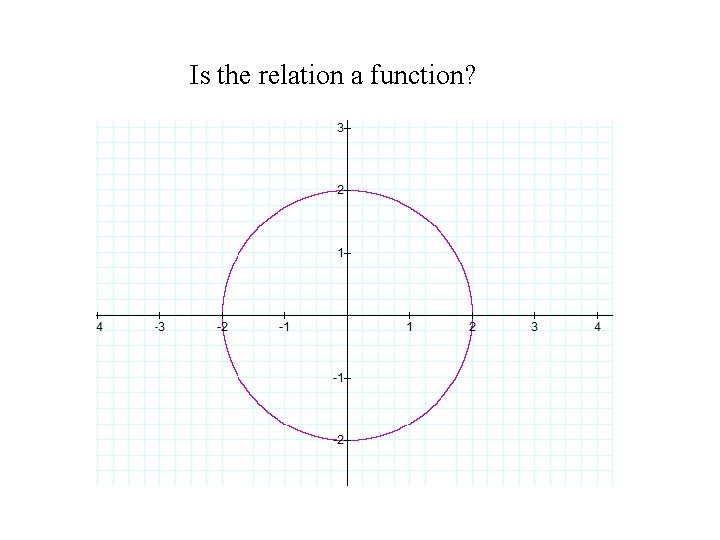
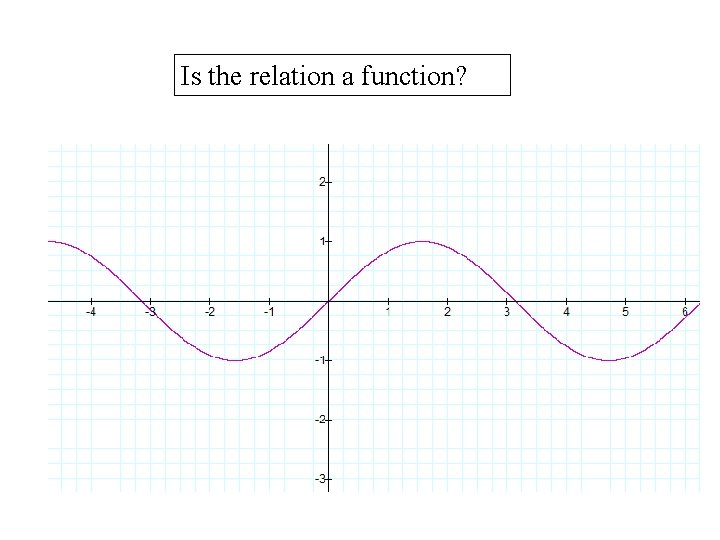
Testing for functions in a graph form Decide whether the relation represents y as a function of x Use the Vertical Line Test 6

Is the relation a function? 7

Is the relation a function? 8

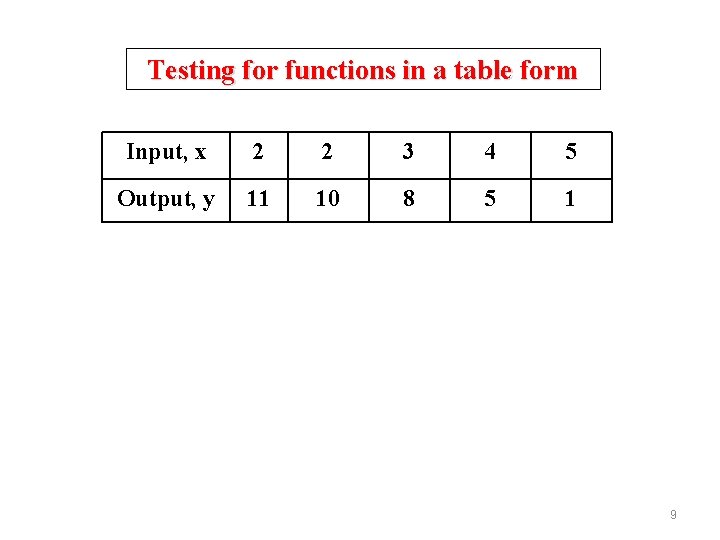
Testing for functions in a table form Input, x 2 2 3 4 5 Output, y 11 10 8 5 1 9

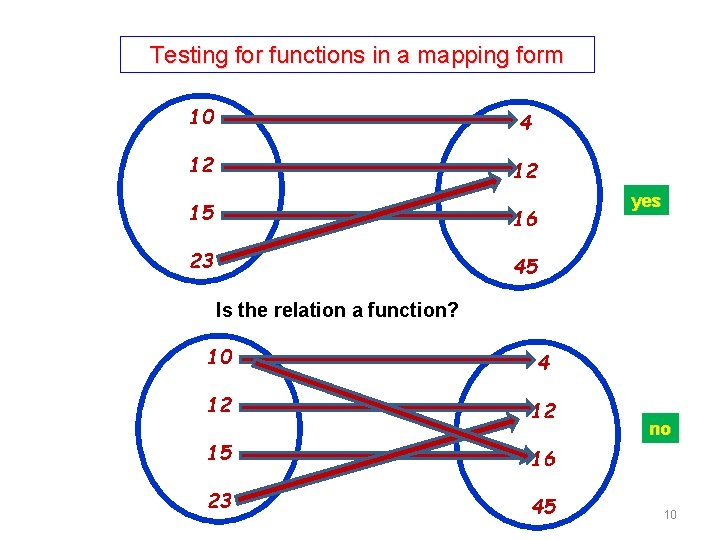
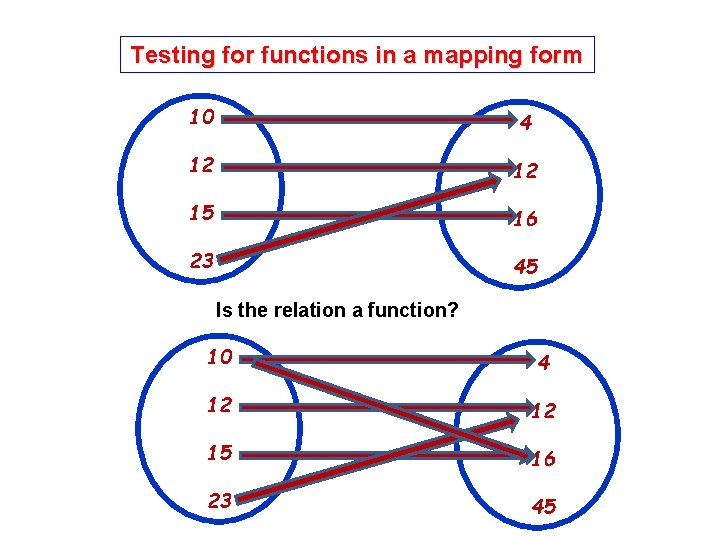
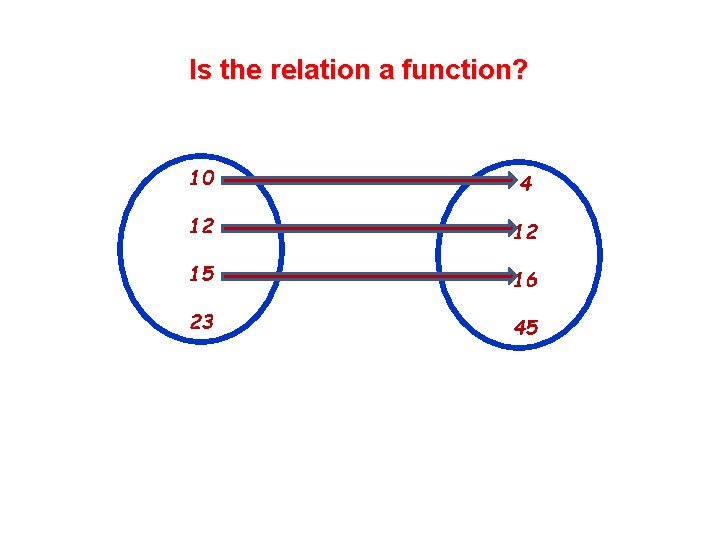
Testing for functions in a mapping form 10 4 12 12 15 16 23 45 yes Is the relation a function? 10 4 12 12 15 16 23 45 no 10

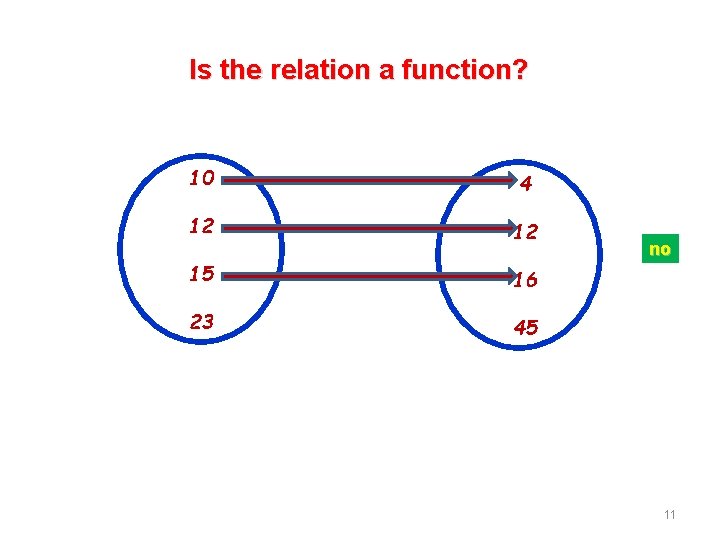
Is the relation a function? 10 4 12 12 15 16 23 45 no 11

Testing for Functions Represented Algebraically Decide whether the relation represents y as a function of x (solve for y) 12

Function Notation When an equation is used to represent a function, it is convenient to name the function so that it can be easily referenced. 13

Although f is often used as a function name and x as the independent variable, other letters can be used. Example. all represent the same function. The function could be written as 14

Evaluating functions 15

16

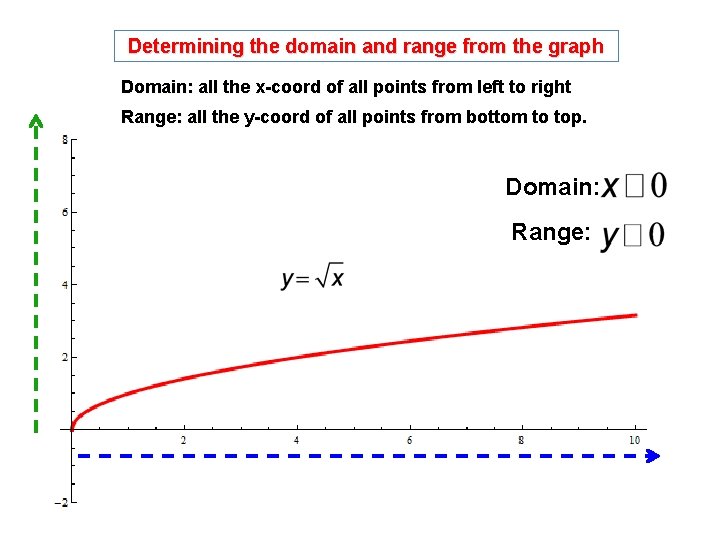
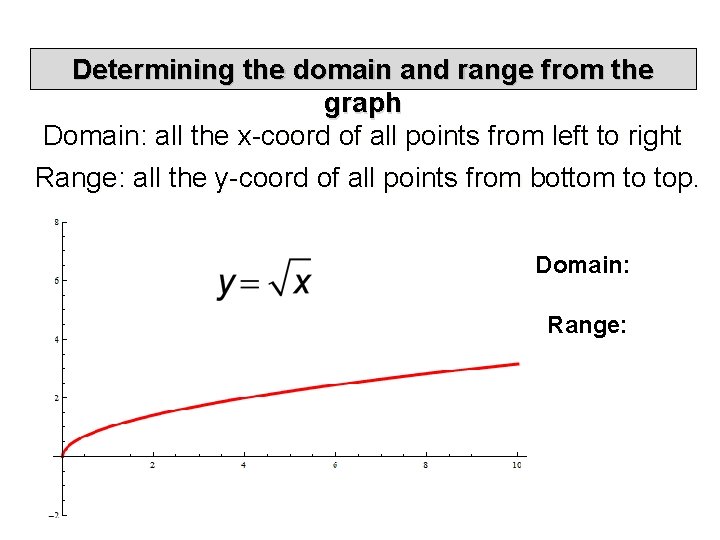
Determining the domain and range from the graph Domain: all the x-coord of all points from left to right Range: all the y-coord of all points from bottom to top. Domain: Range:

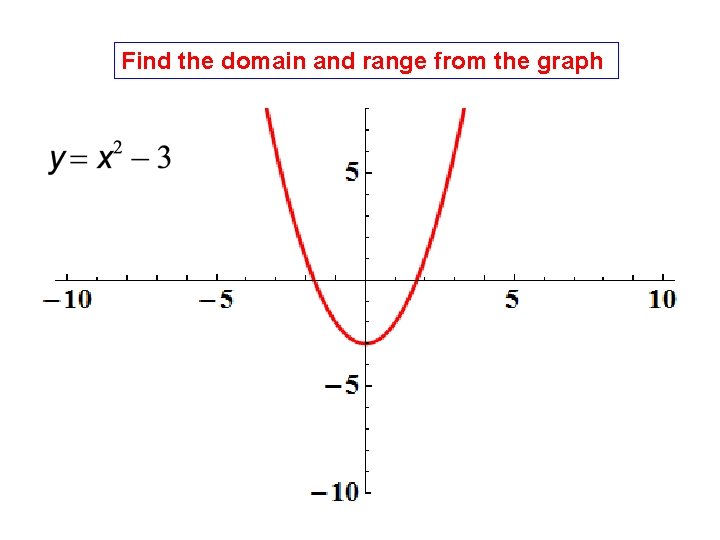
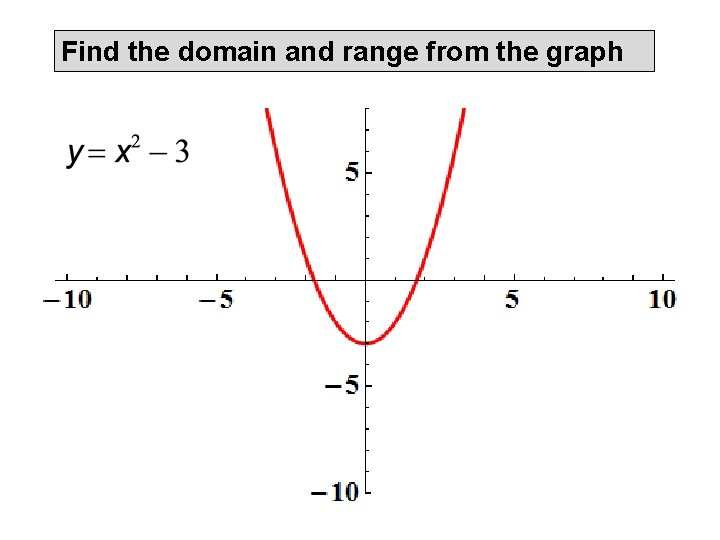
Find the domain and range from the graph

Determining the domain of a function from its equation The domain of a function can be described a. explicitly ( as in a piecewise function) b. implicitely by the expression used to define the function. The implied domain is the set of all real numbers for which the expression is defined. To find the domain of a function you need to exclude values that will : a. b. cause division by zero result in an even root of a negative number.

Find the implied domain of each function by analyzing the given equation

Find the domain of each function

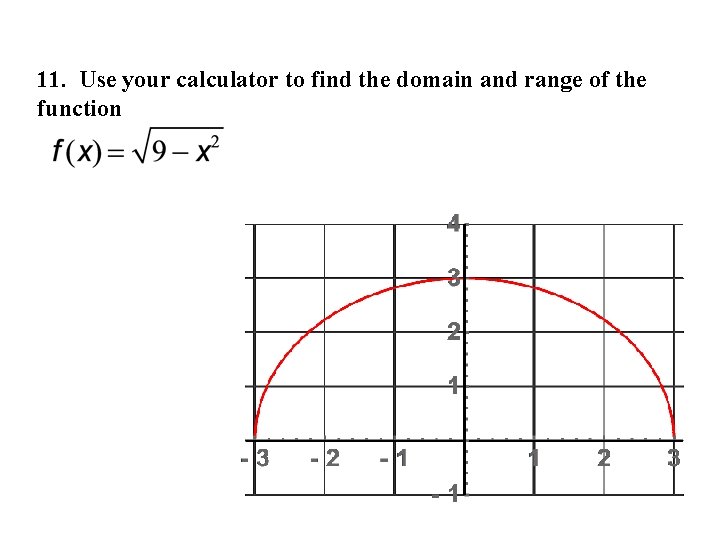
11. Use your calculator to find the domain and range of the function

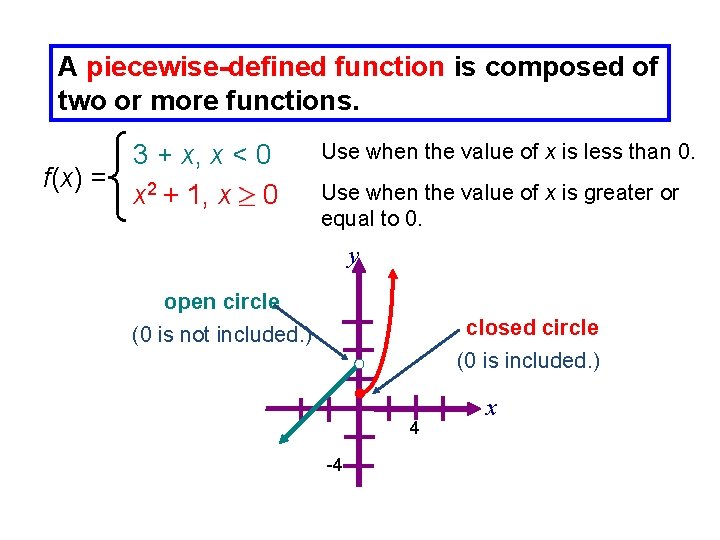
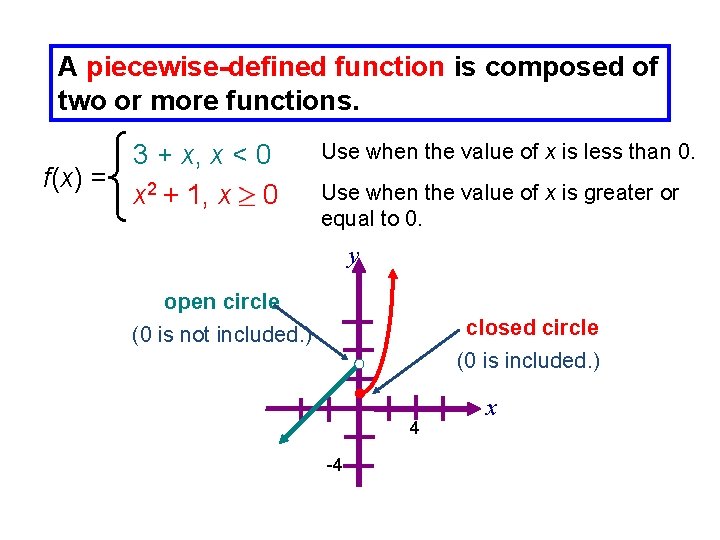
A piecewise-defined function is composed of two or more functions. 3 + x, x < 0 f(x) = 2 x + 1, x 0 Use when the value of x is less than 0. Use when the value of x is greater or equal to 0. y open circle (0 is not included. ) closed circle (0 is included. ) 4 -4 x

Evaluating a Piecewise-Defined Function

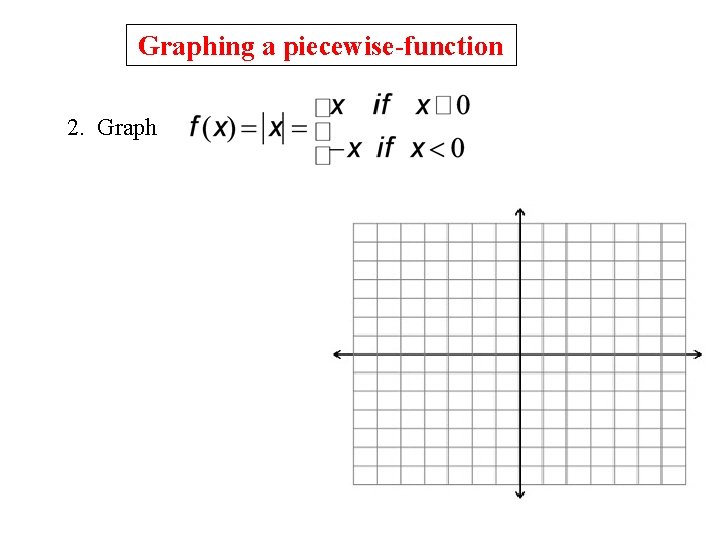
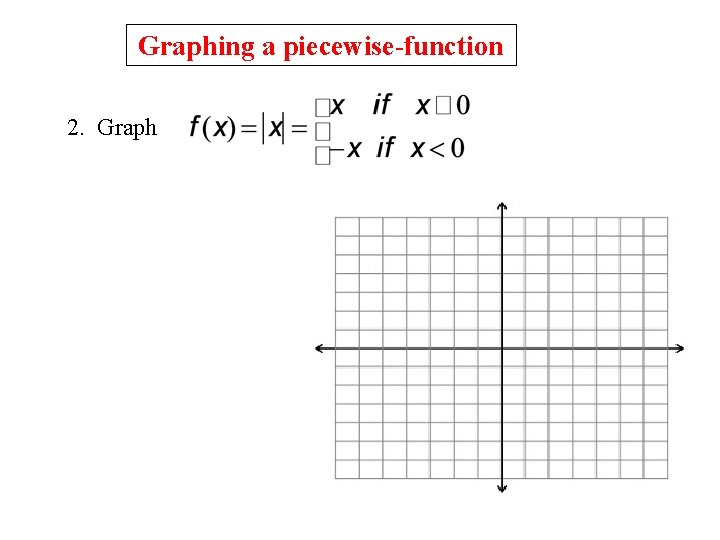
Graphing a piecewise-function 2. Graph

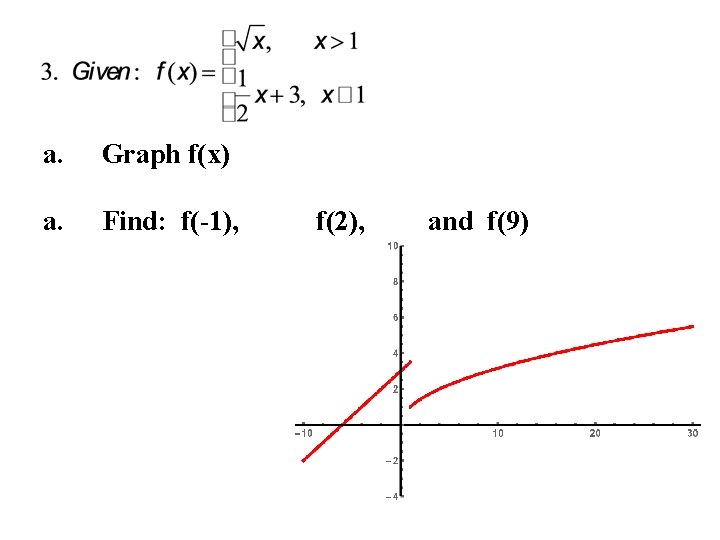
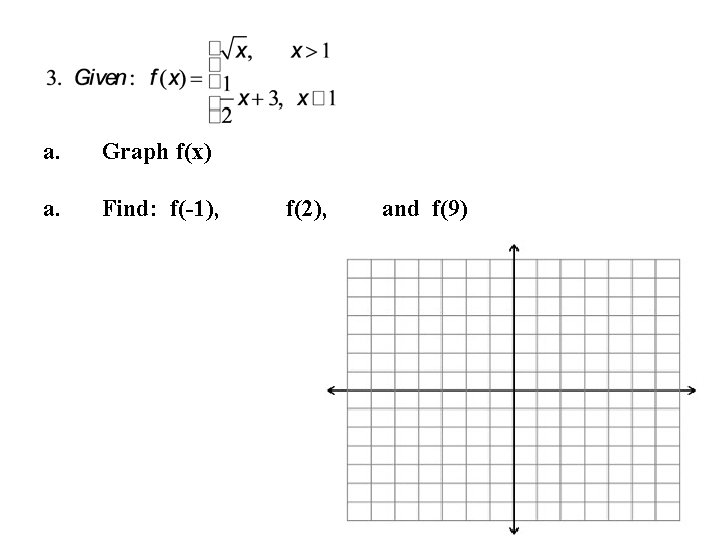
a. Graph f(x) a. Find: f(-1), f(2), and f(9)

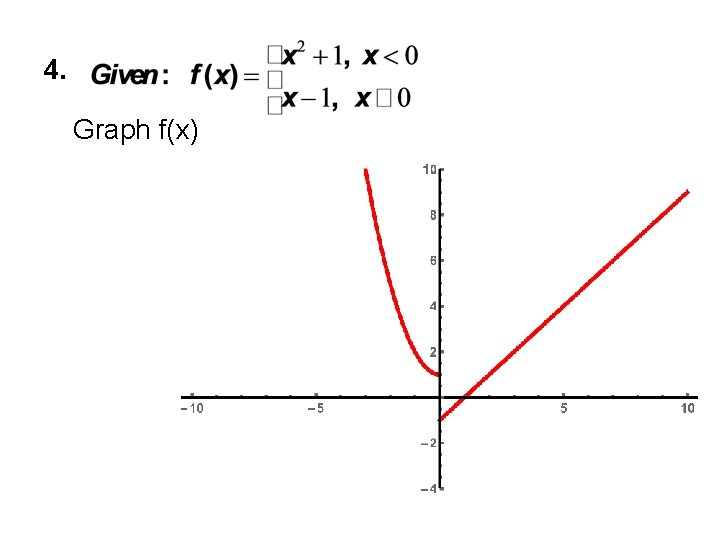
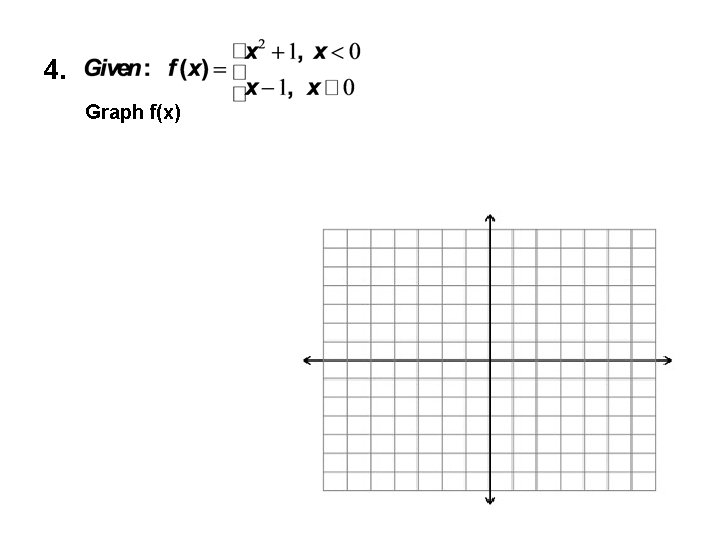
4. Graph f(x)

Handout

Relations and Functions Many every day situations involve two quantities that are related in a certain way. In math we call this relationship a Relation. Here are two examples A Relation is any set of ordered pairs Example: { (2, 3), ( 4, 8), (6, 12)}

A Function f from a set A to a set B is a relation that assigns to each element x in the set A exactly one element y in the set B. Another way: every element in set A has exactly one element in set B Set A Set B

Set A Set B Input domain Ouput range x+5

Characteristics of a Function from Set A to Set B 1. Each element A must be matched with an element of B 2. Some elements of B may not be matched with any element of A 3. Two or more elements of A may be matched with the same element of B 4. An element of A ( the domain) cannot be matched with two different elements of B 1 40 2 3 15 16 7 5

An example of a relation that relates the time of day to the temperature. Time of day ( P. M. ) 1 2 5 13 9 4 3 Temperature ( in degrees C) 1 10 12 6 15 Is it a Function? Domain: Ordered Pairs form: Range: 2 16 3

Testing for functions in a graph form Decide whether the relation represents y as a function of x Use the Vertical Line Test

Is the relation a function?

Is the relation a function?

Testing for functions in a table form Input, x 2 2 3 4 5 Output, y 11 10 8 5 1

Testing for functions in a mapping form 10 4 12 12 15 16 23 45 Is the relation a function? 10 4 12 12 15 16 23 45

Is the relation a function? 10 4 12 12 15 16 23 45

Testing for Functions Represented Algebraically Decide whether the relation represents y as a function of x (solve for y)

Function Notation When an equation is used to represent a function, it is convenient to name the function so that it can be easily referenced.

Although f is often used as a function name and x as the independent variable, other letters can be used. Example. all represent the same function. The function could be written as

Evaluating functions

Determining the domain and range from the graph Domain: all the x-coord of all points from left to right Range: all the y-coord of all points from bottom to top. Domain: Range:

Find the domain and range from the graph

Determining the domain of a function from its equation The domain of a function can be described a. explicitly ( as in a piecewise function) b. implicitely by the expression used to define the function. The implied domain is the set of all real numbers for which the expression is defined. To find the domain of a function you need to exclude values that will : a. cause division by zero b. result in an even root of a negative number.

Find the implied domain of each function by analyzing the given equation

Find the domain of each function

11. Use your calculator to find the domain and range of the function

A piecewise-defined function is composed of two or more functions. 3 + x, x < 0 f(x) = 2 x + 1, x 0 Use when the value of x is less than 0. Use when the value of x is greater or equal to 0. y open circle (0 is not included. ) closed circle (0 is included. ) 4 -4 x

Evaluating a Piecewise-Defined Function

Graphing a piecewise-function 2. Graph

a. Graph f(x) a. Find: f(-1), f(2), and f(9)

4. Graph f(x)