2 1 Reasoning and Logic An Introduction Students



















- Slides: 21

2 -1 Reasoning and Logic: An Introduction Students will be able to understand explain • Quantifiers and their effects on statements. • Different forms of statements. • How to determine whether two statements are logically equivalent. • How to develop logical arguments. • How to determine whether an argument is valid. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 1

Definitions Statement – a sentence that is either true or false, but not both. Negation – a statement with the opposite truth value of the given statement. The negation of a true statement is a false statement. If p is true, then ~ p is false. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 2

Example 1 Negate each of the following statements: 1. 2 + 3 = 5 2+3≠ 5 2. A hexagon has six sides. A hexagon does not have six sides. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 3

Definitions Quantifier – words such as “all”, “some”, “every”, “there exists”, and “no” (or none). Universal quantifier – applies to every element in a set. “All”, “every”, and “no” are universal quantifiers. Existential quantifier – applies to one or more (or possibly every) element in a set. Some and “there exists at least one” are existential quantifiers. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 4

Example 2 Negate each of the following regardless of its truth value: a. All students like hamburgers. Some students do not like hamburgers. b. Some people like mathematics. No people like mathematics. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 5

Example 2 continued Negate each of the following regardless of its truth value: c. There exists a natural number n such that 3 n = 6. For all natural numbers n, 3 n ≠ 6. d. For all natural numbers n, 3 n = 3 n. There exists a natural number n such that 3 n ≠ 3 n. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 6

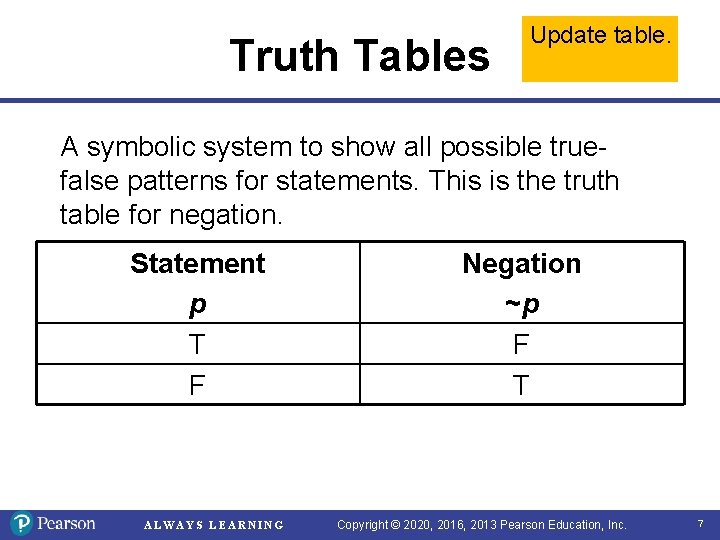
Truth Tables Update table. A symbolic system to show all possible truefalse patterns for statements. This is the truth table for negation. Statement p T F ALWAYS LEARNING Negation ~p F T Copyright © 2020, 2016, 2013 Pearson Education, Inc. 7

Conjunction A compound statement created from two given statements using the connective “and”. We use the symbol “ ” to represent “and”. A conjunction is true only if both statements are true; otherwise, it is false. p T T F F ALWAYS LEARNING q T F p q T F F F Copyright © 2020, 2016, 2013 Pearson Education, Inc. 8

Disjunction A compound statement created from two given statements using the connective “or”. We use the symbol “ ” to represent “or”. A disjunction is false if both statements are false and true in all other cases. p T T F F q T F ALWAYS LEARNING p q T T T F Copyright © 2020, 2016, 2013 Pearson Education, Inc. 9

Example 3 Classify each of the following as true or false: p: 2 + 3 = 5 q: 2 • 3 = 6 r: 5 + 3 = 9 a. p q p is true and q is true, so p q is true. b. q r q is true and r is false, so q r is true. c. ~p r ~p is false and r is false, so ~p r is false. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 10

Example 3 (continued) Classify each of the following as true or false: p: 2 + 3 = 5 q: 2 • 3 = 6 r: 5 + 3 = 9 d. ~p ~q ~p is false and ~q is false, so ~p ~q is false. e. ~(p q) p q is true, so ~(p q) is false. f. (p q) ~r p q is true and ~r is true, so (p q) ~r is true. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 11

Conditionals and Biconditionals Conditional (or implication) – a statement expressed in the form “if p, then q. ” Represented by p →q. p T T F F q T F p→q T F T T Hypothesis – the “if” part of the conditional Conclusion – the “then” part of the conditional ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 12

Any implication p → q has three related implication statements: Statement If p, then q. p→q Converse If q, then p. q→p Inverse If not p, then not q. ~p → ~ q Contrapositive If not q, then not p. ~q → ~ p ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 13

Example 6 Write the converse, inverse, and contrapositive for the following statement: If I am in San Francisco, then I am in California. Converse: If I am in California, then I am in San Francisco. Inverse: If I am not in San Francisco, then I am not in California. Contrapositive: If I am not in California, then I am not in San Francisco. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 14

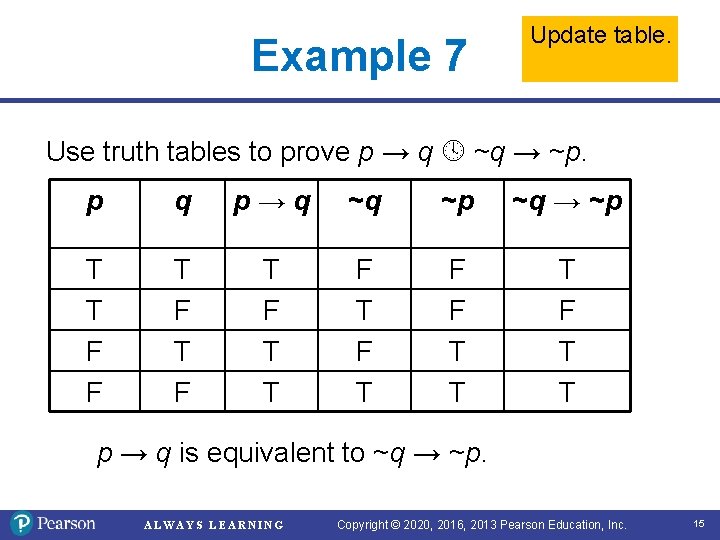
Example 7 Update table. Use truth tables to prove p → q ~q → ~p. p q p→q ~q ~p ~q → ~p T T F F T F T F F T T T F T T p → q is equivalent to ~q → ~p. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 15

Biconditional The conjunction of a statement and its converse. It is written as p ↔ q and is read “p if and only if q. ” p q p→q T T F F T F T T ALWAYS LEARNING q → p (p → q) (q → p) T T F F T Copyright © 2020, 2016, 2013 Pearson Education, Inc. 16

Valid reasoning – if the conclusion follows unavoidably from true hypotheses. Example Hypotheses: Conclusion: ALWAYS LEARNING All cats like fish. Felix is a cat. Therefore, Felix likes fish. Copyright © 2020, 2016, 2013 Pearson Education, Inc. 17

We can use an Euler diagram to represent the validity of this reasoning. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 18

Example 8 Determine if the following argument is valid: Hypotheses: In Washington, D. C. , all lobbyists have influence. No one in Washington, D. C. , over 6 ft tall has influence. Conclusion: Persons over 6 ft tall are not lobbyists in Washington, D. C. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 19

Example 8 (continued) We can use an Euler diagram to represent the validity of this reasoning. I ALWAYS LEARNING I Copyright © 2020, 2016, 2013 Pearson Education, Inc. 20

Example 8 (continued) I I If L represents the lobbyists in Washington, D. C. , and I the people who have influence, the first hypothesis is pictured on the left. If W represents the people in Washington, D. C. , over 6 ft tall, the second hypothesis is pictured on the right. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 21