2 1 Power and Radical Functions Objective Graph

2. 1 – Power and Radical Functions Objective: Graph and analyze power & radical functions.

Vocab: •

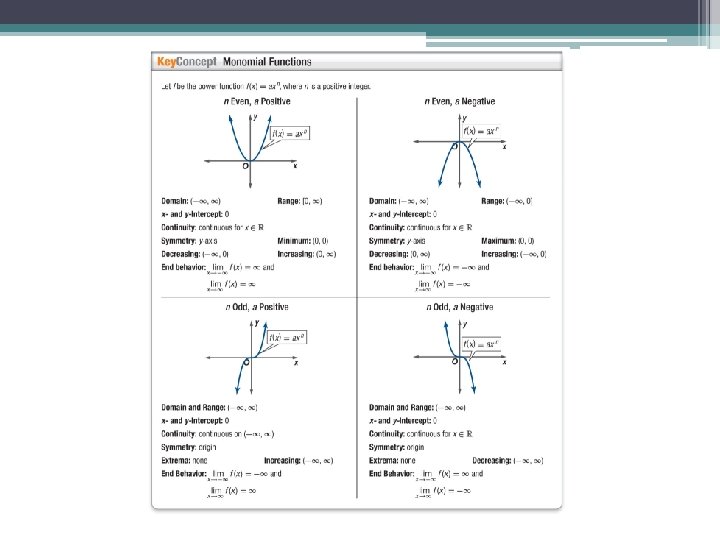
Example 1: Graph and analyze. Describe the domain, range, intercepts, end behavior, continuity, and where the function is increasing or decreasing.

Example 2: Graph and analyze f (x) = 2 x – 4. Describe the domain, range, intercepts, end behavior, continuity, and where the function is increasing or decreasing.

Example 3: Describe the end behavior of the graph of f (x) = 3 x – 5. A. B. C. D.

Example 4: Graph and analyze. Describe the domain, range, intercepts, end behavior, continuity, and where the function is increasing or decreasing.

Example 5: Graph and analyze. Describe the domain, range, intercepts, end behavior, continuity, and where the function is increasing or decreasing.

Example 6: Describe the continuity of the function A. B. C. D. continuous for all real numbers continuous on and continuous on (0, ∞] continuous on [0, ∞)

Radical Functions: • Even roots vs. Odd roots • How do we get the starting point when necessary?

Example 7: Graph and analyze. Describe the domain, range, intercepts, end behavior, continuity, and where the function is increasing or decreasing.

Example 8: Find the intercepts of the graph of

Warm-Up: Analyze f (x) = 3 x 3. A. D = (–∞, ∞) R = [0, ∞), intercept: 0, , continuous for all real numbers, decreasing: (–∞, 0) , increasing: (0, ∞) B. D = (–∞, ∞) R = (–∞, ∞), intercept: 0, , continuous for all real numbers, decreasing: (–∞, 0), increasing: (0, ∞) C. D = (–∞, ∞) R = (–∞, ∞), intercept: 0, , continuous for all real numbers, decreasing: (–∞, ∞) D. D = (–∞, ∞) R = (–∞, ∞), intercept: 0, continuous for all real numbers, increasing: (–∞, ∞) ,

Objective: Solve radical equations & inequalities. Solving Radical Equations ***Check for extraneous solutions!!!

Example 9: Solve:

Example 10: Solve:

Example 11: Solve:

Solving Radical Inequalities: ***Be careful with restrictions in the domain!!!

Example 12: •

Example 13: •

Exit Slip: Solve:

• Check to see that answer is in restriction. • If it’s not, you must use both inequalities in answer. • If so, answer to original inequality is only answer.