2 1 Patterns and Inductive Reasoning Objective Use

2 -1 Patterns and Inductive Reasoning Objective: Use inductive reasoning to make conjectures

• Inductive Reasoning based on patterns you observe. • Conjecture A conclusion you reach using inductive reasoning. Example A scientist dips a platinum wire into a solution containing salt (sodium chloride), passes the wire over a flame, and observes that it produces an orange-yellow flame. She does this with many other solutions that contain salt, finding that they all produce an orange-yellow flame. Conjecture If a solution contains sodium chloride, then in a flame test it produces an orange-yellow flame.

Example 2: Consider the sequence 2, 4, 7, 11, . . . Make a conjecture about the rule for generating the sequence. Then find the next three terms. Conjecture: You always add the next counting number to get the next term.

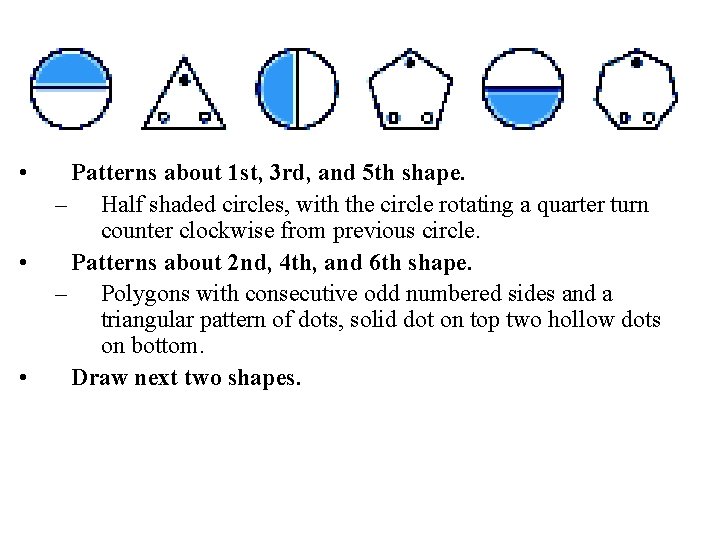
• • • Patterns about 1 st, 3 rd, and 5 th shape. – Half shaded circles, with the circle rotating a quarter turn counter clockwise from previous circle. Patterns about 2 nd, 4 th, and 6 th shape. – Polygons with consecutive odd numbered sides and a triangular pattern of dots, solid dot on top two hollow dots on bottom. Draw next two shapes.

Counterexample An example that shows that a conjecture is incorrect. Find one counterexample to prove a conjecture is false. If the name of a month starts with the letter J, it is a summer month. Counterexample: January starts with the letter J and it is a winter month.

What is a counterexample for each conjecture? • If a flower is red, it is a rose. • When you multiply a number by 3, the product is divisible by 6. p. 85: 7 -23 odd, 31 -39 odd