2 1 Inductive Reasoning and Conjecture Objectives Make

2. 1 Inductive Reasoning and Conjecture

Objectives Make conjectures based on inductive reasoning n Find counterexamples n

Making Conjectures n Conjecture – an educated guess n Inductive Reasoning – using observations to make a conjecture

Example 1: Make a conjecture about the next number based on the pattern. 2, 4, 12, 48, 240 Find a pattern: 2 4 × 2 12 × 3 48 × 4 240 × 5 The numbers are multiplied by 2, 3, 4, and 5. Conjecture: The next number will be multiplied by 6. So, it will be or 1440. Answer: 1440

Your Turn: Make a conjecture about the next number based on the pattern. Answer: The next number will be

Example 2: For points L, M, and N, and make a conjecture and draw a figure to illustrate your conjecture. Conjecture: L, M, and N are collinear. ,
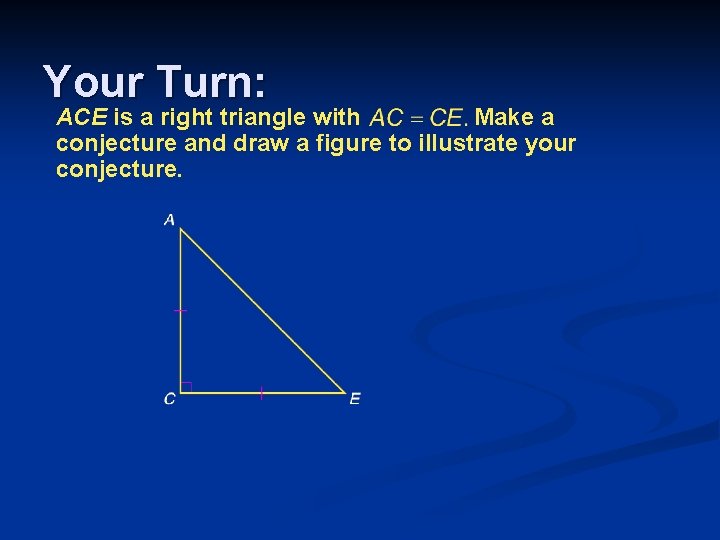
Your Turn: ACE is a right triangle with Make a conjecture and draw a figure to illustrate your conjecture.

Counterexamples n Providing evidence a conjecture false is a counterexample.
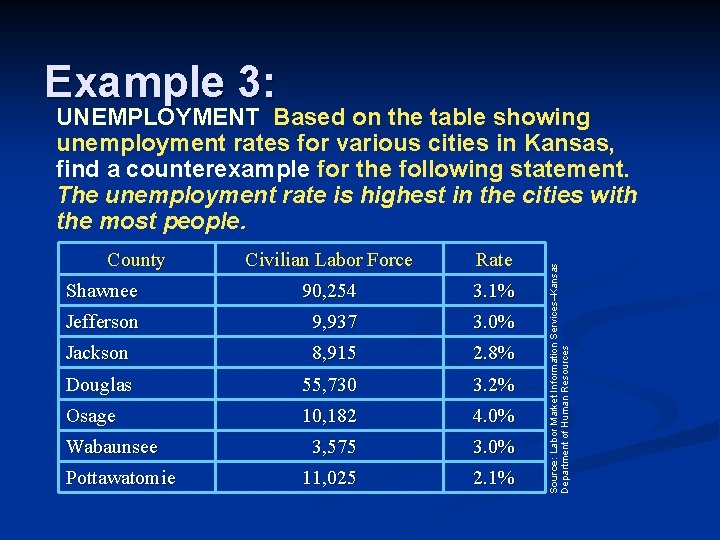
Example 3: County Civilian Labor Force Rate Shawnee 90, 254 3. 1% Jefferson 9, 937 3. 0% Jackson 8, 915 2. 8% Douglas 55, 730 3. 2% Osage 10, 182 4. 0% 3, 575 3. 0% 11, 025 2. 1% Wabaunsee Pottawatomie Source: Labor Market Information Services–Kansas Department of Human Resources UNEMPLOYMENT Based on the table showing unemployment rates for various cities in Kansas, find a counterexample for the following statement. The unemployment rate is highest in the cities with the most people.
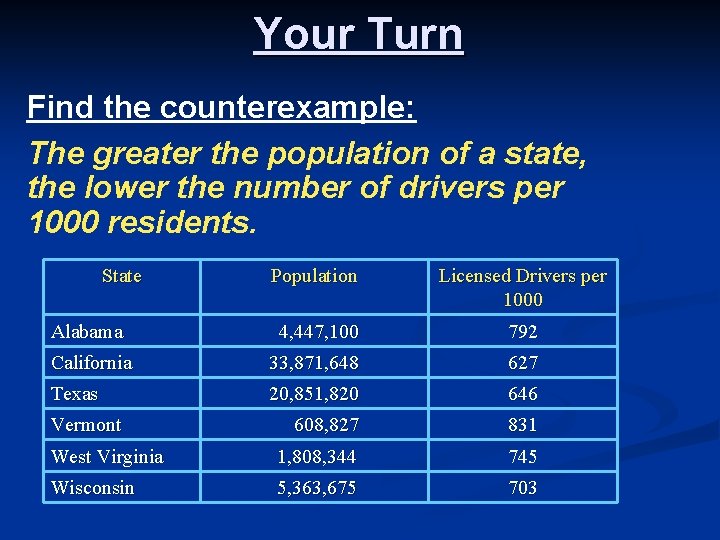
Your Turn Find the counterexample: The greater the population of a state, the lower the number of drivers per 1000 residents. State Population Licensed Drivers per 1000 Alabama 4, 447, 100 792 California 33, 871, 648 627 Texas 20, 851, 820 646 608, 827 831 West Virginia 1, 808, 344 745 Wisconsin 5, 363, 675 703 Vermont

Assignment n Geo WB, pgs. 20 -22
- Slides: 11