2 1 IfThen Statements Converses CONDITIONAL STATEMENTS are















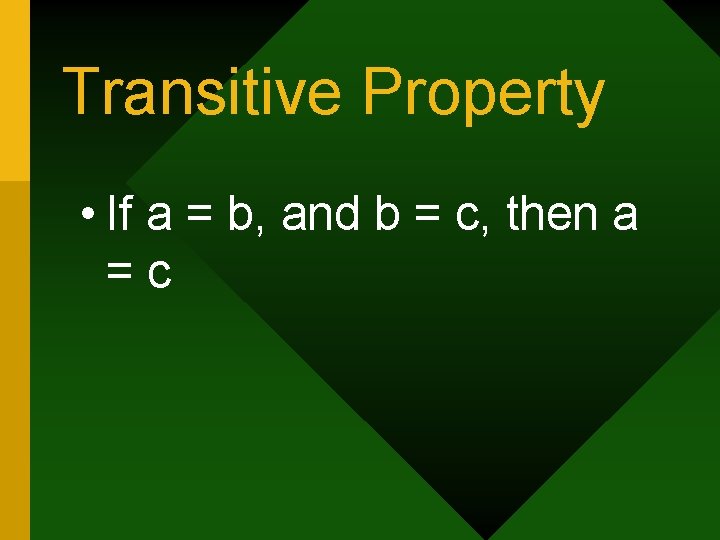


























- Slides: 43

2 -1 If-Then Statements; Converses

CONDITIONAL STATEMENTS are statements written in if-then form. The clause following the “if” is called the hypothesis and the clause following “then” is called the conclusion.

Examples • If it rains after school, then I will give you a ride home. • If you make an A on your test, then you will get an A on your report card.

CONVERSE is formed by interchanging the hypothesis and the conclusion.

Examples False Converses • If Bill lives in Texas, then he lives west of the Mississippi River. • If he lives west of the Mississippi River, then he lives in Texas

Counterexample • An example that shows a statement to be false • It only takes one counterexample to disprove a statement

Biconditional • A statement that contains the words “if and only if” • Segments are congruent if and only if their lengths are equal.

2 -2 Properties from Algebra

Addition Property • If a = b, and c = d, • then a + c = b + d

Subtraction Property • If a = b, and c = d, • then a - c = b - d

Multiplication Property • If a = b, • then ca = bc

Division Property • If a = b, and c 0 • then a/c = b/c

Substitution Property • If a = b, then either a or b may be substituted for the other in any equation (or inequality)

Reflexive Property • a = a

Symmetric Property • If a = b, then b = a
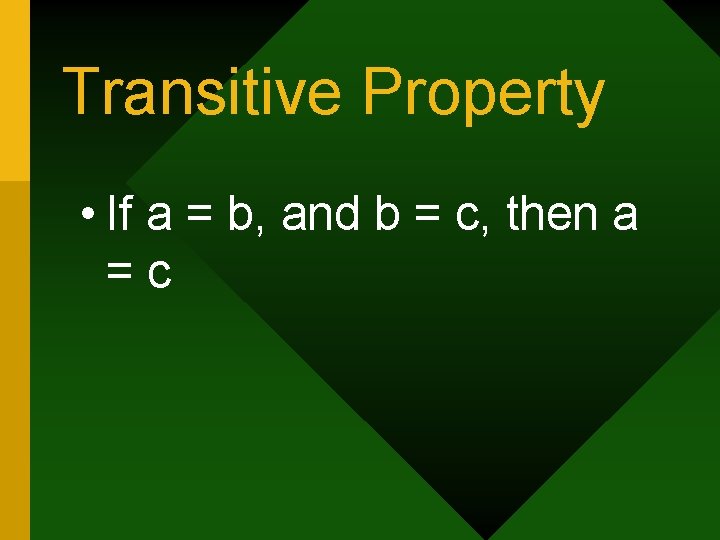
Transitive Property • If a = b, and b = c, then a =c

Distributive Property • a(b + c) = ab + ac

Properties of Congruence

Reflexive Property • DE • D D

Symmetric Property • If DE FG, then FG DE • If D E, then E D

Transitive Property • If DE FG, and FG JK, then DE JK • If D E, and E F, then D F

2 -3 Proving Theorems

Midpoint of a Segment – is the point that divides the segment into two congruent segments

THEOREM 2 -1 Midpoint Theorem If a point M is the midpoint of AB, then AM = ½AB and MB=½AB

BISECTOR of ANGLE– is the ray that divides the angle into two adjacent angles that have equal measure.

THEOREM 2 -2 Angle Bisector Theorem If BX is the bisector of ABC, then: m ABX = ½m ABC and m XBC = ½ m ABC


2 -4 Special Pairs of Angles

COMPLEMENTARY two angles whose measures have the sum 90º J 39º 51º K

SUPPLEMENTARY two angles whose measures have the sum 180º H 133º G 47º

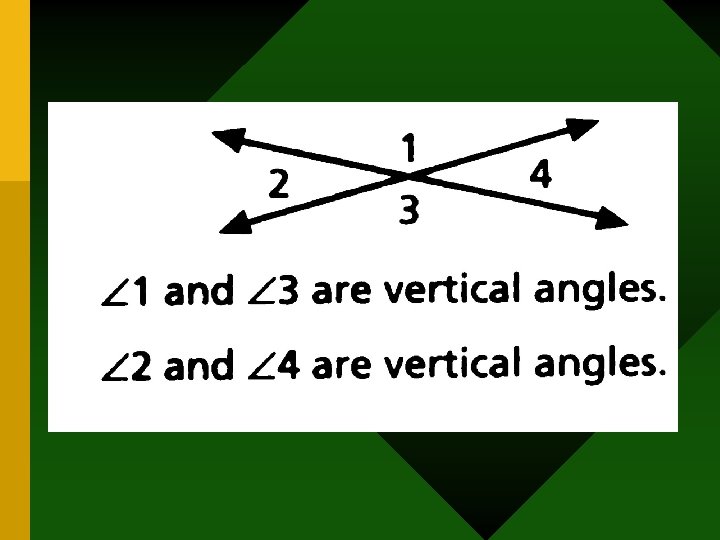
VERTICAL ANGLES– two angles whose sides form two pairs of opposite rays.


THEOREM 2 -3 Vertical angles are congruent

2 -5 Perpendicular Lines

Perpendicular Lines– two lines that intersect to form right angles ( 90° angles)

2 -4 THEOREM If two lines are perpendicular, then they form congruent adjacent angles.

2 -5 THEOREM If two lines form congruent adjacent angles, then the lines are perpendicular.

2 -6 THEOREM If the exterior sides of two adjacent acute angles are perpendicular, then the angles are complementary

2 -6 Planning a Proof

Parts of a Proof 1. A diagram that illustrates the given information 2. A list, in terms of the figure, of what is given 3. A list, in terms of the figure, of what you are to prove 4. A series of statements and reasons that lead from the given information to the statement that is to be proved

2 -7 THEOREM If two angles are supplements of congruent angles (or of the same angle), then the two angles are congruent.

2 -8 THEOREM If two angles are complements of congruent angles (or of the same angle), then the two angles are congruent.

THE END
 Mikael ferm
Mikael ferm Multiple incompatibility semantics
Multiple incompatibility semantics Delphi ifthen
Delphi ifthen Past unreal conditional
Past unreal conditional Conditional 4
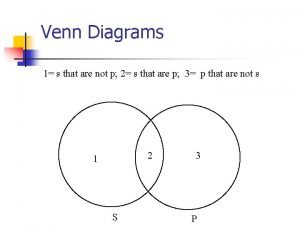
Conditional 4 Venn diagram conditional statement
Venn diagram conditional statement If you are a guitar player then you are a musician inverse
If you are a guitar player then you are a musician inverse Unit 2 homework 3 conditional statements
Unit 2 homework 3 conditional statements Conditional statement
Conditional statement Latin conditional sentences
Latin conditional sentences 2-2 practice conditional statements
2-2 practice conditional statements Flowchart do while
Flowchart do while 2-2 conditional statements
2-2 conditional statements Lesson 2-2 conditional statements
Lesson 2-2 conditional statements Conditional statement definition geometry
Conditional statement definition geometry Unit 3 lesson 1 conditional statements
Unit 3 lesson 1 conditional statements Arduino conditional statements
Arduino conditional statements Conditional and iterative statements
Conditional and iterative statements Conditional statement definition
Conditional statement definition Nested conditional statements
Nested conditional statements Conditional statement geometry definition
Conditional statement geometry definition 2-2 conditional statements
2-2 conditional statements Unit 2 homework 3 conditional statements
Unit 2 homework 3 conditional statements Biconditional statement in java
Biconditional statement in java Conditional statements examples
Conditional statements examples Unit 2 logic and proof homework 3 conditional statements
Unit 2 logic and proof homework 3 conditional statements Conditional statements matlab
Conditional statements matlab First conditional time clauses
First conditional time clauses Conditional statements definition
Conditional statements definition Converse geometry definition
Converse geometry definition 1conditional
1conditional Contoh conditional probability
Contoh conditional probability Venn diagram probability
Venn diagram probability Conditionals and biconditionals
Conditionals and biconditionals If conditional type 1
If conditional type 1 Conditional probability
Conditional probability Iterated conditional modes
Iterated conditional modes Onditional sentences
Onditional sentences Impossible conditional sentences
Impossible conditional sentences Future tense endings
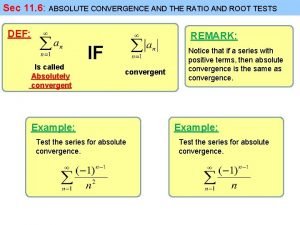
Future tense endings Ratio test
Ratio test 1 кондишинал
1 кондишинал Conditional probability with venn diagrams
Conditional probability with venn diagrams Four types of conditional sentences
Four types of conditional sentences