2 1 Functions and Their Graphs In this




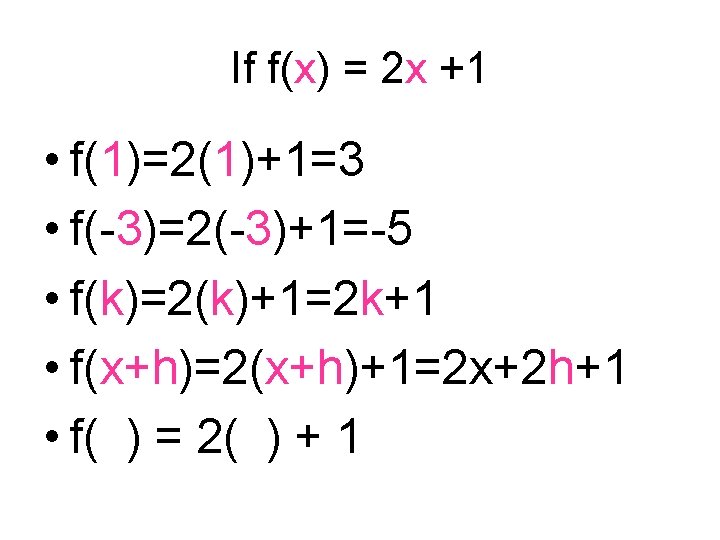









- Slides: 28

2. 1 Functions and Their Graphs

In this lesson you will: • Represent relations and functions. • Graph and evaluate linear functions.

Warm Up

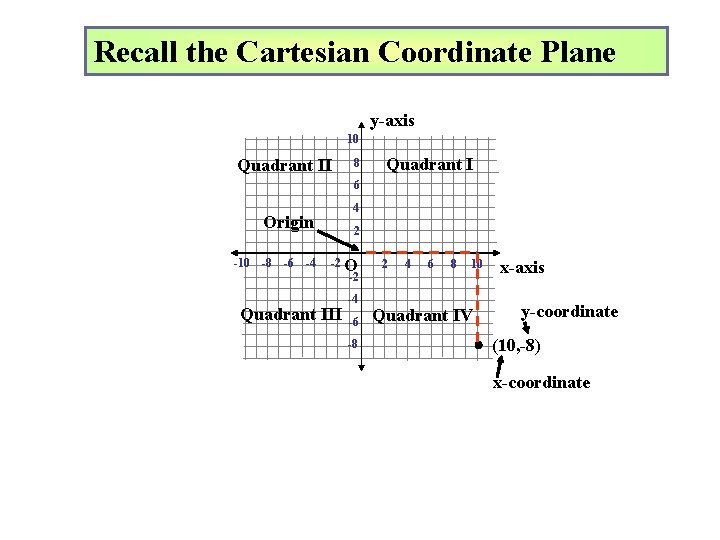
Recall the Cartesian Coordinate Plane y-axis 10 Quadrant II 8 Quadrant I 6 4 Origin -10 -8 -6 -4 2 -2 O -2 Quadrant III -4 -6 -8 2 4 6 8 10 Quadrant IV x-axis y-coordinate (10, -8) x-coordinate

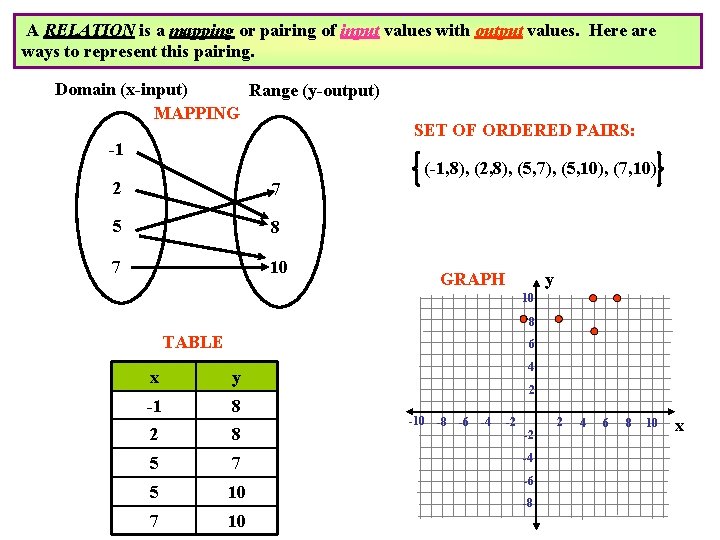
A RELATION is a mapping or pairing of input values with output values. Here are ways to represent this pairing. Domain (x-input) Range (y-output) MAPPING -1 SET OF ORDERED PAIRS: (-1, 8), (2, 8), (5, 7), (5, 10), (7, 10) 2 7 5 8 7 10 GRAPH y 10 8 TABLE 6 x y -1 8 2 8 5 7 5 10 7 10 4 2 -10 -8 -6 -4 -2 -2 -4 -6 -8 2 4 6 8 10 x

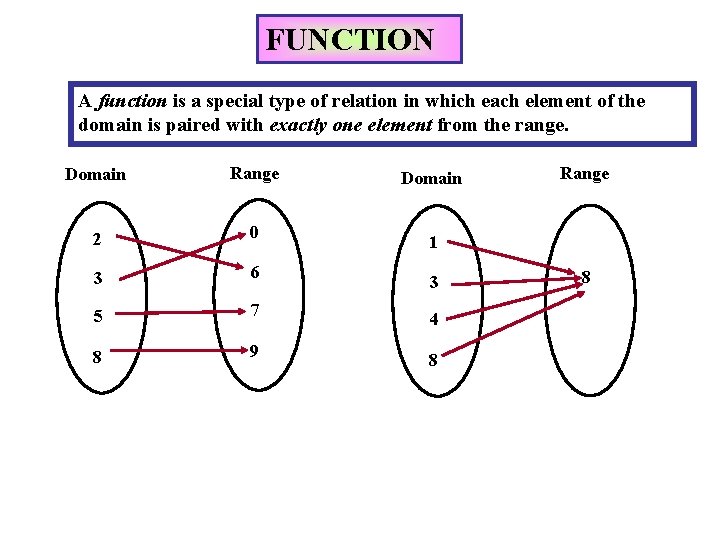
FUNCTION A function is a special type of relation in which each element of the domain is paired with exactly one element from the range. Domain Range 2 0 3 6 5 7 8 9 Domain Range 1 3 4 8 8

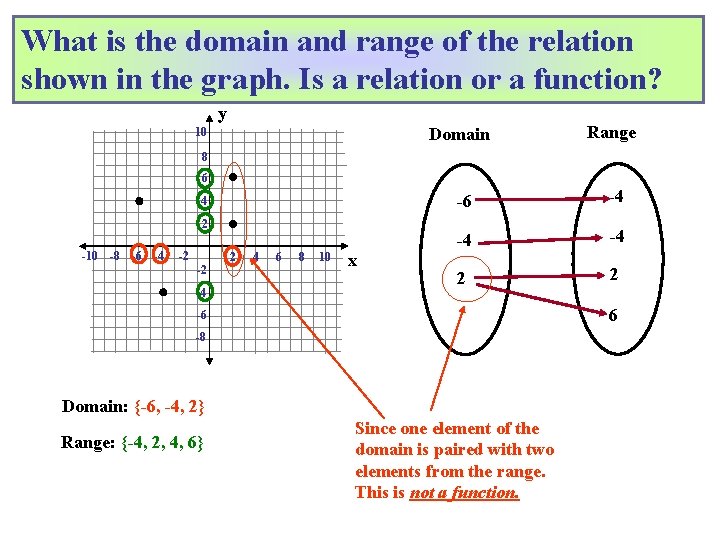
What is the domain and range of the relation shown in the graph. Is a relation or a function? y 10 Domain Range -6 -4 -4 -4 2 2 8 6 4 2 -10 -8 -6 -4 -2 -2 -4 2 4 6 8 10 x 6 -6 -8 Domain: {-6, -4, 2} Range: {-4, 2, 4, 6} Since one element of the domain is paired with two elements from the range. This is not a function.

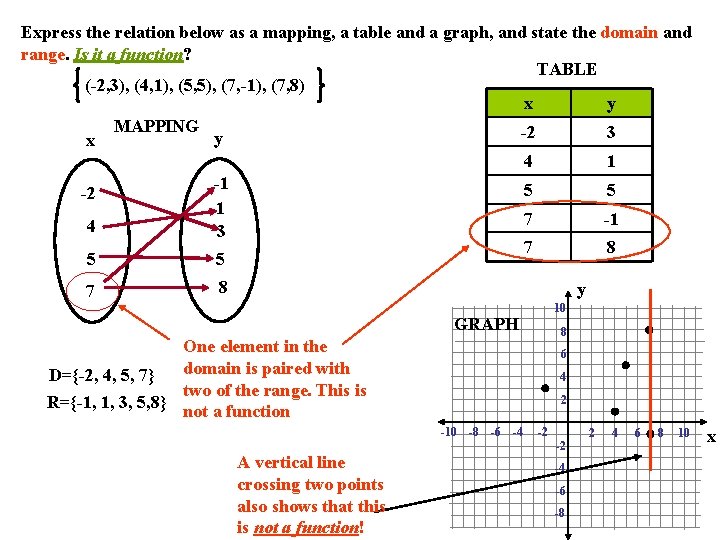
Express the relation below as a mapping, a table and a graph, and state the domain and range. Is it a function? TABLE (-2, 3), (4, 1), (5, 5), (7, -1), (7, 8) x y MAPPING -2 3 y x 4 1 -1 5 5 -2 1 7 -1 4 3 7 8 5 5 7 8 y 10 GRAPH 8 One element in the domain is paired with D={-2, 4, 5, 7} two of the range. This is R={-1, 1, 3, 5, 8} not a function 6 4 2 -10 -8 -6 -4 -2 -2 A vertical line crossing two points also shows that this is not a function! -4 -6 -8 2 4 6 8 10 x

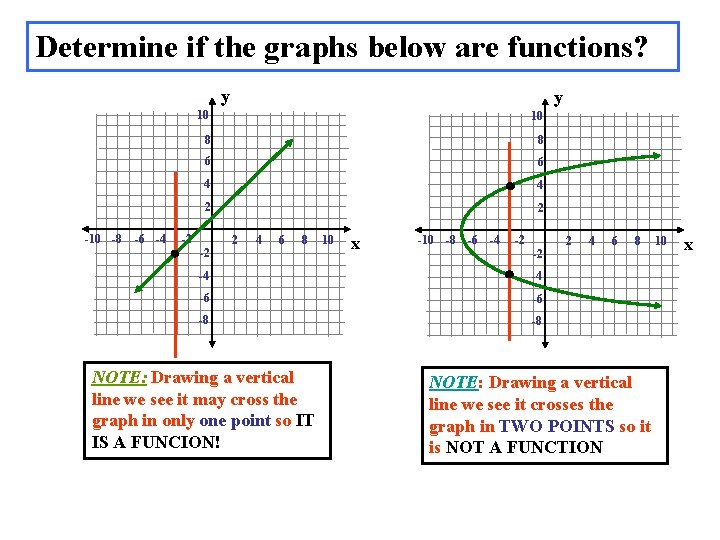
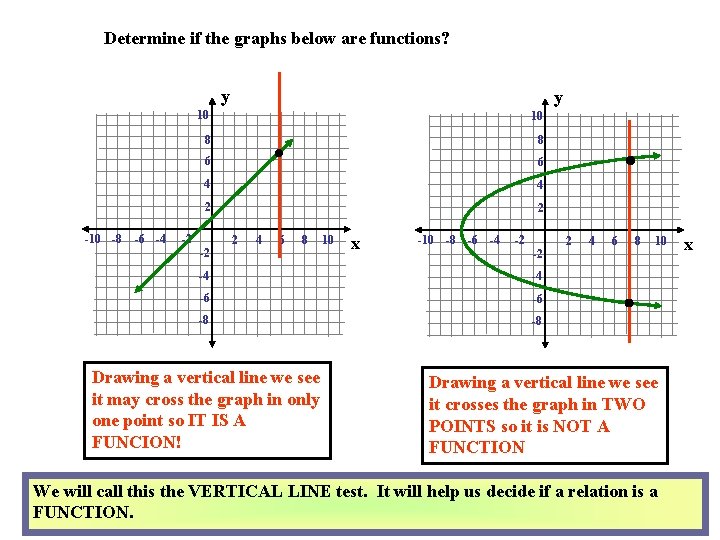
Determine if the graphs below are functions? y -10 -8 -6 -4 y 10 10 8 8 6 6 4 4 2 2 -2 -2 2 4 6 8 10 x -10 -8 -6 -4 -2 -2 2 4 6 8 -4 -4 -6 -6 -8 -8 NOTE: Drawing a vertical line we see it may cross the graph in only one point so IT IS A FUNCION! NOTE: Drawing a vertical line we see it crosses the graph in TWO POINTS so it is NOT A FUNCTION 10 x

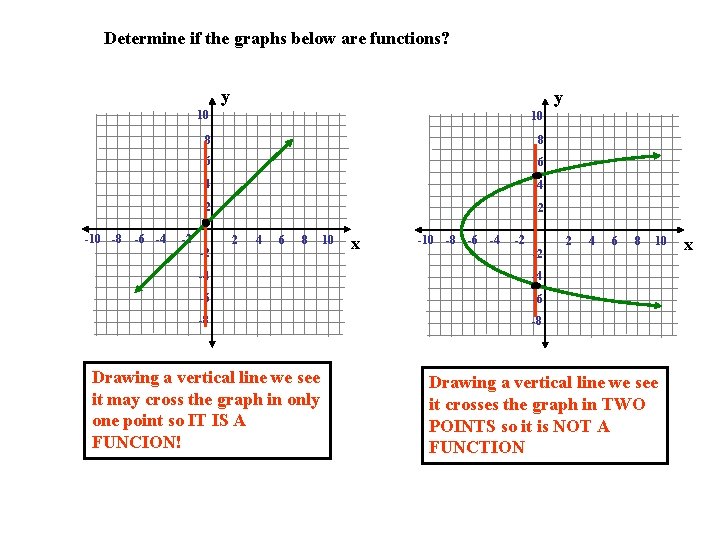
Determine if the graphs below are functions? y -10 -8 -6 -4 y 10 10 8 8 6 6 4 4 2 2 -2 -2 2 4 6 8 10 x -10 -8 -6 -4 -2 -2 -4 -4 -6 -6 -8 -8 Drawing a vertical line we see it may cross the graph in only one point so IT IS A FUNCION! 2 4 6 8 10 Drawing a vertical line we see it crosses the graph in TWO POINTS so it is NOT A FUNCTION x

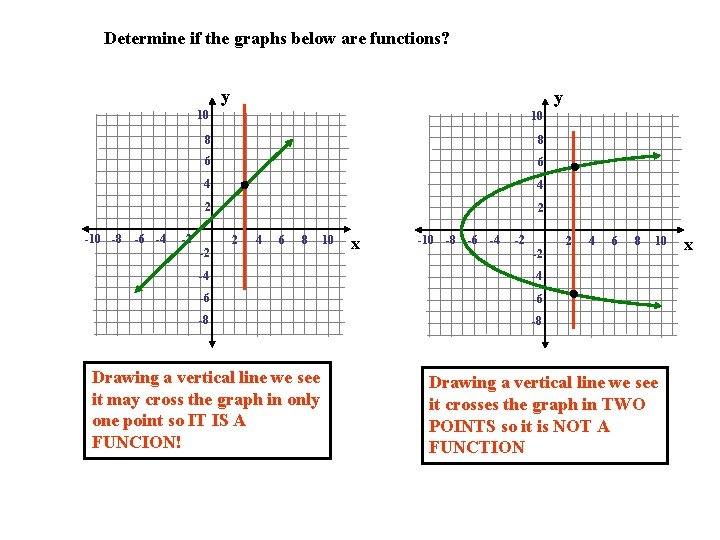
Determine if the graphs below are functions? y -10 -8 -6 -4 y 10 10 8 8 6 6 4 4 2 2 -2 -2 2 4 6 8 10 x -10 -8 -6 -4 -2 -2 -4 -4 -6 -6 -8 -8 Drawing a vertical line we see it may cross the graph in only one point so IT IS A FUNCION! 2 4 6 8 10 Drawing a vertical line we see it crosses the graph in TWO POINTS so it is NOT A FUNCTION x

Determine if the graphs below are functions? y -10 -8 -6 -4 y 10 10 8 8 6 6 4 4 2 2 -2 -2 2 4 6 8 10 x -10 -8 -6 -4 -2 -2 -4 -4 -6 -6 -8 -8 Drawing a vertical line we see it may cross the graph in only one point so IT IS A FUNCION! 2 4 6 8 10 Drawing a vertical line we see it crosses the graph in TWO POINTS so it is NOT A FUNCTION We will call this the VERTICAL LINE test. It will help us decide if a relation is a FUNCTION. x

Function Notation • By naming a function “f”, you can write the function using function notation: • The symbol f(x) is read a “the value of f at x” or simply “f of x”. • Note that f(x) is another name for y. • The input values for x are the domain of f. • The output values for f(x) or y are the range of f. • Function names could be represented by other names than f, such as g(x), or even names like abs(x) or sin(x).
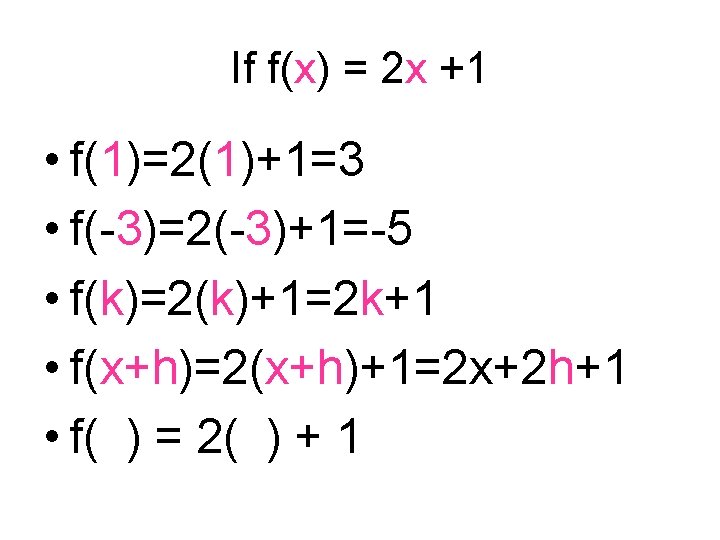
If f(x) = 2 x +1 • f(1)=2(1)+1=3 • f(-3)=2(-3)+1=-5 • f(k)=2(k)+1=2 k+1 • f(x+h)=2(x+h)+1=2 x+2 h+1 • f( ) = 2( ) + 1

Evaluate the following functions with the given values: g(x) = 2 x + 1 and g(3) = 2( 3 ) + 1 2 h(x)= 4 x -1 2 h(2) = 4( 2 ) -1 =6+1 = 4(4)-1 =7 = 16 -1 g(-5) = 2( -5 ) + 1 = -10 + 1 = -9 g(k) = 2( k) + 1 = 2 k + 1 g(r+1) = 2( r+1) + 1 = 2 r + 2 + 1 = 2 r + 3 =15 2 h(0) = 4( 0 ) -1 = 0 -1 =-1 2 h(z) = 4( z ) -1 = 4 z 2 -1

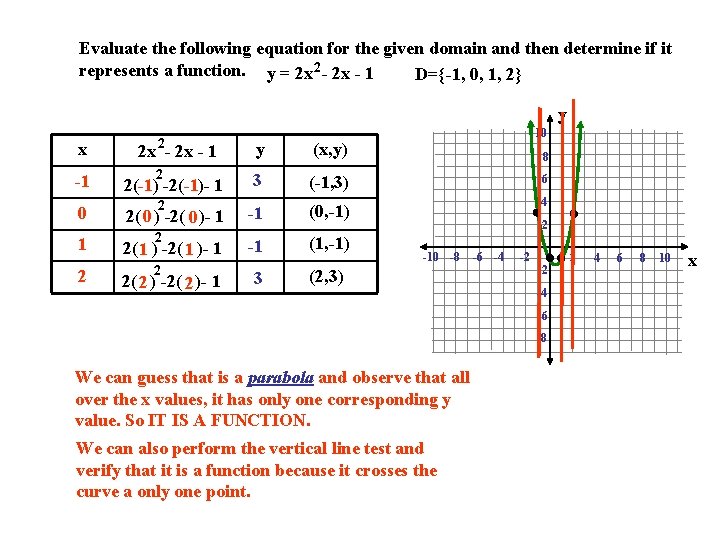
Evaluate the following equation for the given domain and then determine if it represents a function. y = 2 x 2 - 2 x - 1 D={-1, 0, 1, 2} y y (x, y) 2 3 (-1, 3) 6 2 -1 (0, -1) 4 -1 (1, -1) x 2 x - 1 -1 2(-1) -2(-1)- 1 0 1 2 10 2 2( 0 ) -2( 0 )- 1 2 2( 1 ) -2( 1 )- 1 2 2( 2 ) -2( 2 )- 1 3 8 2 -10 -8 (2, 3) -6 -4 -2 -2 -4 -6 -8 We can guess that is a parabola and observe that all over the x values, it has only one corresponding y value. So IT IS A FUNCTION. We can also perform the vertical line test and verify that it is a function because it crosses the curve a only one point. 2 4 6 8 10 x

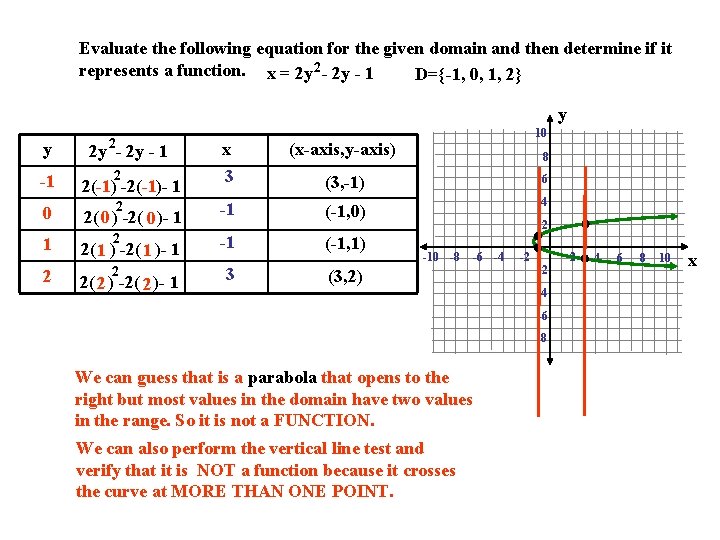
Evaluate the following equation for the given domain and then determine if it represents a function. x = 2 y 2 - 2 y - 1 D={-1, 0, 1, 2} y 2 y - 1 -1 2(-1) -2(-1)- 1 0 1 2 10 (x-axis, y-axis) 2 x 3 (3, -1) 6 2 -1 (-1, 0) 4 -1 (-1, 1) 2( 0 ) -2( 0 )- 1 2 2( 1 ) -2( 1 )- 1 2 2( 2 ) -2( 2 )- 1 3 8 2 -10 -8 -6 -4 (3, 2) -2 -2 -4 -6 -8 We can guess that is a parabola that opens to the right but most values in the domain have two values in the range. So it is not a FUNCTION. We can also perform the vertical line test and verify that it is NOT a function because it crosses the curve at MORE THAN ONE POINT. 2 4 6 8 10 x

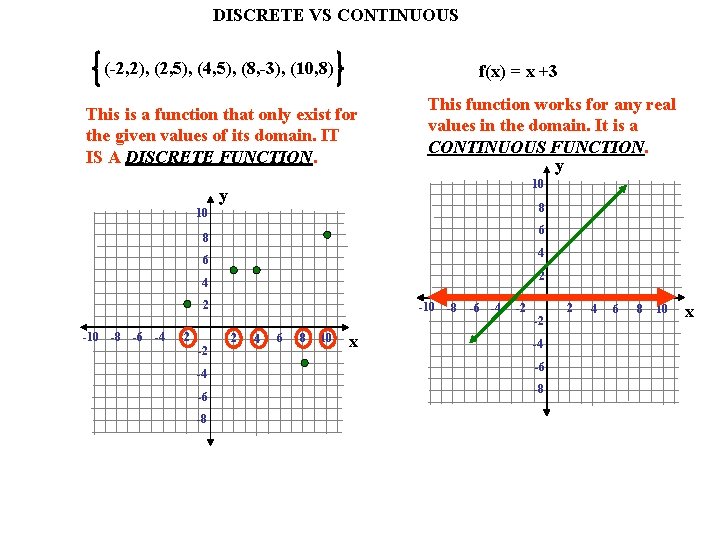
DISCRETE VS CONTINUOUS (-2, 2), (2, 5), (4, 5), (8, -3), (10, 8) f(x) = x +3 This is a function that only exist for the given values of its domain. IT IS A DISCRETE FUNCTION. This function works for any real values in the domain. It is a CONTINUOUS FUNCTION. y 10 y 8 10 6 8 4 6 2 4 2 -10 -8 -6 -4 -2 -2 -4 -6 -8 2 4 6 8 10 x

A function like f(x)=2 x+1 • • Is a called a linear function. Linear functions are of the form y=mx+b. m and b are constants. The graph of a linear function is a line.

LINEAR Functions (Equations) Linear equations: y 1 = 2 x 1+ 5 5 x-1 2 y 1 = 6 Not linear equation: 4 x 4– 3 x 3+ 2 x 2– 3 = y Exponents are different than 1. 5 x 1 = 2 x 1 + 5 2 x 1 - 4 = 4 y 1+ 6 1 4 b 1+ a = 10 y 1 = 10 All are one or two variable equations with exponents always 1.

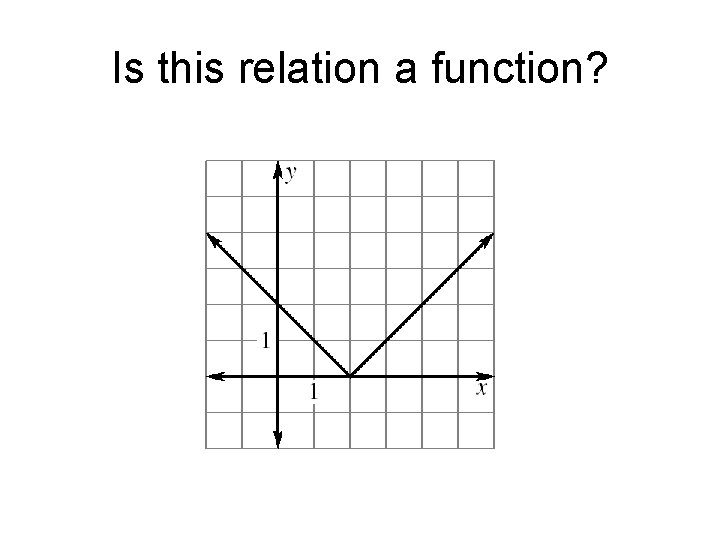
Is this relation a function?

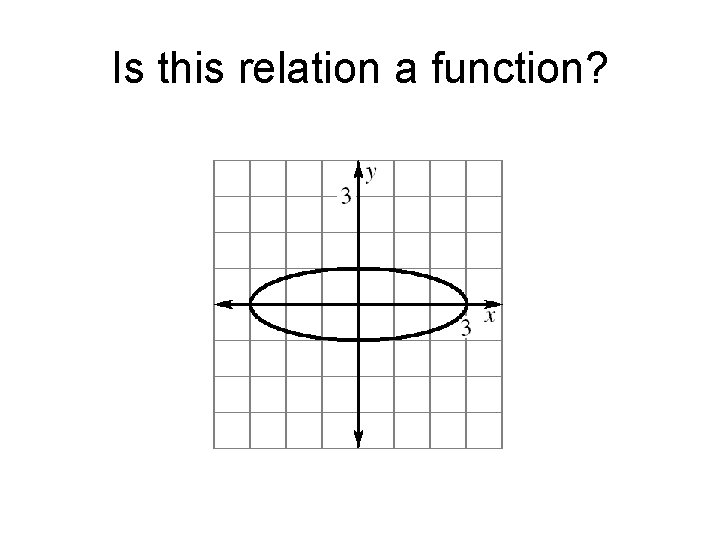
Is this relation a function?

Is this relation a function?

Is this relation a function?




Homework 17 -47 odd, 49, 52