2 1 Conditional Statements Goal 1 Recognizing Conditional

2. 1 Conditional Statements

Goal 1: Recognizing Conditional Statement l. A logical statement with 2 parts l 2 parts are called the hypothesis & conclusion l Can be written in “if-then” form; such as, “If…, then…” l Hypothesis is the part after the word “If” l Conclusion is the part after the word “then”

Ex: Underline the hypothesis & circle the conclusion. l If you are a brunette, then you have brown hair. hypothesis conclusion

Ex: Rewrite the statement in “if-then” form 1. Vertical angles are congruent. If there are 2 vertical angles, then they are congruent. If 2 angles are vertical, then they are congruent.

Ex: Rewrite the statement in “if-then” form 2. An object weighs one ton if it weighs 2000 lbs. If an object weighs 2000 lbs, then it weighs one ton.

Counterexample l Used to show a conditional statement is false. l It must keep the hypothesis true, but the conclusion false!

Ex: Find a counterexample to prove the statement is false. l If x 2=81, then x must equal 9. counterexample: x could be -9 because (-9)2=81, but x≠ 9.

Negation l Writing l Ex: the opposite of a statement. negate x=3 x≠ 3 l Ex: negate t>5 t 5

Converse l Switch the hypothesis & conclusion parts of a conditional statement. l Ex: Write the converse of “If you are a brunette, then you have brown hair. ” If you have brown hair, then you are a brunette.

Inverse l Negate the hypothesis & conclusion of a conditional statement. l Ex: Write the inverse of “If you are a brunette, then you have brown hair. ” If you are not a brunette, then you do not have brown hair.

Contrapositive l Negate, then switch the hypothesis & conclusion of a conditional statement (negate the converse) l Ex: Write the contrapositive of “If you are a brunette, then you have brown hair. ” If you do not have brown hair, then you are not a brunette.

Equivalent Statements – both are true or both are false. The original conditional statement & its contrapositive will always have the same meaning. The converse & inverse of a conditional statement will always have the same meaning.

Goal 2: Using Point, Line, and Plane Postulates Postulate 5: Through any 2 points, there exists exactly one line. Postulate 6: A line contains at least 2 points. Postulate 7: If two lines intersect, then their intersection is exactly one point. Postulate 8: Through any 3 noncollinear points, there exists exactly one plane. Postulate 9: A plane contains at least 3 noncollinear points. Postulate 10: If 2 points lie in a plane, then the line containing them lies in the plane. Postulate 11: If 2 planes intersect, then their intersection is a line.

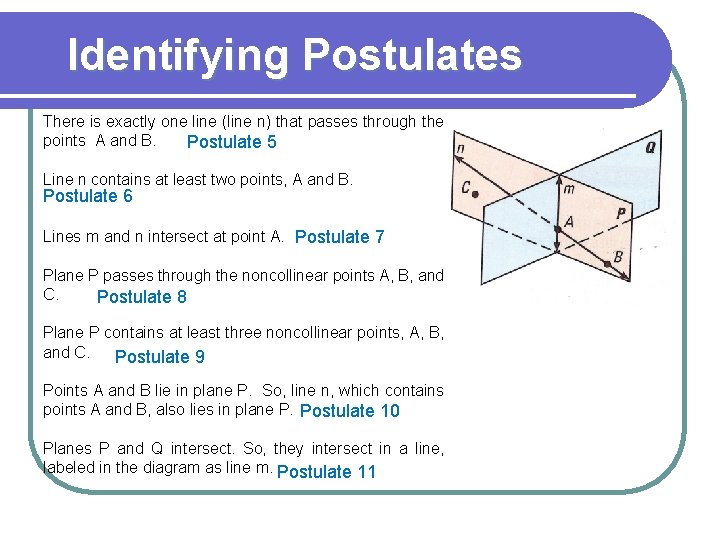
Identifying Postulates There is exactly one line (line n) that passes through the points A and B. Postulate 5 Line n contains at least two points, A and B. Postulate 6 Lines m and n intersect at point A. Postulate 7 Plane P passes through the noncollinear points A, B, and C. Postulate 8 Plane P contains at least three noncollinear points, A, B, and C. Postulate 9 Points A and B lie in plane P. So, line n, which contains points A and B, also lies in plane P. Postulate 10 Planes P and Q intersect. So, they intersect in a line, labeled in the diagram as line m. Postulate 11